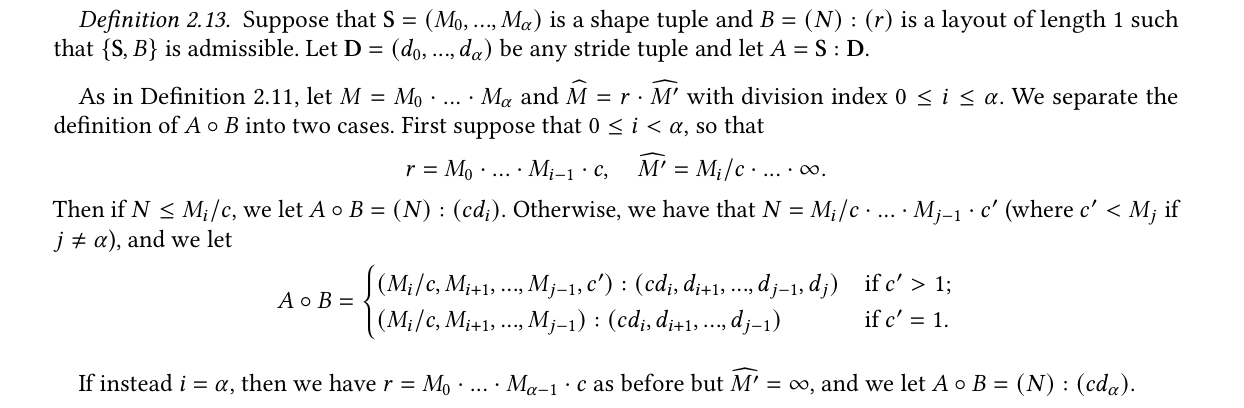Skip to content

CUTLASS CUTE 1 Layout Algebra

约 3941 个字 109 行代码 4 张图片 预计阅读时间 21 分钟

这是整个 cute 的核心，并且 cute 本身文档很难读，而且网上没有太多的学习资料，所以就算是 GPT 也很难给出好的回答。我的学习资料主要来源于三个部分：1. Reed zhihu 2. Lei Mao's blog 3. A note on the algebra of CuTe Layouts

我想以三个部分来介绍，目的是为了形成对 layout algebra 的清晰理解

  1. layout 基本概念
  2. layout algebra 基本运算
  3. layout algebra 组合运算

基本概念

layout 概念非常简单，就是由两部分组成：shape & stride，二者共同构建出一个整数到整数的映射：\(\mathbb{N} \rightarrow \mathbb{N}\)

\[ shape=(s_0,s_1,...,s_{n-1})\\ stride=(d_0,d_1,...,d_{n-1})\\ \]

为了完成这个映射，我还需要引入一个概念：整数与多维坐标的同构性 (isomorphism)。在数学上，两个东西同构意味着二者本质上是一个东西，二者可以通过一个映射进行可逆的转换。现在我们来构建整数与多维坐标的转换，就能够证明二者的同构性。我们定义多维坐标是 shape 空间中的一个点\((x_0,x_1,...,x_{n-1})\)，通过点积我们就能完成多维坐标到整数的转换

\[ x=f(x_0,x_1,...,x_{n-1}) = x_0·1+x_1s_0+...+x_{n-1}\prod_{i=0}^{n-2}s_{i} \]

而整数到多维坐标的转换则是通过取余完成

\[ f'(x)=\left( x \bmod s_0,\ \left\lfloor \frac{x}{s_0} \right\rfloor \bmod s_1,\ \ldots,\ \left\lfloor \frac{x}{s_0 \times \cdots \times s_{n-2}} \right\rfloor \bmod s_{n-1} \right) \]

实际上这就是列优先的顺序排列方式

Python
# shape (2, 3) with its int
(0,0)<->0      (0,1)<->2      (0,2)<->4
(1,0)<->1      (1,1)<->3      (1,2)<->5

有了以上的转换过后就可以定义 layout function 映射了，定义为如下

\[ Layout(x) = g(f'(x)) \]

其中\(f'(·)\)即为将整数转换为坐标的映射，而\(g(·)\)为将坐标转换为整数的映射，其本质是坐标 coord 与步长 stride 的点积

\[ g(x_0,x_1,...,x_{n-1})=coord ·stride=s_0d_0+s_1d_1+...+s_{n-1}d_{n-1}\\ \]

如此一来我们就完成了从整数到整数的映射：我们从整数\(x\)出发，寻找其对应的坐标点，然后通过步长进行新的映射

此时你可能发现了，将\(f\)与\(g\)其实非常相似，都是将坐标映射到整数。在之前我也提到了，\(f\)本身就是 column-major 的排列方式，其可用一个特殊的 layout 来表示，该 layout 我们称之为 layout left (or natural layout)

\[ shape=(s_0,s_1,...,s_{n-1})\\ stride=(d_0,d_1,...,d_{n-1})\\ d_i=\prod_{j=0}^{i-1}s_j=d_{i-1}s_{i-1},d_0=1 \]

举一个例子，一个 shape 为 (2, 3, 4) 的 natural layout 为

Python
Layout(shape=[2, 3], stride=[1, 2])
        0      2      4
        1      3      5

有了 layout left，那就有 layout right，也就是行主序排列

Python
Layout(shape=[2, 3], stride=[3, 1])
        0      1      2
        3      4      5

Layout 其中一个作用就是用来描述坐标与内存位置。这是很自然的事情，因为物理内存永远都是以一维的形式来表达，所以在 cutlass cute 中就是用一个指针 + 一个 layout 来描述一个 tensor，并且在 cutlass 中以 shape:stride 的形式 print layout

C++
Tensor(Ptr const& ptr, Layout const& layout)
Layout(shape=[2, 3], stride=[3, 1]) // (2, 3):(3, 1)

而实际上 Layout 可以用来描述更多的事情，例如：如何将一个\((M,N)\)形状 tensor 分配到\((T,V)\)形状当中。其中\(T\)就是 threads 数量，\(V\)是每一个 thread 拥有的 values，这将在基本运算小节中进行介绍

基本运算

layout algebra 最抽象的部分在于其基本运算，尤其是以下两个基本运算：

  1. complement，补运算
  2. compose，复合运算

当然还有其他的运算，例如 concat, coalecse，我用代码来简单解释

Python
"""
@dataclass
class Layout:
    shape: List[int]
    stride: List[int]
"""

A = Layout([2, 3], [1, 2])
B = Layout([4], [10])
coalesce(A) # Layout(shape=[6], stride=[1])
concat(A, B)# Layout(shape=[2, 3, 4], stride=[1, 2, 10])

concat 就是将 shape & stride 分别连接，而 coalecse 则是合并 shape & stride，以更少维度呈现

Complement

补运算需要两个元素，整数\(M\)和 layout 本身。我先用一个一维的例子来说明补运算的作用，这也是 reed zhihu 中所使用到的例子

Python
A = Layout([4], [2])
B = complement(8, A)    # Layout(shape=[2], stride=[1])

在 reed zhihu 中说到

当codomain存在不连续时，则存在空洞的位置，如图4所示，这时候我们可以构造一个Layout2能够填充上codomain的空洞位置，此时我们构造的Layout则为原Layout的补集

我认为 complement 的作用是计算出了 layout 所需要重复的“次数”以填满整个\(M\)空间。用上面的例子来说

Python
0 2 4 6
0 1 2 3 4 5 6 7

A 还需要重复两次才能够填满 0~8 的整个空间，而后面的 stride 则描述了重复空间之间的间隔，在这里间隔是 1。实际上只需要将 A 和 A 的补 concat 起来就会发现，二者组成了一个连续的空间

Python
C = concat(A, B)    # Layout([4, 2], [2, 1])

在这个 case 中 concat 过后的结果是一个 layout right 排布

再举一个二维的例子

Python
A = Layout([2, 3], [2, 4])
B = complement(24, A)   # Layout(shape=[2, 2], stride=[1, 12])

# Layout A
#     0      4      8
#     2      6     10

# Layout([4, 6], [1, 4])
#     0      4      8     12     16     20
#     1      5      9     13     17     21
#     2      6     10     14     18     22
#     3      7     11     15     19     23

可以看到 A 需要在两个维度（在 cutlass 中习惯把一个维度称之为一个 mode）的方向上都分别重复两次。在第一个 mode 上重复空间的间隔是 1，而在第二个 mode 重复空间的间隔是 12。我们仍然可以将 A 和 B 进行对应 mode 的 concat

Python
A = Layout([2, 3], [2, 4])
B = Layout([2, 2], [1, 12])
C = Layout([(2, 2), (3, 2)], [(2, 1), (4, 12)])

concat 之后的 Layout C 实际上可以看做一个合并的 Layout([4, 6], [1, 4])

现在我们再来看 complement 的公式就会发现其中的奥秘：

\[ \operatorname{complement}(A, M) = \left( d_{0},\ \frac{d_{1}}{s_{0}d_{0}},\ \frac{d_{2}}{s_{1}d_{1}},\ \cdots,\ \frac{M}{s_{a}d_{a}} \right) : \left( 1,\ s_0 d_{0},\ s_1 d_{1},\ \cdots,\ s_a d_{a} \right) \]

其本质就是在计算每一个 mode 还需要重复多少次才能够填满整个空间，重复空间的间隔即为子空间大小\(s_id_i\)

Compose

既然是映射（函数），那么将两个函数进行复合是再正常不过的想法了。从直观上来说将两个 layout 进行 compose 非常简单，毕竟都是整数到整数的映射：

\[ g_3=g_1(g_2(x)) \]

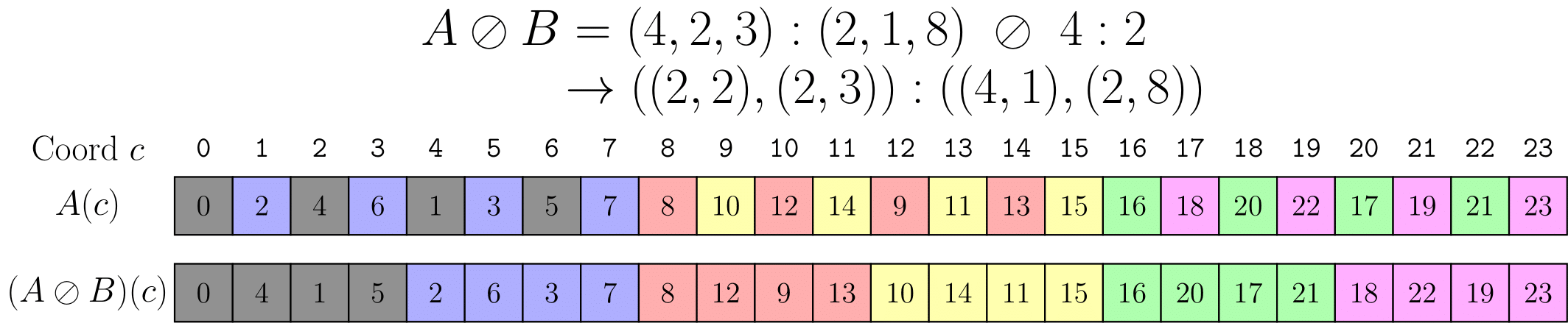
但是需要考虑的问题是，如何将新的 compose 结果\(g_3\)描述为一个合法的 layout 结构 (shape, stride)。而这个描述其实还是要化不少笔墨介绍的，这里省略，可参考 Definition 2.13 from A note on the algebra of CuTe Layouts

image-20250525152931437

NOTE: 其实 layout algebra 对于输入其实都是有要求的，并不是任意两个 layout 进行 compose 都是可行的，其对于整除性还是有不少要求。好消息是如果数值都是以\(2^n\)存在，整除性质就会得到很好的保障，而这正是在 GPU 编程中常用的数值。

虽然说需要严谨的数学来保证 compose admissibility，但这不妨碍其本质就是上述所说的复合函数，即：从一个 domain 映射到另一个 domain。我将以一个非常具体的例子帮助理解这个 compose 过程

Python
TV2MN = Layout([4, 2, 2], [2, 1, 8])
MN2Memory = Layout([4, 4], [4, 1])

首先我定义了两个 layout，第一个 TV2MN 描述了 thread values 所对应的 MN 映射。第二个 MN2Memory 描述了 MN 到内存的映射。更具体来说

  1. TV2MN 描述了 4 个线程，每一个线程拥有有 (2, 2) 个 values，这些 values 将映射到一个 shape 为 (M, N) 的 tensor 上。该 layout 也将描述 tensor 是如何被分配到线程当中的
  2. MN2Memory 描述了 tensor 中各个坐标的 value 在内存当中的位置。在例子当中是一个 layout right 的排布，也就 tensor 在内存中是行优先排列

通过 compose 我们可以直接获得 TV2Memory 这样的映射，该映射即代表了内存中的数据如何被分配到线程当中

Python
TV2Memory = compose(MN2Memory, TV2MN) # Layout(shape=[2, 2, 4], stride=[1, 8, 2])

我们将这个例子打印出来，通过 step by step 的方式看下整个 compose 的过程：

Python
TV2MN: Layout(shape=[4, 2, 2], stride=[2, 1, 8])
        0|     1|     8|     9|
        2      3     10     11
        4      5     12     13
        6      7     14     15
MN natural: Layout(shape=[4, 4], stride=[1, 4])
        0|     4      8|    12
        1|     5      9|    13
        2      6     10     14
        3      7     11     15
MN2Memory: Layout(shape=[4, 4], stride=[4, 1])
        0|     1      2|     3
        4|     5      6|     7
        8      9     10     11
    12     13     14     15
TV2Memory: Layout(shape=[2, 2, 2, 2], stride=[8, 1, 4, 2])
        0|     4|     2|     6|
        8     12     10     14
        1      5      3      7
        9     13     11     15

以 thread 0 为例：

  1. 其对应的 MN index 为 (0, 1, 8, 9)
  2. 通过 MN index 可以找到 (0, 1, 8, 9) 分别对应坐标 (0,0), (1,0), (0,2), (1,2)
  3. 通过对应坐标找到 MN2Memory 所对应的值为 (0, 4, 2, 6)
  4. 所以 thread 0 的 4 个 values 将会寻找内存中第 0, 4, 2, 6 个元素

由此我们就完成了一个映射，其从 TV domain 出发，映射到了 Memory domain。这也引出了 compose 的一个直观性质：不改变 source domain，即输入的 layout “形状”是不会改变的

Python
TV2MN: Layout(shape=[4, 2, 2], stride=[2, 1, 8])
TV2Memory: Layout(shape=[(2, 2) 2, 2], stride=[8, 1, 4, 2])

Inverse

同样的，在函数中也存在逆函数。在 layout algebra 中的逆函数定义可参考 reed-zhihu 中的 two line notation 表示形式。所谓的 two line 就是：input domain 为一个 line，output domain 为一个 line，下面举一个例子

Python
# Layout(shape=[2, 3], stride=[3, 1])
# [0, 1, 2]
# [3, 4, 5]

coord: [0, 1, 2, 3, 4, 5]
value: [0, 3, 1, 4, 2, 5]

# sort the pair according to value
coord: [0, 2, 4, 1, 3, 5]
value: [0, 1, 2, 3, 4, 5]

# switch coord and value as new layout
coord: [0, 1, 2, 3, 4, 5]
value: [0, 2, 4, 1, 3, 5]

上述 two line notation 用于理解 inverse 是比较直观的，但是对于理解 inverse 过后 layout 形式是怎么样的，没有太大帮助。具体来说，他们的 shape & stride 应该如何得到？在 Lei Mao's blog 当中证明了 compact layout inverse 过后的 shape & stride 应当如何计算，不过 blog 当中的叙述顺序对我来说略显晦涩，我这里用我自己的思考逻辑来整理

Conditions:

  • Layout function:\(f_L(x)\)

  • shape & stride 为\(S=(s_0,s_1,...,s_n),D=(d_0,d_1,...d_n)\)

  • natural layout funciton 将多维坐标\((x_0, x_1, ...,x_n)\)映射为\(x\)

    \[ x=x_0+x_1·s_0+...+x_n·\prod_0^{n-1}s_i \]

Target:

  • 找到 inverse layout:\(f_{L'}(x)\)使得满足

    \[ f_{L'}(f_L(x)) = x \]

  • inverse layout\(L'\)shape & stride 为\(S'=(s_0',s_1',...,s_n'),D'=(d_0',d_1',...d_n')\)

现在开始正式推导。对于输入\(x\)对应的\(L\)坐标为\((x_0, x_1, ..., x_n)\)，我们设其输出为\(x'\)

\[ f_L(x)=x' \]

输出\(x'\)所对应的\(L^{-1}\)坐标为\((x_1',x_2',...,x_n')\)，由\(L'\)shape 的 natural layout function 完成映射。由等式条件得

\[ \begin{aligned} f_{L'}(f_L(x)) &= f_{L'}(x') \\ &= f_{L'}(x_0',x_1',...,x_n') \\ &= x_0' \cdot d_0' + x_1' \cdot d_1' + \cdots + x_n' \cdot d_n' \\ &= x \\ &= x_0 + x_1 \cdot s_0 + \cdots + x_n \cdot \prod_{i=0}^{n-1} s_i \end{aligned} \]

其中最重要的等式为

\[ x_0' \cdot d_0' + x_1' \cdot d_1' + \cdots + x_n' \cdot d_n' =x_0 + x_1 \cdot s_0 + \cdots + x_n \cdot \prod_{i=0}^{n-1} s_i \]

下面的证明思路为：如果我们能够找到一个 permutation\(I=\{i_0,i_1,...,i_n\}\)，使得\(x_{i_0}'=x_0,x_{i_1}'=x_1,...,x_{i_n}'=x_n\)，那么我们就能对应多项式的每一项，直接算出每一个\(d'\)的值。现在我们来考察\((x_0,x_1,...,x_n)\)与\((x_0',x_1',...,x_n')\)之前的联系是什么，是否存在这样的 permutation

他们之间的关系非常清晰

\[ (x_0,x_1,\ldots,x_n) \xleftrightarrow{L} x' \xleftrightarrow{N} (x_0',x_1',\ldots,x_n') \]

这里的\(N\)就是 inverse layout 的 natural function。现在问题转换为：对于一组\((x_0,x_1,...,x_n)\)与\((x_0',x_1',...,x_n')\)，他们彼此都是对方的 permutation，我们需要找到合适的 natural layout function 即可。其实对于第一个要求非常好满足（忽略 natural layout 限制），我们可以直接对\(L\)中的 shape & stride 进行 permute 即可。以简单的 Layout(shape=[2,3], stride=[3,1]) 为例子，当 permute shape & stride 时，坐标也随之 permute

\[ (x_0,x_1) \xleftrightarrow{(2,3):(3,1)} x' \xleftrightarrow{(3,2):(1,3)} (x_1,x_0) \]

现在只需要考虑 natural layout 的限制即可，而答案也就随之浮出水面：只需要将\(L\)的 shape & stride permute 成为一个 natural layout (left layout) 即可。更具体来说，根据 stride 的大小，从小到大进行排列，由于 layout 有 compact 保证，没有任何空洞，所以排列出来的 layout 必定也是 natural layout。所以此 permutation 存在且唯一，确定了 inverse layout 的 shape，其对应的 stride 也可由下面的式子进行计算

\[ d_{i_0}'=1,\\ d_{i_1}'=s_0,\\ ...,\\ d_{i_n}'=\prod_{i=0}^{n-1} s_i,\\ \]

那么根据上述结论，我们就找到了\(L'\)的 shape & stride 了！其中 shape 的结论会很 clean，就是将\(L\)进行 sort 过后的 shape。从定性来说：原始 stride 小的 shape 在 inverse 过后会靠前；反之则会靠后

而在 写给大家看的 CuTe 教程：Layout compose & Inverse 中提到，通常 inverse 过后还会使用 with_shape 来构建我们期望的 layout shape，我们必须要了解 inverse 的输出形状到底是什么，才能正确地使用 with_shape。具体的例子在 retile 部分中，计算 (t, v) -> (m, n) layout 进行展示，其精妙地展示了 inverse 的一个核心作用：domain 的交换。如果我们获得了 (m, n) -> (t, v) 的映射，直接使用 inverse 就可以获得 (t, v) -> (m, n) 映射

组合运算

有了 layout algebra 所定义的基础运算就可以定义一些更复杂更有用的运算：divide & product

divide

divide 是划分数据中最常用的方法，尤其是 zipped divide。我先介绍 logical divide 的一维运算公式（B 是维度为1的 layout，A 没有限制）

Python
def logical_divide(A, B):
    M = A.size()
    c_B = complement(M, B)
    concatenated = concat(B, c_B)
    return compose(A, concatenated)

可以看到，其先计算了 B 补集，然后与 B 进行了 concat，最后用 concat 过后的 layout 与 A 进行了 compose。通常我们称 layout B 就是一个 Tiler，以 Tiler 为粒度对 A 进行了划分。在实际应用过程中都是对一个 layout 进行逐维度 divide (by-mode divide)

C++
Layout Shape : (M, N, L, ...)
Tiler Shape  : <TileM, TileN>

logical_divide : ((TileM,RestM), (TileN,RestN), L, ...)
zipped_divide  : ((TileM,TileN), (RestM,RestN,L,...))

divide1.png

在上面的例子中 Tiler 是不连续的，而我们更常会遇到的 Tiler 是最简单的 stride 为 1 的 Tiler。如 B = Layout([4], [1])，这样就会以 4 为单位切分该轴。zipped divide 会将 Tiler 维度直接提到最前面来，以方便我们进行索引操作，通常这个维度可以是 thread，这样通过索引就获得具体某个线程所对应的数据

通常我们遇到的情况都是：A & B 都是 1-dim，如果 A 为多维 layout，那么就需要谨慎看待，最后的结果一般不是我们想要的。举个例子

Python
l1 = Layout([5, 4], [1, 30])
l2 = Layout([4], [1])
# logical_divide(l1, l2) won't work
A size: 20
complement of B: Layout(shape=[5], stride=[4])
concated (B, c_B): Layout(shape=[4, 5], stride=[1, 4])

原因在于 concated layout 无法和 A 进行 compose。不过好消息是在进行数据 divide 时，通常是对 MN shape 进行 divide，这是一个非常规整的 domain，满足我们在 by-mode divide 时各个 mode dim 都是 1 的需求

product

这里有个割裂感：我们说 product 为 divide 的逆运算，但实际上我发现二者并不能进行可逆操作。例如 C != A.product(B).div(B)。但是这个定义并不符合我们的直觉，严谨的数学定义在 Lei Mao's blog 中有所阐述。这里以一个 2D exmaple 作为说明

image-20251027162320196

这个 product 的结果非常直观：把 (2, 5): (5, 1) 进行重复，重复维度为 (3, 4)。在我的期望中，直接使用 tiler <3:1, 4:1> 就能完成上述功能，但实际上用的 tiler 为 <3:5, 4:6>，这就是因为 product 的定义并不是我们想象中的直观，仍然是根据 complement & compose 来定义的。为了让 product 功能与我们的编程直觉相符，cute 直接构建了几种常见的 api 方便调用，参考 reed zhihu

乘法模式 乘积的shape
logical ((x, y), (z, w))
zipped ((x, y), (z, w))
tiled ((x, y), z, w)
blocked ((x, z), (y, w))
raked ((z, x), (w, y))

上面只列举了 shape，对于 stride 而言，相同 dimension 的 stride 也是一样的：即任意乘法模式中所有 x 对应的 stride 都一样。需要注意的是，这些操作是 layout x layout，而不是 layout x tiler。所以他们都是 rank sensitive 的，即两个 layout 的维度必须一致。同时和 divide 一样，通常使用在相对规整的 domain，即 layout 的 size 和 cosize 一致。否则存在空洞的话，product 也可能无法进行，举一个例子

C++
auto l1 = make_layout(make_shape(_4{}, _5{}), make_stride(Int<30>{}, _1{}));
auto l2 = make_layout(make_shape(_2{}, _4{}));
// can't do logical_product(l1, l2)

这里点出一个 product 和 divide 的重要差异：divide 习惯使用 layout divide tiler，而 product 习惯使用 layout product layout。另外一个实验是，product 的顺序是会改变结果的

C++
auto base_layout = make_layout(make_shape(_4{}, _3{}), make_stride(_4{}, _1{}));
auto layout_x2 = blocked_product(base_layout, make_layout(make_shape(_1{}, _2{})));
auto layout_x2_x2 = blocked_product(layout_x2, make_layout(make_shape(_2{}, _1{})));
auto layout_x4 = blocked_product(base_layout, make_layout(make_shape(_2{}, _2{})));

// Product order test
// ((_4,_1),(_3,_2)):((_4,_0),(_1,_16))
// (((_4,_1),_2),((_3,_2),_1)):(((_4,_0),_32),((_1,_16),_0))
// ((_4,_2),(_3,_2)):((_4,_16),(_1,_32))

我先对 base layout 在第二个 dim 进行扩张，然后再对第一个维度进行扩张，其结果和同时扩张两个维度是不一致的。在之后的内容当中，我们可以使用组合运算和基础运算来获得所需的 layout 排布，在实践中学习