CUTLASS CUTE 2 MMA & COPY 抽象¶

2025-12-242025-12-24

MMA¶

MMA Atom¶

mma atom 可以大致认为由两个部分组成：mma op & mma traits

1. MMA op 用于描述所使用的 PTX 命令，以及该命令所需要的寄存器

2. MMA traits 用于描述需要完成一个 MMA 所缺失的部分：包含数据类型、数据形状，线程数据排布 tv layouts

以 mma op SM80_16x8x16_F16F16F16F16_TN 为例来说明

// MMA 16x8x16 TN
struct SM80_16x8x16_F16F16F16F16_TN
{
    using DRegisters = uint32_t[2];
    using ARegisters = uint32_t[4];
    using BRegisters = uint32_t[2];
    using CRegisters = uint32_t[2];

    CUTE_HOST_DEVICE static void
    fma(uint32_t      & d0, uint32_t      & d1,
        uint32_t const& a0, uint32_t const& a1, uint32_t const& a2, uint32_t const& a3,
        uint32_t const& b0, uint32_t const& b1,
        uint32_t const& c0, uint32_t const& c1)
    {
#if defined(CUTE_ARCH_MMA_SM80_ENABLED)
    asm volatile(
        "mma.sync.aligned.m16n8k16.row.col.f16.f16.f16.f16 "
        "{%0,  %1},"
        "{%2,  %3,  %4,  %5},"
        "{%6,  %7},"
        "{%8,  %9};\n"
        : "=r"(d0), "=r"(d1)
        :  "r"(a0),  "r"(a1),  "r"(a2),  "r"(a3),
            "r"(b0),  "r"(b1),
            "r"(c0),  "r"(c1));
#else
    CUTE_RUNTIME_ASSERT("Attempting to use SM80_16x8x16_F16F16F16F16_TN without CUTE_ARCH_MMA_SM80_ENABLED");
#endif
    }
};

该 mma op 就是用来封装 PTX 接口的，给出所使用的命令以及该命令需要的寄存器。该 PTX 命令是一个 16x8x16 的矩阵乘，对应的数据类型都是浮点，而 TN 代表的是 transposed & normal，分别代表 row-major & col-major。需要强调两点：

1. 是 TN 并不是代表矩阵 A & B 他们的数据排布就是 row-major & col-major，这其实只是 PTX 遵循 BLAS 当中的语言约定。而真实的 A & B 数据排布，参考 TN & NT & TT & NN，TN 其实都是 row-major。并且输出的 C 也是 row-major
2. PTX 命令名字虽然包含了矩阵形状以及数据类型，但是只是名字，实际上在 mma op 中并不具体包含这些信息，所以仍需要 mma traits 提供

接下来看该 mma op 对应的 mma traits

template <>
struct MMA_Traits<SM80_16x8x16_F16F16F16F16_TN>
{
    using ValTypeD = half_t;
    using ValTypeA = half_t;
    using ValTypeB = half_t;
    using ValTypeC = half_t;

    using Shape_MNK = Shape<_16,_8,_16>;
    using ThrID   = Layout<_32>;
    using ALayout = Layout<Shape <Shape < _4,_8>,Shape < _2,_2,  _2>>,
                            Stride<Stride<_32,_1>,Stride<_16,_8,_128>>>;
    using BLayout = Layout<Shape <Shape < _4,_8>,Shape <_2, _2>>,
                            Stride<Stride<_16,_1>,Stride<_8,_64>>>;
    using CLayout = SM80_16x8_Row;
};

正如我之前所说，mma traits 提供了：数据类型 (val type)、数据形状 (shape mnk)、线程数据排布 (thread id, ABC layout)

线程排布其实就是 tv layouts，描述的 (threads, values) -> MK 的映射关系，在 reed zhihu 中用更详细的注释说明：

using ALayout =      // (Logical thread id (tid), Logical value id (vid)) -> Flat MK-coord
using BLayout =      // (Logical thread id (tid), Logical value id (vid)) -> Flat NK-coord
using CLayout =      // (Logical thread id (tid), Logical value id (vid)) -> Flat MN-coord

TiledMMA¶

mma atom 提供了一个 warp 所能完成的矩阵乘大小，通常我们会在一个 block 中使用更多的 threads，将多个 mma atom 组成一个 tiled mma。该组合通过参数 AtomLayoutMNK 来定义 atom 在 MNK 方向上重复的次数。

    static constexpr int kMmaEURepeatM = 2;
    static constexpr int kMmaEURepeatN = 2;
    static constexpr int kMmaEURepeatK = 1;
    using MMA_EU_RepeatT = decltype(make_layout(make_shape(Int<kMmaEURepeatM>{}, Int<kMmaEURepeatN>{}, Int<kMmaEURepeatK>{})));
    using MMA = decltype(make_tiled_mma(mma_atom{}, MMA_EU_RepeatT{});

上述代码在 MN 方向上重复了两次，于是从原来的 16x8x16 变为了 32x16x16 的矩阵乘

NOTE：绝大多数的情况下，都是在 MN 方向上重复 mma atom，几乎从来不会在 K 方向上重复 mma atom [QST] TiledMMA with >1 Atoms in K dimension --- how to reduce?。这其实是合理的，在 MN 方向上的重复可以通过简单的 atom 重复完成，而 K 方向上的重复需要进行额外的累加：即需要将多个重复的 mma atom 结果进行累加。通常在 K 方向的累加是通过 main loop 完成

另外还有一个参数 PermutationMNK，该参数是比较迷惑的，对于该参数的解释最终都会回到 [QST] What is PermutationMNK in TiledMMA in CUTLASS 3.4 changes?。其中对 PermuationMNK 最本质的介绍是：

The easiest way to think about it is that the Permutation parameter is a Tiler for the MNK modes of the MMA.

我先举一个实际例子说明其功能，再总结一下其影响

    // mma atom shape is 16x8x16
    using mma_atom_shape = mma_traits::Shape_MNK;
    static constexpr int kMmaPM = 1 * kMmaEURepeatM * get<0>(mma_atom_shape{});
    static constexpr int kMmaPN = 2 * kMmaEURepeatN * get<1>(mma_atom_shape{});
    static constexpr int kMmaPK = 1 * kMmaEURepeatK * get<2>(mma_atom_shape{});
    using MMA_P_T = Tile<Int<kMmaPM>, Int<kMmaPN>, Int<kMmaPK>>;
    using MMA = decltype(make_tiled_mma(mma_atom{}, MMA_EU_RepeatT{}, MMA_P_T{}));

这里 MMA_P_T 就是 PermutationMNK，在例子中的具体值为 M=(16x2), N=(8x2x2), K=(16)，即 32x32x16。由此就形成了一个 32x32x16 的 Tiler，会将输入数据按照这个 Tiler 形状进行分割。可以看到我们在 AtomLayoutMNK 重复的基础上，再对 N 方向又扩大了一倍

该参数有两个功能：

1. 对数据进行 permute，影响 data partition 结果（现在基本不使用该功能）

   如果 tiler 中某一个维度使用了特殊的 layout 例如 Layout<Shape <_2,_4,_4>, Stride<_1,_8,_2>>，这将会对数据进行重新的排布。但并不会影响最终的矩阵乘结果，因为 permutation 不改变 reduction 结果，并且最后数据在 copy 的过程中也会回到 permutation 之前的位置

2. 影响 get_layoutA/B/C_TV & tile_size。不影响 data partition 结果

   该功能用于扩大 tiler size 以增加 A/B/C tv layouts 中的 v size，从而满足 tiled copy 对 v size 的要求（这一句话高度抽象，一定要配合之后对 tiled copy 的学习）。简单来说，有的 mma atom tv layouts 中，size of v 为 4，即每一个线程分配 4 个 values；而 ldmatrix copy atom 会要求 size of v 至少为 8。在此情形下，直接使用 mma tv layouts 将不会满足要求，而需要增加 v size，该需求就是利用 PermutationMNK 扩大 MN shape 而满足的

ThrMMA¶

thread mma 的作用是根据 tiled mma 中所定义的 block tv layouts & mnk shape 对 tensor 进行划分（这里我忽略 permuationMNK 所带来的数据排布影响），获得每一个线程所需要的数据。对于一个 tensor shape (M, N)，使用 thread mma 按照 matrix A 的 tv layouts & mn shape 对 tensor 划分过后得到每个线程的 tensor shape 为：

第一个维度 num_v 代表了 block tv layouts 当中每一个 thread 控制的 values 数量，而 num_M 和 num_N 则代表 tensor 中的的 M & N 在各自维度上包含了多少个 atom。以上述 tiled mma 为例子，matrix B block tv layouts 中每一个 thread 有 4 个 values，nk shape 为 (16, 16) = (8x2, 16)，所以如果我们给定一个 tensor shape 为 (128, 32) 的话，得到的 thread tensor shape 为 (4, 8, 2) = (4, 128/16, 32/16)

ThrMMA 的作用仅限于划分，最终传入 cute::gemm 方法的仍然是 TiledMMA

Copy¶

copy 其实是比 mma 更加灵活更加复杂的操作。因为其要考虑到不同的硬件结构 (global memory, shared memory, register)，以及 source & destination 对于数据排布不同的要求。GPU 编程的魅力之一就在于如何搬运大量数据以增加数据吞吐量

Copy Atom¶

copy atom 我认为由三个部分组成：copy op, copy traits, copy type。

1. copy op 用于描述 PTX 指令以及所需的寄存器
2. copy traits 用于描述 src & dst tv layouts，以及线程数量。这里的 tv layouts 区别于 mma atom，其映射的 domain 不是矩阵的 shape，而是 bits，在实际使用过程中实际上是提供的数据的逻辑位置。这在之后的 ldmatrix/tiled copy 小节中将具体表现
3. copy type 表示数据类型

相比于 mma traits，copy traits 不一定是以 warp 单位来定义，即 tv layouts 中的 t 大小不一定是 32。我对此有一些疑问：难道 GPU 不都应该以 warp 为单位来执行吗？看来我将执行单元和内存操作的最小单位混淆了，二者应当区分看待

From DeepSeek

Warp 是执行单元，但不是内存操作的最小单位。确实，warp（32线程）是 GPU 的基本执行单元，但内存操作的最小单位不一定与 warp 对齐。这些指令可以由单个线程发起（虽然通常整个 warp 会协同工作）支持各种大小和模式

下面就是一个具体的 copy atom 及其对应 copy traits 在实际代码中的使用

    using T = cute::half_t;
    using g2s_copy_op = SM80_CP_ASYNC_CACHEGLOBAL<cute::uint128_t>;
    using g2s_copy_traits = Copy_Traits<g2s_copy_op>;
    using g2s_copy_atom = Copy_Atom<g2s_copy_traits, T>;

这里创建了一个 global to shared memory 的 copy atom，每一个 copy atom 可以完成一个 128bit 的数据搬运，由于我们使用的数据类型为半精度 16bit，所以一次将搬运 8 个数据元素

TiledCopy¶

同样的，和 tiled mma 一样，我们在一个 block 当中通常会有多个 threads，我们仍然需要对 copy atom 进行排布，组成一个更大的 tiled copy。下面就是一个创建 tiled copy 的例子

    // Each Tile will copy 32x32 half_t elements
    using G2SCopyA = decltype(make_tiled_copy(g2s_copy_atom{},
                                            make_layout(make_shape(Int<32>{}, Int<4>{}),
                                                        make_stride(Int<4>{}, Int<1>{})),
                                            make_layout(make_shape(Int<1>{}, Int<8>{}))));
    using G2SCopyB = G2SCopyA;

该 tiled copy 负责将 A & B 矩阵从 global memory 复制到 shared memory，每一次 copy 的 mn shape 为 (32, 32)。我想从 make_tiled_copy 的具体实现来看下传入参数的含义，我认为非常巧妙

make_tiled_copy(Copy_Atom<Args...> const& copy_atom,
                ThrLayout          const& thr_layout = {},     // (m,n) -> thr_idx
                ValLayout          const& val_layout = {})     // (m,n) -> val_idx
{
    // Take the raked_products to compute the Layout_MN
    // (M,N) -> (thr_idx, val_idx)
    auto layout_mn = raked_product(thr_layout, val_layout);
    // (thr_idx, val_idx) -> (M,N)
    auto layout_tv = right_inverse(layout_mn).with_shape(make_shape(size(thr_layout), size(val_layout)));
    // Tiler for extracting relevant elements
    // (M,N) -> tensor coord
    auto tiler = product_each(shape(layout_mn));
    return make_tiled_copy_impl(copy_atom, layout_tv, tiler);
}

可以看到在构造 tiled copy 中我们传入了两个 layout，一个是 thr_layout，另一个是 val_layout，我在一开始看到这两个 layout 的时候，只是单纯地觉得这就是在描述 thread 和 values 的排布，然后把这两个 layout 乘起来就获得了一个 (32, 32) 的 layout，正好就是 tiled copy 所覆盖的 tensor 区域，并且我错误地认为了这是一个 tv -> mn 的映射。而实际上这两个 layout 在描述 (m=32, n=4) -> tid 和 (m=1, n=8) -> vid 的映射，通过 raked product 进行了 interleaved 重复获得了 (m, n) -> (tid, vid) 的映射。所谓 interleaved 重复即为：在第二个维度是将 8 重复 4 次，而不是将 4 重复 8 次。这在实际的映射中表现为，在 n 方向会先看到同一个 thread 所拥有的连续 values，而不是同一个 value 的连续 thread。最后通过 right inverse 将映射返回成为 (tid, vid) -> (m, n)

auto l = Layout<Shape<_32, _4>, Stride<_4, _1>>{};
auto tiler = Layout<Shape<_2, _8>, Stride<_8, _1>>{};
auto lxtiler = logical_product(l, tiler);
auto lxtiler_rake = raked_product(l, tiler);

((_32,_4),(_2,_8)):((_4,_1),(_1024,_128))
((_2,_32),(_8,_4)):((_1024,_4),(_128,_1))

可以看到 make_tiled_copy 中还有一个 make_tiled_copy_impl，这个函数接受了两个参数 layout_tv 以及其对应的 tiler，他们二者就共同描述了 tiled copy 如何去划分一个 tiler 大小的数据，然后进行 copy。在实践过程中这个 layout_tv 通常可以是 tiled mma 中的 get_layoutA/B/C_TV，而 tiler 大小就是 PermutationMNK 所设置的 tiler size 大小

在上述例子当中只需要一个 block 进行一次 copy 就能够完成 (32, 32) 大小的 copy 任务。还有一种情况，一个 tiled copy 需要一个 block 进行多次来完成 (32, 32) 大小的 copy 任务，例如将上述例子中的 copy atom 换为 Copy_Atom<UniversalCopy<cute::uint32_t>, T>，一个线程只会复制两个 fp16 元素，此时 128 个线程只能够复制 256 个 fp16 元素，很明显并不能够一次完成 (32, 32) 大小的 copy 任务。所以一个 tiled copy 会执行多次来完成该 copy 任务

ThrCopy¶

利用 tiled copy 当中的 tiled tv layout & mn shape 对 tensor (M, N) 进行划分，得到每一个线程所拥有的 tensor，表达公式其实和 ThrMMA 是一样的

但不一样的是 num_V 不一定就是 copy atom 中的 values 数量，还可能是由于 tiled copy 会重复多次执行 copy atom 所导致的 num_V 的增加

ThrCopy 的作用仅限于划分， 最终传入 cute::copy 方法的仍然是 TiledCopy

ldmatrix¶

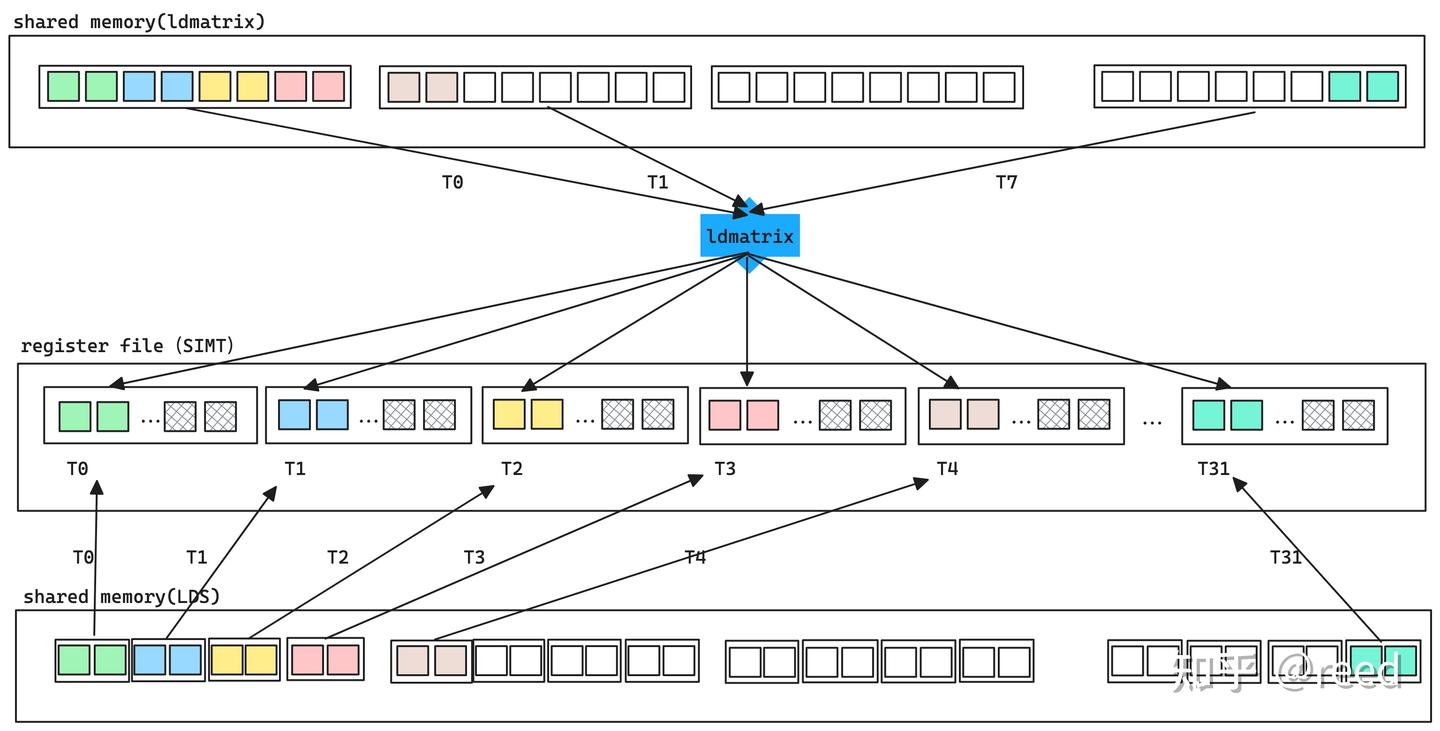
ldmatrix 是为了满足 mma atom 的特殊排布应运而生，ldmatrix 能够将自己线程的数据发送到其他线程当中，这在常规的 CUDA 编程中是做不到的，因为在 SIMT 编程下我们认为寄存器是线程私有的。

第一张图描述了 ldmatrix 的高效性：一个 thread 将搬运 8 个元素，并分配到不同的线程当中。在一般的 LDS 命令下，一个 thread 只能搬运 2 个元素，所以要进行 4 次搬运，效率大大降低。

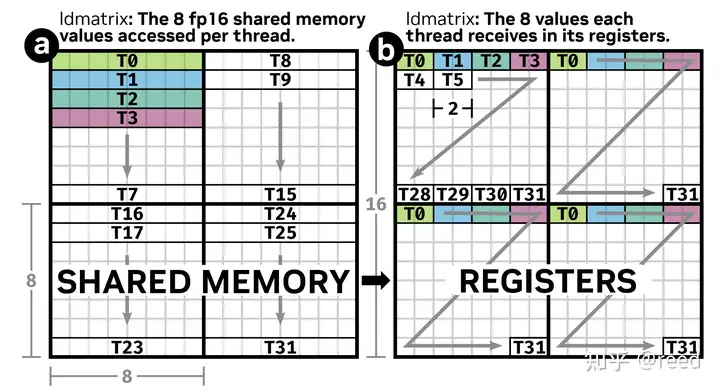
第二张图则需要对应我们的 copy traits 一起食用。该图其实就是 ldmatrix 的 warp 版本。其搬运了一个 (16, 16) 大小的 half 矩阵。需要注意的是数据排布顺序要按照图示中的箭头来看

template <>
struct Copy_Traits<SM75_U32x4_LDSM_N>
{
    // Logical thread id to thread idx (warp)
    using ThrID = Layout<_32>;

    // Map from (src-thr,src-val) to bit
    using SrcLayout = Layout<Shape < _32,_128>,
                            Stride<_128,  _1>>;
    // Map from (dst-thr,dst-val) to bit
    using DstLayout = Layout<Shape <_32,Shape <_32,   _4>>,
                            Stride<_32,Stride< _1,_1024>>>;

    // Reference map from (thr,val) to bit
    using RefLayout = DstLayout;
};

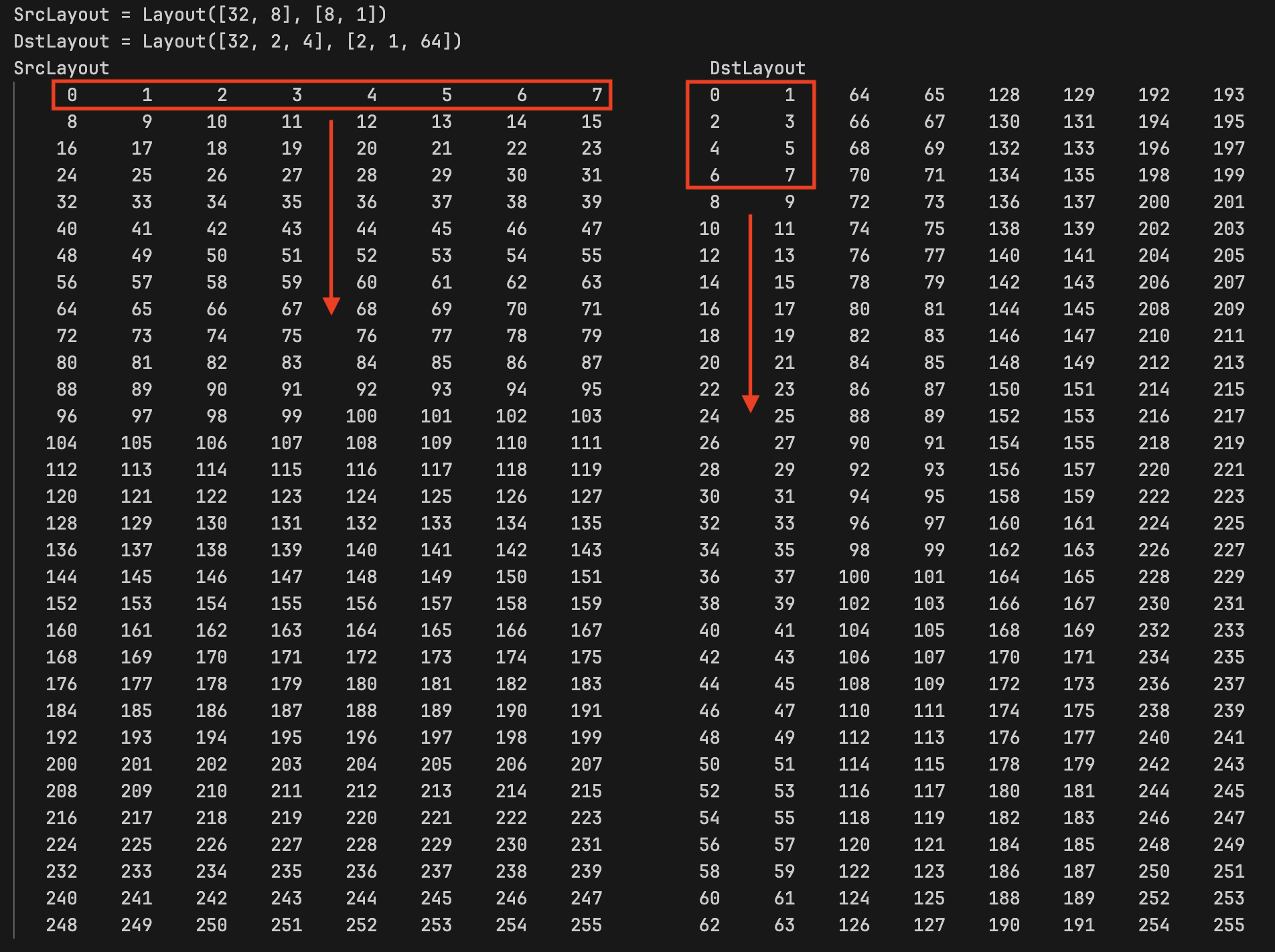
我们把 src layout 和 dst layout 都打出来看，由于所使用的 data type 为 half，所以 src layout 和 dst layout 转化为 (t, v) -> logical mem id 映射

上面的打印中相同的数字代表了相同的 logical mem id，即他们代表了统一个元素。可以看到在 src 当中的 t0 拥有数据 0~7，他们分别分配到了 dst 当中的 t0~t3 中的前两个 values 当中。而对于 dst 当中的 t0 数据则来自于 t0, t8, t16, t24 的前两个 values

为什么我始终强调逻辑位置 logical mem id，这是因为这些元素在内存中的位置与逻辑位置并不一致。最重要的是：根据 logical memory id 我们可以构建一个 src tv -> dst tv 的映射关系，从而能够轻松获得 src tv 中的元素在 dst tv 当中的位置

How to build?¶

构建 tiled copy 的双核心逻辑

1. 对于使用 universal copy 的场景，直接使用 make_tiled_copy 构建所需的 mn shape，从而直接定义一个 cta block 的 copy 能力

2. 对于 tv layouts 有特殊要求的 copy 场景（e.g. mma），此时需要考虑的是 tv layouts 与 copy atom 之间的合法性问题，即 copy atom 的整除要求（size of v 需要至少为 8）。此时一个 cta block 的 copy 能力是 mma atom mn shape 的重复，可通过 permutation mnk 参数进行调整

   对于 sm90 之后该问题不用考虑，mma 与 copy 之间的合法性总是能够得到满足，我们无需考虑 mma atom 需要重复几次以满足 copy 要求，只需要关注 cta tile 与 mma atom 之间的整除关系是否满足即可

考虑好了以上两个核心逻辑就可以清晰地计算 tiled copy 中的三个核心参数：copy atom, tiled tv layout, mn shape

此时一个大的 picture 正在浮现开来：tile centric CUDA programming。核心问题：What kinds of tile you want to choose to solve a cta problem?

对于 smem -> rmem 这个环节当中，我们利用 mma atom mn shape 作为基础的 building block，为了配合 copy atom 合法性，我们对其 mnk tile 进行了相应的重复，最终构建出实际使用的 mnk tile，cta problem 将由这个 tile 进行切分解决