Skip to content

CUTLASS CUTE 3 重要补充材料

约 2639 个字 50 行代码 3 张图片 预计阅读时间 14 分钟

retile 到底要解决一个什么样的问题？

结论：解决线程 register 的 layout 转换问题

我们在思考 copy 的问题时，其实还是更容易从整体去思考，例如把一个 MN shape 的数据进行划分，每一个线程获得各自的数据，然而最后我们都是面向 thread 编程，各个线程的 register 数据都是各自独立（互不可见）的，我们必须要将自己的视角进行转换。以下有三个划分视角：

对于一个 MN shape 数据

  1. 我们可以使用 mma atom 的 layout 对 MN shape 的数据进行划分，每一个线程的数据 tCrC_0

    假设 mma atom layout 的 mn shape 为 (m, n)，每一个 thread 有 4 个 values，那么 tCrC_0.shape = (4, M//m, N//n)

  2. 我们可以使用 s2r copy atom 的 layout 对 MN shape 的数据进行划分，每一个线程的数据 tCrC_1

    假设 s2r copy atom 的 mn shape 为 (2m, n)，每一个 thread 有 8 个 values，那么 tCrC_1.shape = (8, M//2m, N//n)

  3. 我们可以使用 r2s copy atom 的 layout 对 MN shape 的数据进行划分，每一个线程的数据为 tCrC_2

    假设 r2s copy atom 的 mn shape 为 (m, 2n)，每一个 thread 有 8 个 values，那么 tCrC_1.shape = (8, M//m, N//2n)

以上三种划分，最终得到了三种数据 tCrC_0/1/2，而这三种数据实际上包含了相同的数据内容，更具体来说，这三个 tensor 的 tensor.data()，指向的是同一片内存，但是他们的排布 tensor.layout() 完全不同。实际上 retile 干的事情就是这样，把相同拥有相同 data 的 tensor 转换为所需要的 layout，本质上就是做了这么一件事

C++
// retile A tensor to B tensor's layout
A_retiled = make_tensor(A.data(), B.layout())

但是这个 B 的 layout 计算有时候并不是那么明显的，所以 retile 将 B layout 计算都隐藏起来了。拥有了 retile 过后，就能够在各个形态进行丝滑转换，我们无论是在进行 mma 计算，还是在进行数据 copy，就可以构建同一份 register 数据的不同排布，以确保在 cute::copy & cute::gemm 在进行坐标 index 的时候获得了正确的数据

我之前对于 retile & tiled copy 没有那么熟，所以认为要用更多的概念来进行区分。实际上从始至终，我们都是在 block level 上进行编程，更多由重复所带来的功能，都可以由 cute::gemm & cute::copy 进行完成。而由于 copy & mma block 之间，对数据的划分各有不同，所以产生了对数据 layout 的操作转换，这带来了极大的学习困难

retile solved by compose & inverse

写给大家看的 CuTe 教程：Layout compose & Inverse 受到其中的例子启发，我又重新审视了一下 retile，并且更深入地对 product/divide 和 inverse 进行了练习，获得了一些不错的经验。现在对 retile 问题进行更具体的阐述：

Condition：对于一个 gmem tensor x，使用了两种 partition 方式（e.g. 不一样大小的 tiler），partition_A & partition_C，划分过后每个线程所获得的数据分别为 gA 和 gC，并且已经申请了 register rA = make_fragment_like<AType>(gA) 用于 copy gA

Target：以最小代价构建 rC

有三个不一样的思路（包含错误思路），我都来分析一下：

  1. 直接使用 gC 的 shape 和 rA 的数据

    C++
    rC = make_tensor(rA.data(), make_layout(gC.shape()))

    这显然是行不通的，gC shape 所生成的 layout 是一个 natural layout，其 stride 和真正的 rC 是不一样的

  2. 使用 make_fragment_like 构建 rC

    C++
    rC = make_fragment_like<AType>(gC)

    该方法的确能够获得正确的 rC layout，但是会额外申请寄存器，造成资源浪费。如果我们知道 make_fragment_like 计算 rC layout 的方法也是可行的

  3. 构建 gC coord -> gA coord 的映射，利用 compose 获得 rC coord -> offset 映射，该映射即为正确的 rC layout

    首先我们来看几个 tensor layout 所代表的映射

    • gA layout 是 gA coord -> gmem offset，即 tensor coordinate 到 gmem offset 的映射
    • gC layout 是 gC coord -> gmem offset，类似 gA
    • rA layout 是 rA coord -> rmem offset，即 tensor coordinate 到 register offset 的映射，其中 rA 的 shape 和 gA 是一致的
    • rC layout 是 rC coord -> rmem offset，类似 rA

    我们构建 gC coord -> gA coord 的桥梁就是：gA & gC 有着相同的 gmem offset domain，即他们的数据是一样的，此时我们可以通过 inverse + compose 构建映射

    C++
    // gmem offset -> gA coord
inv_gA = left_inverse(gA)
// gC coord -> gA coord 
gC_to_gA = inv_gA.compose(gC) // gC -> gmem -> gA

    有了 gC -> gA 的映射过后，直接利用 compose gA -> rmem offset 的映射即可完成 gC -> rmem offset layout 的构建，因为 gC 和 rC 有相同的 shape，所以得到的就是 rC 的 layout

    C++
    // rA & gA has the same shape
// gC -> (gA = rA) -> rmem offset
rC = rA.compose(gC_to_gA)

mma tv layout solved by product & inverse

以上例子都需要有一个前提：不同的 partition 过后，thread 所获得的数据都是相同的。这个前提如何确保满足？我开始对 mma layout 进行了更多的研究，我发现 mma layout 只不过是同一种模式的复制粘贴：不断地重复一个 8x8 的 tile，其 tv layout 可写作

Python
# tv -> mn
mma_basic_layout = Layout(
    shape=[4, 8, 2],
    stride=[16, 1, 8]
)

image-20251104210802954

我们可以模仿 make_tiled_copy 中的方式，推导出这个 tv -> mn layout

C++
// (m1, n1) -> tid
auto mn2tid = make_layout(make_shape(_8{}, _4{}), make_stride(_4{}, _1{}));
// (m2, n2) -> vid
auto mn2vid = make_layout(make_shape(_1{}, _2{}), make_stride(_0{}, _1{}));

// ((m2, m1), (n2, n1)) -> (tid, vid)
// raked product to make v comes first
// ((_1,_8),(_2,_4)):((_0,_4),(_32,_1))
auto mn2tv = raked_product(mn2tid, mn2vid); 

// inverse & with shape
// (tid, vid) -> (m, n)
auto tv2mn = left_inverse(mn2tv).with_shape(make_shape(_32{}, _2{}));

其中 inverse 过后，如何确保 with_shape 一定是正确的？万一 inverse 过后的 shape 是 (vid, tid) 呢？不会，一定会是 (tid, vid)，这是由于 product & inverse 的性质所决定的：

  1. product 中，mn2vid 中的维度所对应的 stride 一定是被 multiply 的一方，这就决定了 vid 对应的 stride 会是最大的
  2. inverse 过后 stride 最大的 shape 会在最后（请回看 inverse 的推导过程）

两个性质决定了 inverse 过后一定会是 (tid, vid) 的排列顺序，所以我们用 with_shape 能够很方便进行 reshape

现在得到了 mma 中的 basic tv -> mn layout，那么上图中重复 4 次的 tv -> mn layout 如何得到？很简单，我们在其中使用一个 blocked product 重复 4 次即可

C++
// repeat (2, 2) mn -> tv
auto mn2tv_4x = blocked_product(mn2tv, make_layout(make_shape(_2{}, _2{})));
// inverse to get (t, v, 2, 2) -> (m, n)
// give all the repeat to v
// ((_4,_8),(_2,_2,_2)):((_32,_1),(_16,_8,_128))
auto tv2mn_2x = left_inverse(mn2tv_2x).with_shape(make_shape(_32{}, _8{}));

正如 product 和 inverse 的性质导致，重复的 mode 会在 inverse 之后的 shape 排在最后。我们有一个 (2, 2) 的 blocked product，不过我们到底是重复 4 次 t，还是重复 4 次 v，还是 tv 各自重复两次？这就需要根据需求进行 permute & reshape，在此情形下，是将 v 重复 4 次，所以直接用 with shape 即可，最后得到的 layout 和 mma traits 中的 layout 一模一样👏

除了上述重复方法外，还有一个方法，参考自 mma_atom.hpp 当中的 thrfrg_A：从扩张过后的 MN -> MN tensor 开始，利用 zipped divide 获得 tensor (AtomM, AtomN), (RestM, RestN)，然后利用 compose atom tv layouts 获得 (t, v), (RestM, RestN) layout，最后通过简单的 flatten & group 也可获得正确的 layout

with_shape 的实现本质是一个 compose，这也指导我们，reshape 可以使用 compose 直接完成，尤其是对某一个 mode 做 reshape 的时候可以用 compose(_, layout, ...) 来跳过其他 mode。注意当 layout.compose() 传入多个 layout 的时候会自动使用 make_tile(layouts) 进行 by mode compose。所以对于 nested layout 中的某一个 mode 进行 reshape 时，也应当使用 make_tile

然而对于 permute 没有优雅的方法，只有老老实实构建新的 tensor 了

  • _ 在 product, divide, compose 当中的作用

    在 compose 当中其实就是跳过某个 mode，另外没有 make_layout(_ ,)

    divide，只有 logical_divide(_, shape, ...) 是跳过某一个 mode，其他的 divide 都很难成功，zipped_divide 只有针对两个 shape 的时候才会成功

    product 无法使用 _ 进行跳过，不然 _ 会直接进入到 shape 当中，可以使用乘 1 的方式来跳过，最后使用 with shape 进行整合

Copy 连续性要求

我们通常不会考虑 copy 的连续性要求，因为由于 copy 与使用场景的强绑定性，连续性要求都是会被满足的，不过在此我仍然以 ldmatrix 为例子，看下该要求的基本形式。ldmatrix 其实是要求 src tv 中每一个 thread 所拥有的 8 个 values 在 shared memory 中是连续的。这种约束也存在在 universal copy 当中

C++
using R2SCopyAtomC = Copy_Atom<UniversalCopy<cute::uint16_t>, T>; // 16-bit contiguous
using R2SCopyAtomC = Copy_Atom<UniversalCopy<cute::uint32_t>, T>; // 32-bit contiguous
using R2SCopyAtomC = Copy_Atom<UniversalCopy<cute::uint64_t>, T>; // 64-bit contiguous

可以从 ldmatrix 中的 src tv 与 dst tv 之间的映射找到如下关系

Python
DST                     SRC      
----------------------------
T0~T3    V0~V1 <=> T0  V0~V7
T4~T7    V0~V1 <=> T1  V0~V7
...
T28~T31  V0~V1 <=> T7  V0~V7
----------------------------
T0~T3    V2~V3 <=> T8  V0~V7
T4~T7    V2~V3 <=> T9  V0~V7
...
T28~T31  V2~V3 <=> T15 V0~V7
----------------------------

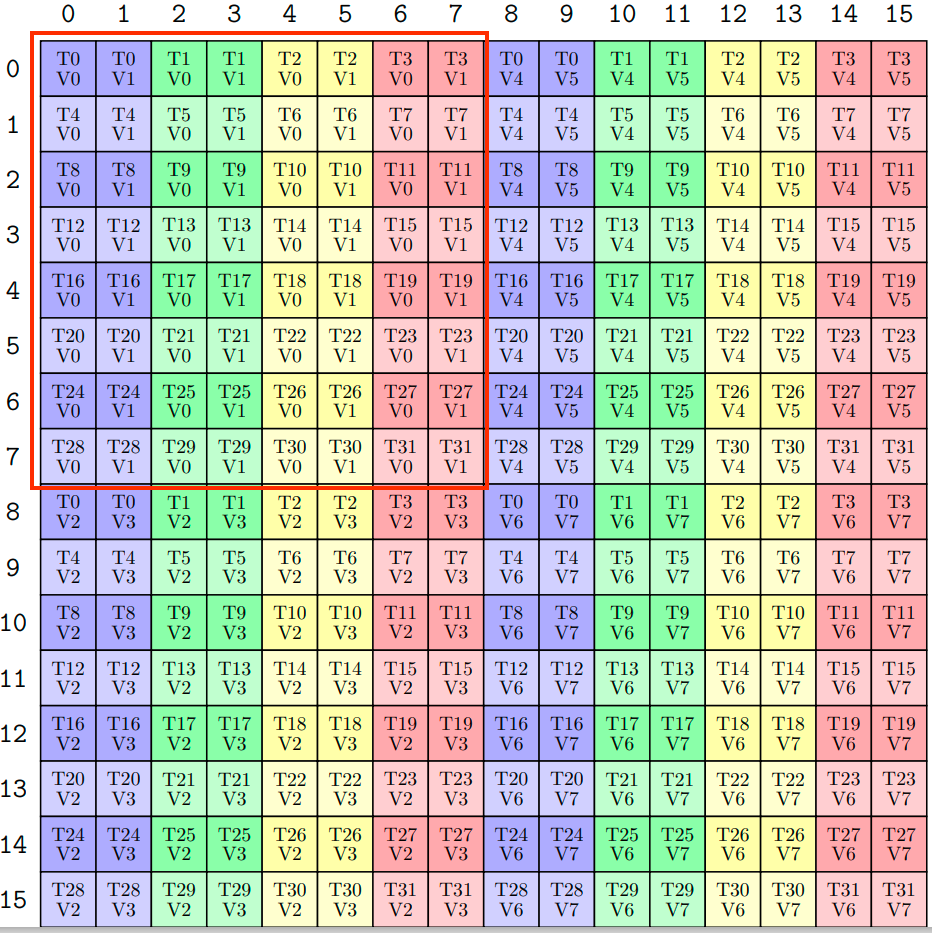
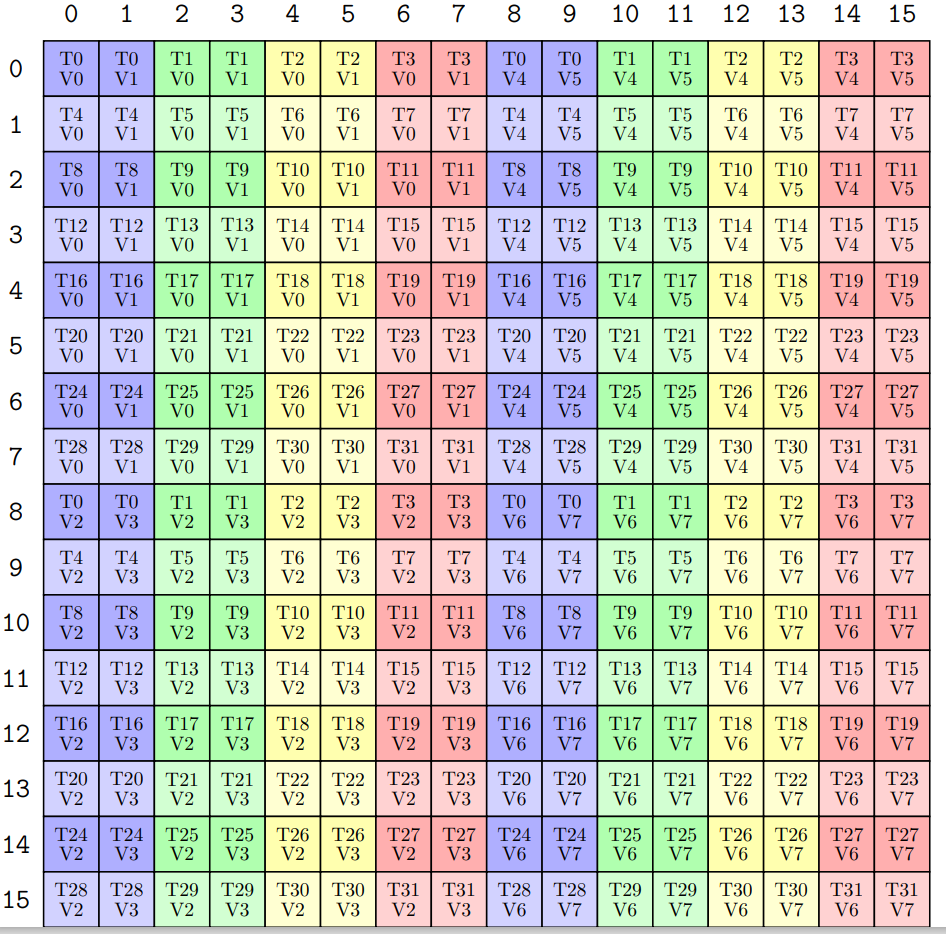
用语言描述一下第一行：dst T0~T3 线程的 V0~V1 数据，对应了 src T0 线程的 V0~V7 数据。对于 ldmatrix 而言，其要求 src thread 中的 V0~V7 在内存中是连续的。OK，现在我们就用 mma atom 的 tv layout 来实际看一下，其 src thread 中的 V0~V7 是否真的连续。以 SM80_16x8x16_F16F16F16F16_TN 中的 matrix A 的 (dst) tv layout 为例，用 print_latex 打出来得到如下排布

image-20250811163804449

我们可以发现 T0~T3 的 V0~V1 数据，正好是横向连续的 MK 坐标，这也说明了 T0 线程的 V0~V7 就是连续的 MK 坐标，但是为了保证内存的连续，MK -> Memory 的映射必须是 LayoutRight 即 row-major 排布内存，否则这些横向连续的 MK 坐标所对应的数据在内存仍然不连续

综上，在所给的 ldmatrix + mma layout + tensor layout 的条件下，copy 的连续性得到了满足。这也凸显出了三者的高度定制性：ldmatrix 必须和匹配的 mma layout 以及匹配的 tensor layout 进行使用，否则将会报错

Async Copy

在进行 copy 的时候经常会使用异步的 copy，即发出命令过后不会等待 copy 完成而是会继续执行后面的代码。但是我们也需要一些等待指令，以保证在计算时数据的确已经 copy 完成了。cutlass 提供了两个结构 cp_async_fence & cp_async_wait 用于完成这样的操作，在之后的 hgemm 实践中会有具体表现，这里先仅二者的功能

cp_async_fence

  • 这是一个内存屏障（fence）操作，用于标记当前所有已提交的异步拷贝（cp.async）任务的完成点。
  • 它的作用是确保在该 fence 之前的所有 cp.async 操作（即从全局内存到共享内存的异步拷贝）被视为一个批次，后续的 cp.async_wait 可以对这些批次进行同步。
  • 它并不阻塞线程，只是标记一个任务提交的边界。

cp_async_wait

  • 这是一个同步操作，用于等待之前提交的异步拷贝任务完成。
  • 参数 N 表示“等待除了最新的 N 个批次之外的所有批次完成”。例如：
    • cp_async_wait<0>：等待所有之前提交的异步拷贝完成。
    • cp_async_wait<1>：允许最多 1 个批次的异步拷贝未完成（即等待除最新提交的 1 个批次外的其他所有批次完成）。
  • 通常用于实现流水线的同步，确保数据在计算之前已经加载到共享内存。