CUTLASS CUTE 4 GEMM 核心优化与实践¶
约 6295 个字 111 行代码 8 张图片 预计阅读时间 33 分钟
核心优化¶
多级流水线 (Double Buffer)¶
多级流水线在 cute 之 GEMM流水线 中已经介绍地比较完善了,我这里将其中译中一下
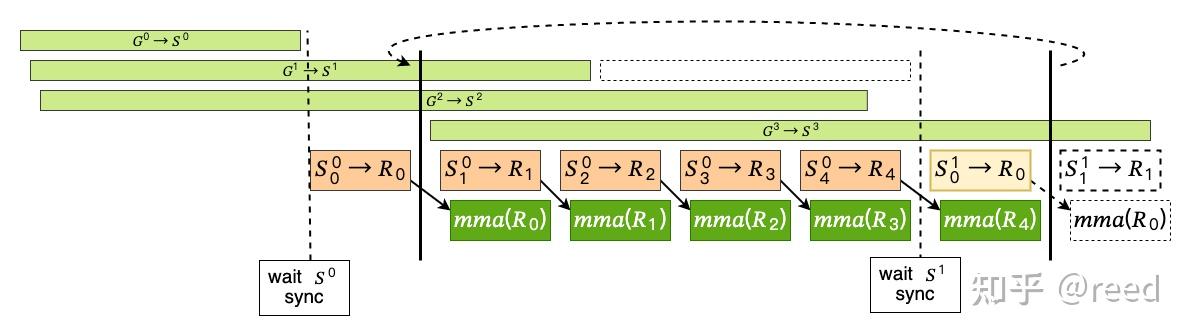
解释图中各个模块的含义:
-
浅绿色长方形代表:全局内存到共享内存的数据搬运\(G^i \rightarrow S^i\),上标\(i\)代表的是第\(i\)个 Tile 的数据(我称之为大 k 循环)
-
浅橙色长方形代表:共享内存到寄存器的数据搬运\(S_j \rightarrow R_j\),下标\(j\)代表的是第\(j\)个小 k 循环(Tile 内循环)
-
深绿色的长方形代表:TiledMMA 利用寄存器上的数据进行矩阵计算
-
黑色实线之间代表:完成一个 Tile 的矩阵运算(完整的小 k 循环)。并且黑色实线上方使用了曲线虚线进行了连接,代表完成了一个 Tile 计算之后继续计算下一个 Tile
-
黑色虚线代表:进行
cp_async_wait,等待 shared memory 搬运完毕
整个流水线的关键步骤:
-
首先将
Stage - 1个全局内存到共享内存的加载任务异步地发布出去(发布过后不进行等待,直接执行之后的任务) -
等待\(S^0\)的数据完成加载
-
在进入小 k 循环之前,首先从\(S^0\)中取出第一个小 k 循环所需要的数据,将其发送到寄存器上\(S_0\rightarrow R_0\)
-
此时正式进入到小 k 循环,可以分为 4 个要点:
- 发射异步读取新 Tile 的任务请求,即图中的\(G^3 \rightarrow S^3\)
- 从共享内存中异步读取下一个小 k 循环所需要的数据\(S_j\rightarrow R_j\)
- 执行第一个小 k 循环矩阵运算
- 重复步骤 2~3 直到当前小 k 循环完成
需要注意的是,在做最后一个小 k 循环时,我们需要读取下一个 Tile 中的第一个小 k 循环数据,该操作需要使用
cp_async_wait来保证下一 Tile 的数据已经完全加载到 shared memory 当中。这也是图中的虚线所表达的含义
我们也经常听说 double buffer 这个词,其实就是多级流水线的一个特例,即流水线的级数等于 2,级数数量就等于 buffer 数量。在上图所示的流水线中,shared memory 流水线级数为 4,register memory 流水线级数为 5
Swizzle¶
cute 之 Swizzle 已经将 swizzle 将得特别清楚了。这段话极其本质
回顾之前的介绍我们知道描述逻辑空间我们可以使用 Layout(本质是函数),而为了避免 bank 冲突,cute 中定义了 swizzle 抽象,swizzle 的本质也是函数,swizzle 作用在 layout 上,即函数作用在函数上,复合函数复合的定义。Layout 的作用是给定坐标返回 offset,而 swizzle 的作用则是给定 offset 返回 bank conflict free 的 offset。即
\[ offset_{\text{no-conflict}}=Swizzle(Layout(coord)) \]
通过 swizzle 获得了新的 layout,将 (M, N) -> offset 的位置进行改变。所以当在进行 read & write 时,会将数据读写到 swizzled position 从而避免 bank conflict
并且 swizzle (晃动/摇动) 这个名字特别的形象,想象你正在向 tensor x 的某个 coord (m, n) 写入数据
它本来该在 layout(coord) 位置写入该数据,结果 swizzle 了一下,写到了 swizzle(layout(coord)) 位置。物理位置对于读和写其实是无感的,因为读和写操作的是 tensor coord (m, n)
swizzle 不同于普通的 layout algebra,没办法用之前的 composition 来统一表达,但其本质仍然是函数映射。通过 M, B, S 三个参数来完全表示。最小单元为\(2^M\),而这个单元就是从 layout offset 顺序进行 group 和排序
swizzle 似乎给我上面的连续性分析带来了矛盾:swizzle 会打乱数据的连续性,但如果以\(2^M\)为单位的话,基本的连续性还是有保障的。例如\(2^3\)为单位的话,那么连续 8 个数据则都会是连续的,这就能满足 ldmatrix 的连续性要求
Swizzle 具体的计算过程在这里下不整理,在之后用 Swizzle 解决 bank conflict 处再详细说明,理解其意义,并且知道如何用 swizzle 来解决不同情况的 bank conflict
Bank Conflict¶
首先定义两个概念:
-
shared memory bank
共享内存被划分为多个独立的、等宽的存储单元,称为 Bank。每个 Bank 的宽度:4 bytes(32-bit)(所有现代 NVIDIA GPU 均如此)。Bank 总数:32 个(对应一个 Warp 的 32 个线程)
每个 Bank 可以独立读写,因此 32 个线程可以同时访问 32 个不同的 Bank(无冲突)。如果多个线程访问同一个 Bank 的不同地址,则发生 Bank Conflict,导致访问串行化
-
phase
1 个 Phase = 硬件一次性完成的 128B 数据传输(32 Banks × 4B)
线程参与 Phase 的方式:
每个线程的请求位宽 填满 128B 所需的线程数 是否典型优化 4B(32-bit) 32 线程 否(低效) 8B(64-bit) 16 线程 部分场景 16B(128-bit) 8 线程 是(最优) 为什么 8 线程 × 16B 是最优的?
- 减少指令数(1 条
LDG.128代替 4 条LDG.32) - 最大化带宽利用率(单次 Phase 完成更多数据搬运)
bank conflict 考虑范围的是一个 phase 内,不会考虑两个 phase 或更多,因为同时考虑两个 phase 一定会产生 bank conflict,因为一个 phase 就把 bank 宽度填满了,两个 phase 中必定有不同线程指向相同的 bank
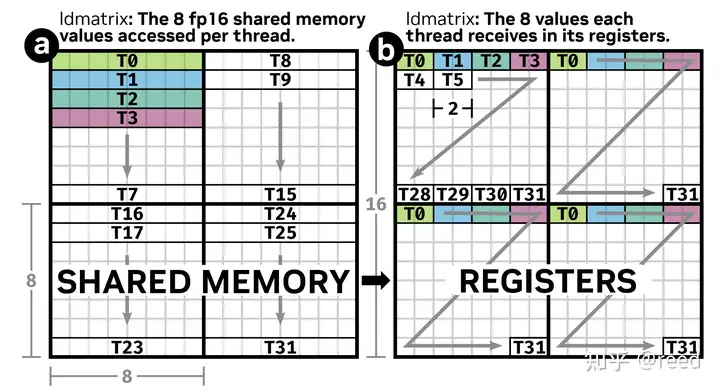
正如本文之前所示的 ldmatrix 示意图,一个黑色方框 (8x8 half matrix) 就是一次 phase 读取
update 2025/07/19 补充一下
LDG.128与合并访问之间的关系From Kimi
LDG128 是向量化加载指令,天然利于合并访存。在 CUDA 中,一个 warp(32线程)如果使用 LDG.128 连续访问内存地址,则:
- 每个线程请求 16 Byte;
- 整个 warp 请求 32 × 16 = 512 Byte;
- 如果地址对齐且连续,这 512 Byte 可以合并为 4 次 128 Byte 的事务(512/128 = 4)。
这极大提高了合并度(coalescing degree),减少 memory transaction 数量,提升带宽利用率。
使用4次
LDG.32仍然可能仅使用在 4 次 128 Byte 的内存事务完成,但是相比LDG.128会使用更多的指令,这也会消耗更多的时间。所以尽可能使用LDG.128指令 - 减少指令数(1 条
在 reed zhihu 中有一个分析 bank conflict 的思路
完整的512byte需要4个phase才能完成访问。这种情况也可以看作是:shared memory基本单元为16byte,总bank数为8,冲突与否的分析不在是32线程,而变成4个phase中的不同线程。如果采用64bit的访问形式,则相应的基本单元可以看作是8byte,总bank数目为16,冲突与否的条件变成两个phase内的线程是否冲突。整体上shared memory空间可以看作二维存储空间,其中列方向表示bank情况,行方向表示自由定义的大小。
我们可以从不同的粒度来构建简化过后的 shared memory 模型,方便我们分析。用这个模型来分析一个 16x16 or 16x64 size 的矩阵读写
所以Bank Conflict数量其实可以等价的理解为,在一个Phase内需要额外多少访存次数。From zhihu
理解 swizzle 以及其使用需要对多个概念进行熟悉。网络上的教程每一个都有自己对 swizzle 的定义和理解,我结合了三篇 blog 总结出自己对 swizzle 的理解:
- LeiMao-CuTe Swizzle,最为严谨的 blog,给出了准确概念,并且有实际例子与计算过程,能够推导出一般 swizzle 参数的计算公式
- Swizzle 本质思考,给出了逻辑行列和物理行列的思考模式
- 实用 Swizzle 教程系列,是第二篇 blog 的参考,我也列在这里
我将按照用五个部分来叙述 swizzle 概念以及其使用方法,并在最后给出解决 bank conflict 的一般思路
-
Swizzle Arguments,介绍 swizzle 概念
-
Introduce Examples,用例子来熟悉 swizzle 概念
-
Logical & Physical view,介绍逻辑 & 物理的不同视角来看到 swizzle bits
-
Common Examples,利用逻辑 & 物理 offset 分析一些常见例子
-
General Methods,给出一般解决思路
Swizzle in Bits¶
cutlass swizzle 其实是按地址的 bit 来解释的,其注释写得其实很清楚,但很容易被其迷惑的排版给迷惑了
// A generic Swizzle functor
/* 0bxxxxxxxxxxxxxxxYYYxxxxxxxZZZxxxx
* ^--^ MBase is the number of least-sig bits to keep constant
* ^-^ ^-^ BBits is the number of bits in the mask
* ^---------^ SShift is the distance to shift the YYY mask
* (pos shifts YYY to the right, neg shifts YYY to the left)
*
* e.g. Given
* 0bxxxxxxxxxxxxxxxYYYxxxxxxxZZZxxxx
* the result is
* 0bxxxxxxxxxxxxxxxYYYxxxxxxxAAAxxxx where AAA = ZZZ xor YYY
*/
swizzle 一共有3个参数:M, S, B。在 reed 的教程中分别解释为:基本单元包含的元素,一行包含的单位单元,有多少行。这当然是最直观的解释,不过现在我们要将这些参数用一般的 address 来看待。这里一个 address 是一个 32bit 的数据(可以数一下,上面注释一个地址包含了 32 个字母),下面是英译中
-
M or MBase,保持不变的位数量例子中用了 4bit,代表着一个基本单元包含 16 个元素。其中的字母都是一个 bit 其值为 0 or 1
-
B or BBits,mask 当中的位数量例子中用了 3bit,我们可以将其直观解释为“行号”
-
S or SShift,需要位移的位数量例子中用了 10 bit,我们可以将其直观解释为“列号”
例子中的直观解释:一个基本单元包含 16 个元素,一行包含了 1024 个基本单元,一共有 8 行。在进行 swizzle 计算时,其实就是用行号 YYY 和列号 ZZZ 进行了异或操作,获得了新的列号 AAA。这里有一个隐藏的限制:S <= B,否则无法有足够的位完成异或操作
异或操作由于其封闭性和双射性会将数据进行完美的重排,即不会有多个数据排到相同位置,也不会有数据排布到规定范围之外。下面用一些基本的例子来看如何利用 swizzle 将数据进行重排,从而避免 bank conflict
Introduce Examples¶
Example 1
读取一个 fp32 matrix 中的一列,matrix layout 为 Layout(shape=[32, 128], stride=[128, 1])
shared memory bank 一行能够装下 1024bit 的数据,矩阵的一行有 128 个 32bit 元素,会填满 4 行的 bank。假设我们读取第一列的数据,各个数据的 offset 根据 layout algebra 的运算为
由于 offset % 32 的结果都是 0,所以这些数据都会落在 bank0 的位置,会引起非常严重的 32-way bank conflict。读取其他列也是类似的情况
不过我们可以通过 swizzle 来解决这一个问题:
M = 0,一个基本单位包含 1 个 fp32 元素S = 7,一行包含 128 个基本单位B = 5,一共有 32 行
我们的 swizzle bit version表示如下
第一列的列号为 00000000,32行的行号为 00000~11111,通过异或操作对应的 5bit 得到新的列号(公式中加下划线的部分)
此时第一列的所有数据通过 swizzle 被分配到了 32 个不同的 bank,彻底解决了 bank conflict。其他列同理可证
Example 2
在 Example 1 的基础上,使用向量化内存读取(Vectoriezed Memory Access),让单个线程一次性读取或写入连续的多个数据元素。既然一个线程读取的数据变多了,那么一个 phase 所包含的线程数量就会减少。所以我们讨论的范围变为:用 8 个线程,每一个线程读取 4 个 fp32,即读取 matrix 当中的一个 (8, 4) 区域
如果未经过 swizzle,那么就会产生 8-way bank conflict,每一个线程的起始地址都在相同的 bank 当中
直接计算 swizzle 中的参数,就可以将这些在相同 bank 的地址,重排到其他地址当中\(\underline{xxx}\ yy\underline {yyy}\ zz\)
M = 2一个基本单位包含 4 个 fp32 元素S = 5一行包含 32=(128/4) 个基本单位B = 3一共有 8 行
另外再强调一个“显而易见”的事情:通常产生 bank conflict 的情况都是在访问“列”方向上,而不会出现在访问“行”方向上。因为一行中的数据本身就放在了不同的 bank 当中,并且我们讨论的范围还是一个 phase,即 32 个 bank 的总宽度,那么在访问连续的“行”数据时,一般是不会发生冲突的
在以上两个例子中你会发现他们的 M + B 都等于 5,他们的 M + S 都等于 7,这并不是巧合,而是我们推导 Swizzle 所遵循的公式
Logical & Physical view¶
这一节我将通过例子来介绍如何从逻辑视角转移到物理视角来解释如何计算 swizzle bits
Example 1
以一个 fp16 的 matrix 为例,其 matrix layout 为 Layout(shape=[16, 16], stride=[16, 1]),线程读取方式仍然是老图的左侧所示
我们先写一个其逻辑上的 swizzle bits
M = 3一个基本单位包含 8 个 fp16 元素,这里我们仍然假设是使用 128bit 向量化读取S = 1一行包含 2 个基本单位B = 4一共有 16 行
用 swizzle bits 的方式来看
但这样来看我们很难看出和 bank conflict 之间的关系。此时我们要以物理上的 swizzle bits 来看待。memory bank 一行有 1024bit 将包含 8 个基本元素,即 S = 3,再回到 Bank Conflict 小节的末尾,就能明白 reed 对于 bank 的一种逻辑抽象:此时我们可以认为一共有 8 个逻辑 bank
我们将这个 swizzle bits 修改为如下:B=2, S=3, M=3,相当于从 B 挪了两个 bit 到 S 当中
此时我们可以看到,\(xyy\)这 3bit 就对应了 bank 的一整行,即 8 个逻辑 bank。当\(xxy=000\)时就代表了逻辑 bank 0,此时对于前面两个 bit\(xx\)的任意值,他们都属于同一个逻辑 bank,所以会产生 bank conflict!再从逻辑视角来看,每 4 行会占据一整行的 bank 宽度,第 0,4,8,12 行的数据都会落在同一个 bank 当中
现在我们需要考虑线程读取的方式了,因为我们只考虑一个 phase 的读取,在本例当中,一个 phase 读取 (8, 8) 区域的矩阵,按照 swizzle bits 来算的话是 (8, 1) 个单位,即原来的\(xxxx\)4bit 表示 16 行,我们现在只考虑 8 行\(xxx\)
现在可以看到目前是第 0,4 行就会产生 2-way bank conflict,我们直接在这个位置上进行 xor 操作,把 bank conflict 解决
此时我们的 swizzle 表示为 Swizzle<B=1, S=3, M=3> 就可以把这些冲突给解开。不过如果我们并不是使用 ldmatrix 的读取方式,仍有可能读取不连续的 8 行,所以此时设置 Swizzle<B=2, S=3, M=3> 才能解决掉所有冲突
需要注意的是,ldmatrix 也可以使用 Swizzle<B=2, S=3, M=3> 来解决冲突,本质上该 swizzle 解决冲突的能力更强。按此推理,我们继续增加 B,使用 Swizzle<B=3, S=3, M=3> 也能够完全解决冲突。然而 B 的增加并不是没有上限的,其受限于逻辑 bank 的总数。在本例当中逻辑 bank 一共有 8 个,如果 B 超过 3 则没有足够的逻辑 bank 用于分配。B 也没有必要超过逻辑 bank 的总数,因为一个 phase 的大小就是逻辑 bank 的总大小,我们只需要考虑一个 phase 内可能产生冲突的情况
Example 2
在 Example 1 当中我们读取的是一个 (16, 16) 的矩阵,那么如果我们读取的是一个 (16, 32) 大小的矩阵,也是一个 phase 读取 (8, 8) 区域大小的数据,应该采用怎样的 swizzle 呢?
按照上面的分析我直接把这个 swizzle bits 写出
此时我们的 swizzle 表示为 Swizzle<B=2, S=3, M=3>,相比上一个例子多了一位的 mask bit,因为矩阵的一行会占一半的 bank,我们这样的读取方式会产生 4-way bank conflict,需要分配到 4 个不同的 bank 当中,所以 mask bit 需要为 2
同样的 Swizzle<B=3, S=3, M=3> 也能够解决上述冲突
General Methods¶
接下来我将给出 Swizzle 的通用公式,modified from LeiMao-CuTe Swizzle
Consitions:一个 phase 为 1024 bit,每个数据为 k bit,一行有 X 个,向量化读取一次读取 V 个元素
Target:读取不同的列时不产生 bank conflict
-
M是最好计算的参数,根据向量化读取的情况决定\[ M =\log_2{V} \] -
B按照解决冲突能力最强的 swizzle 来计算,即访问一个 phase 所有的 bank 都在同一个 logic bank 当中的情况\[ B=\log_2{\frac{1024}{k}} - M \]超过一个 phase 的情况则不在考虑范围内,因为不同 phase 之间不产生冲突
-
S的计算需要分情况讨论,这是因为 swizzle 要求S >= B-
一行数据
X未占满 bank:S和B相等\[ S=\log_2{\frac{1024}{k}} - M \]此情况没有被 LeiMao-CuTe Swizzle 所考虑,但是是必要的。其对应于上面例子中把\(x\)移动到\(y\)bit 部分,不会产生额外的 bank conflict,并满足
S >= B要求 -
一行数据
X已占满 bank:S将计算一行元素会包含多少基本单元\[ S=\log_2{X}-M \] -
所以两个公式合成一个公式
\[ S=\log_2{\max{(\frac{1024}{k},X)}} -M \]
-
该公式能够完美解决读取列数据产生 bank conflict 问题
不过还有一点我想要指出,以 fp16 的数据类型为例:如果一行数据很多,即 X 很多,那就需要大的 S,这意味着\(y\)bit 位数增加
访问的\(y\)bit 位置为 00xxx or 01xxx or 10xxx or 11xxx 时就会产生 bank conflict,他们都属于同一个逻辑 bank xxx。这是由于我们尝试一次读取不连续的行元素。如果我们总是读取连续的行元素,那么这种情况将不会发生,因为如果我们在读取连续的行元素时,如果出现了 bank conflict 的情况,说明这一行元素已经占满了完整的 bank 长度,也就是说会超过一个 phase 大小,从而避免 bank conflict
Epilogue¶
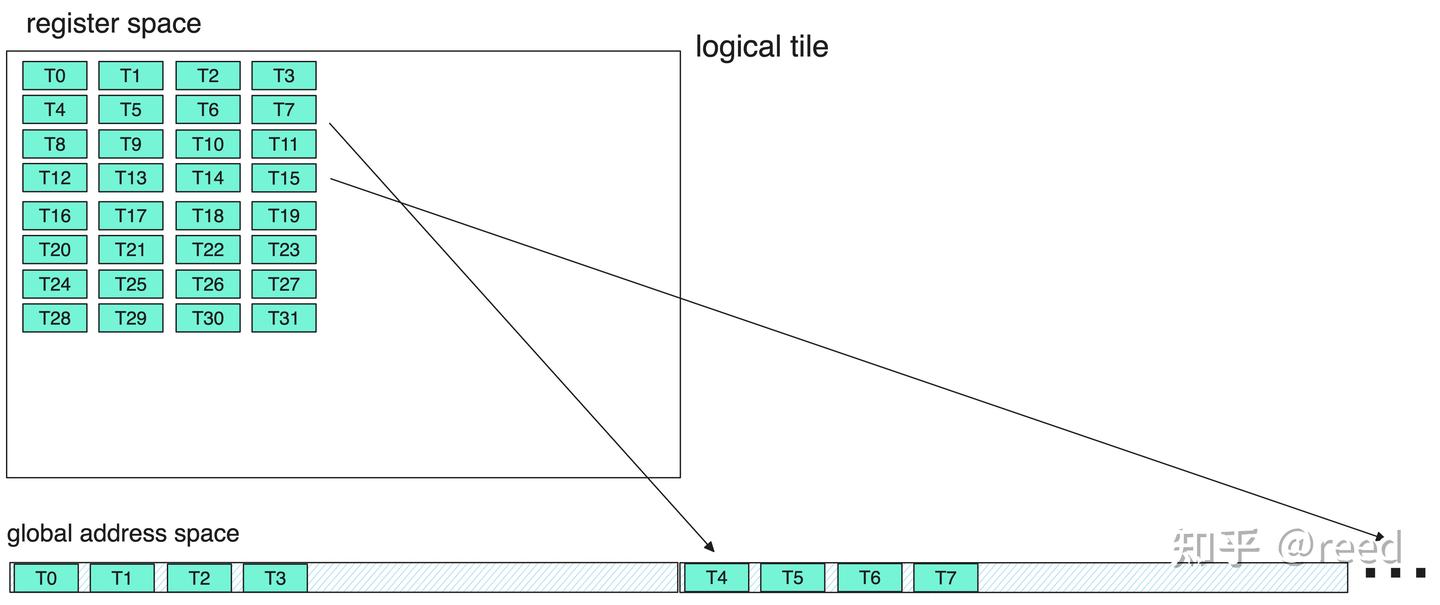
在计算完成后,我们需要将累加器(寄存器)中的结果,全部都运输到 global memory 当中存储起来。但直接完成这件事并不是最优选项,因为会造成不连续的数据写入(如下图),这样会导致存储时需要更多的内存事务,而不能使用向量化存储指令(STG.128)
针对这个问题,cute 中专门提供了 Epilogue 来通过共享内存作为中间媒介。先将寄存器数据存储到共享内存,然后再从共享内存中以更连续、更高位宽的形式存储到全局内存中去。对于 half 元素来说应该至少让一行有 8 个元素进行运输,这样就能用 128bit 的向量化存储指令了
hgemm 实践¶
我在之前的笔记中提出了一个:tile centric CUDA programming 的思路,在这一小节中我将沿着这个核心思路,并进行更详细地拓展,利用这些思想解决高性能 hgemm kernel。这些思路也是借鉴了 tilelang 的 demo
在此我提出一个 2-level tile 的概念:
- first-level: CTA Tile。作为最高 level 的 tile,该 level 非常方便我们设计宏观的 pipeline,e.g.: multi-stage or producer-consumer pipeline
- second-level tile 会有许多种,其核心是具体解决 CTA tile 的各阶段问题,包含:各个阶段的 cta tile copy;计算 cta tile mma
tilelang 将专注于 first-level tile programming,把 pipeline 和 second level tile 问题都自动解决了,这给我们设计 kernel 带来了极大的便利,这必定是以后的大趋势。不过在此我们仍然要讨论清楚这些细节
- 可以从不同的 level 来设计流水线:from cta tile level to second-tile level,pipeline inside of a pipeline
Define tile¶
我们以 tile 为 centric 作为构建模块,而 tile 的核心参考就是 mma shape。以 SM80_16x8x16_F16F16F16F16_TN 作为 mma op,其 mnk shape 为 (16, 8, 16),我们以此为基础推理出合理的 tile 设置。为了方便讨论,我们把条件设置更具体一些:使用 4 个 warps,以 (2, 2) 的 layout 进行排列
- mma mnk tile 的大小将从单个 warp 的形状
(16, 8, 16)扩展为 4 个 warp 的形状(32, 16, 16) - g2s tile,一定要使用向量化读写,每一个 thread 将对应 128-bit 数据(i.e. 8 个 fp16),128 个线程则能够复制 1024 个 fp16 数据,我们可以构建一个
(32, 32)的 tile - s2r tile,需要满足 mma 的特殊 tv 要求,同时满足 ldsm 命令的合法性(size of v 必须为 8),我们需要在 mma shape 的 N 维度上进行扩展,构建出
(32, 32, 16)的 tile,为什么要扩展两倍,请参考 TiledMMA & ldmatrix 小节 - r2s tile,可以使用
(32, 32)的 tile,注意由于 register 的特殊排布,无法使用 128-bit 的向量化读写 - s2g tile,可以使用
(32, 32)的 tile,使用高效的向量化读写
以上是 second-level tile 的设置,对于 cta mnk tile 的设置我们可以设置为 (128, 128, 32),其中有两个参考理由:
- 我们需要较大的 cta tile size 来增加计算时间,从而掩藏 copy 时间
- 需要使用 double buffer,所以扩大了 k 方向大小
Define smem¶
在 gemm 算法中定义 shared memory 主要从 3 个方面来考量:
- 定义一个 block 需要处理的 Tiler MN shape(区别于 tiled mma mn shape)
- 定义 shared memory 流水线 stages
- 定义 register 流水线 stages
在 hgemm 实践中我们定义为如下:
- 一个 block 需要处理
(128, 128)区域的 MN 矩阵乘法(Matrix C view) - shared memory 流水线为 3 级
- register 流水线为 2 级
根据以上定义我们可以计算得到所需要的 shared memory 大小以及 swizzle
- matrix A & B 各需要
(128, 32, 3)大小的 shared memory,其中32 = 16 * 2代表了 register 的两级流水线,会在小 k 循环中进行 2 次。最后一个维度3则代表了 shared memory 的 3 级流水线 - matrix C 并不需要全部存储到 shared memory 当中,shared memory 只是作为一个中转站以方便进行向量化读取,所以需要
(32, 32)大小即可,在 reed 所给代码中使用了(32, 32, 2)的大小,相当于申请了更大的 shared memory 作为中转,但在我的实验过程中发现加速效果不明显 - 根据之前的 swizzle 计算思路,我们只讨论一个 phase 当中的 shared memory 读取,也就是
(8, 32)大小的 shared memory 读取。那么利用公式可以得到Swizzle<B=2, S=3, M=3>,而在 reed 所给代码中则使用了Swizzle<B=3, S=3, M=3>其能够处理更大范围的 bank conflict
Pipelines¶
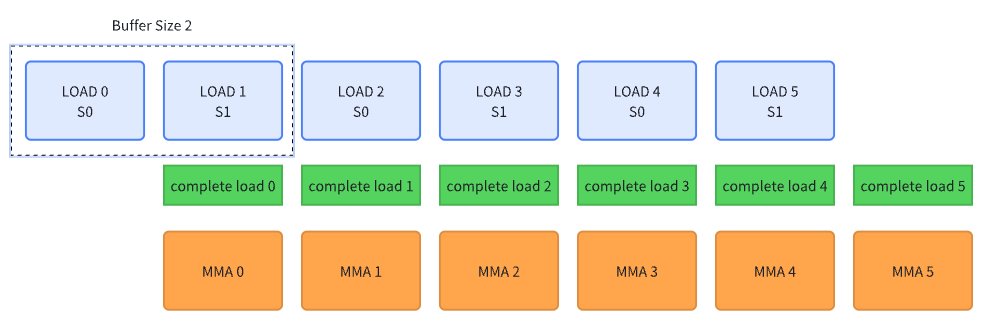
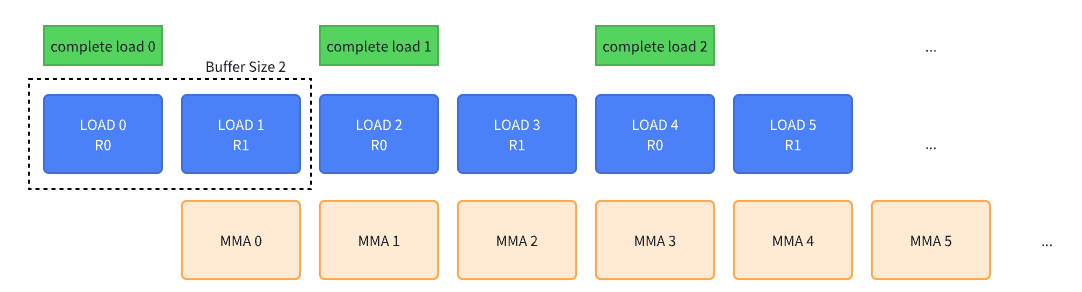
在之前我只是对 reed multi-stage pipeline 进行了简单的描述。可是要自己构建一个流水线应该如何做到?其实流水线的核心非常简单,就是任务重叠,具体到 GPU model 当中就是数据搬运与计算的重叠。最简单有效的 pipeline 就是 double buffer pipeline,可以用下图表示,横向为时间
在重叠二者的编程中,有2个关键的要素:
- 在计算当前 data MMA 时,同时预取下一个 data
- 在计算当前 data MMA 时,必须确保当前 data 填充完毕
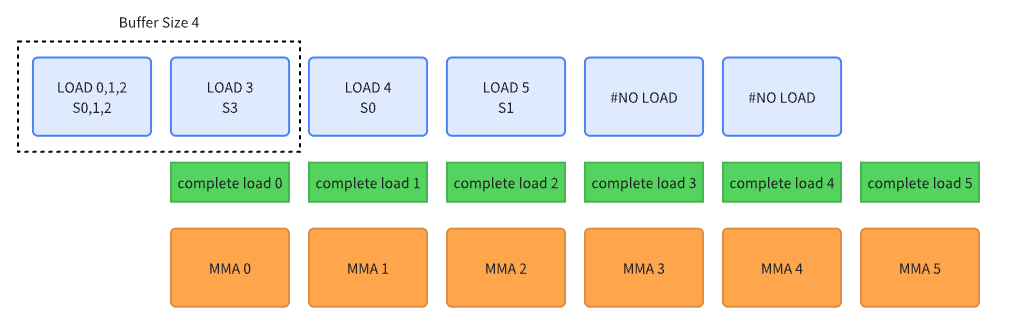
在具体实现时还有一些细节,例如计算 buffer index,以及在循环正式开始之前需要做的前置操作(e.g. 0-data load)等等。如果把 double buffer 进行扩展,有多个 buffer(也被称为 multi-stage),可以用下图表示
以上展示了一个 4 buffer 的流水线过程。我们先预先发起 3 个 buffer 的数据搬运,在真实计算 MMA 0 的时候发起最后一个 buffer 的数据预取,这能够让我们预取更多的数据。我认为这并不是典型的 producer-consumer model,因为 producer 并不是持续地在进行搬运数据,而是在当前 MMA 计算时,同时去预取了下一个 data
在上图中 MMA 直接从 shared memory 中获得数据开始计算了,实际上在 sm80 架构上 MMA 需要从 register 获得数据进行计算。所以有一个 smem -> register 的数据搬运过程。这个过程也可以用 double buffer 的思路进行流水线并行,所以两个流水线构成了 pipeline in the pipeline。两个 pipeline 会有数据上的依赖性,具体来说 register pipeline 中要求对应的 shared memory 必须完成 copy,这一点需要在编程中显示确认。下图展示了一个 double register buffer 的 pipeline 示意图,每两个 register 将消耗一批 smem buffer,每两个 MMA 计算完成一批数据
在实现过程中,我们可以逐层地实现 pipeline,把第 0 批的数据先预取好,然后直接开启 pipeline 循环。对于 epilogue 似乎没有使用 pipeline,可以直接按照常规的方案逐 tile 进行 regsiter -> smem -> gmem 搬运
Pseudo code¶
问题定义与上述相同:解决 MNK = (4096, 4096, 1024) 矩阵乘,CTA Tile 为 (128, 128, 32),CTA threads 为 128,warp layout (2, 2),smem 有 3 个 stages
// CTATile_MNK = (128, 128, 32)
// gA (CTATile_M, CTATile_K, num_k)
// gB (CTATile_N, CTATile_K, num_k)
// gC (CTATile_M, CTATile_N)
// sA (CTATile_M, CTATile_K, stages)
// sB (CTATile_N, CTATile_K, stages)
// tiled_mma (32, 16, 16)
// tiled_g2s (32, 32)
// tiled_s2r (32, 32, 16)
// tiled_r2s (32, 32)
// tiled_s2g (32, 32)
// register allocation
TiledMMA tiled_mma; // (32, 16, 16)
auto thr_mma = tiled_mma.get_slice(idx);
auto t_rA = thr_mma.partition_fragment_A(gA(_, _, 0)); // (8, 128/32, 32/16)
auto t_rB = thr_mma.partition_fragment_B(gB(_, _, 0)); // (4, 128/16, 32/16)
auto t_rC = thr_mma.partition_fragment_C(gC(_, _)); // (8, 128/32, 128/16)
clear(t_rC);
// g2s copy partition
G2STiledCopy tiled_g2s; // (32, 32)
auto thr_g2s = tiled_g2s.get_slice(idx);
auto t_g2s_gA = thr_g2s.partition_S(gA); // (8, 128/32, 32/32, num_k)
auto t_g2s_sA = thr_g2s.partition_D(sA); // (8, 4, 1, stages)
auto t_g2s_gB = thr_g2s.partition_S(gB); // (8, 4, 1, num_k)
auto t_g2s_sB = thr_g2s.partition_D(sB); // (8, 4, 1, stages)
// s2r copy partition
S2RTiledCopyA tiled_s2r_A; // (32, 16)
S2RTiledCopyB tiled_s2r_B; // (32, 16)
auto thr_s2r_A = tiled_s2r_A.get_slice(idx);
auto thr_s2r_B = tiled_s2r_B.get_slice(idx);
auto t_s2r_sA = thr_s2r_A.partition_S(sA); // (8, 4, 2, stages)
auto t_s2r_rA = thr_s2r_A.retile_D(t_rA); // (8, 4, 2)
auto t_s2r_sB = thr_s2r_B.partition_S(sB); // (8, 4, 2, stages)
auto t_s2r_rB = thr_s2r_B.retile_D(t_rB); // (8, 4, 2)
// prepare before mainloop
// 1. launch the stages - 1 copy
// 2. launch s2r first small iter k copy
constexpr int stages = Stages;
int load_tile_idx = 0;
int mma_tile_idx = 0;
for (int istage=0; istage < stages - 1; istage++){
copy(tiled_g2s, t_g2s_gA(_, _, _, istage), t_g2s_sA(_, _, _, istage));
copy(tiled_g2s, t_g2s_gB(_, _, _, istage), t_g2s_sB(_, _, _, istage));
cp_async_fence(); // commit
load_tile_idx++;
}
cp_async_wait<stages - 2>();
__syncthreads();
copy(tiled_s2r_A, t_s2r_sA(_, _, 0, 0), t_s2r_rA(_, _, 0));
copy(tiled_s2r_B, t_s2r_sB(_, _, 0, 0), t_s2r_rB(_, _, 0));
// mainloop
int num_k = size<3>(t_g2s_gA);
int num_k_inner = size<2>(t_s2r_rA);
int buffer_idx = 0;
for (int itile = 0; itile < num_k; itile++) {
// load next k tile
if (load_tile_idx < num_k) {
buffer_idx = load_tile_idx % stages;
copy(tiled_g2s, t_g2s_gA(_, _, _, load_tile_idx), t_g2s_sA(_, _, _, buffer_idx));
copy(tiled_g2s, t_g2s_gB(_, _, _, load_tile_idx), t_g2s_sB(_, _, _, buffer_idx));
load_tile_idx++;
}
cp_async_fence();
// small k iteration
for (int ik = 0; ik < num_k_inner; ik++) {
// load next small k tile
if (ik == num_k_inner - 1){
// make sure the next k tile complete
cp_async_wait<stages - 2>();
__syncthreads();
}
int ik_next = (ik + 1) % num_k_inner;
// calculate read tile
int read_stage = (ik == num_k_inner - 1) ? (itile + 1) % stages : itile % stages;
copy(tiled_s2r_A, t_s2r_sA(_, _, ik_next, read_stage), t_s2r_rA(_, _, ik_next));
copy(tiled_s2r_B, t_s2r_sB(_, _, ik_next, read_stage), t_s2r_rB(_, _, ik_next));
// gemm
gemm(tiled_mma, t_rC, t_rA(_, _, ik), t_rB(_, _, ik), t_rC);
}
}
可以看到大量代码其实不是在 mainloop 当中,而是在资源申请和数据切分,本身流水线还是非常清晰!
总结¶
如何学习一个陌生且没有那么多资料的领域?
一些描述对于我来说或许非常抽象:数学公式,C++...但实际上这些都是非常清晰的描述,如果转换成为 python 或者我熟悉的语言描述我就能很好地理解。而这个过程恰好是 GPT 比较擅长的:因为 GPT 对这些语言都非常熟悉,将一个语言翻译为另外一种语言基本上不在话下,只要所提供的描述是准确且基础的,通过切入到我所熟悉的语言,那么理解起来就事半功倍了。但是如果所问的问题是一个没有太多资料的复杂领域:例如 layout algebra,如果不提供基础的数学证明材料,很难获得一个让我满意的回答,我也无法完成对问题的解决
在学习 cutlass 的路上 Grok & DeepSeek 给与了很大的帮助,可以具体看下其解决了哪些疑问
-
Layout Algebra python scripts
利用原始数学证明材料写出了 layout algebra 各个基础运算的 python 代码。通过利用代码交互,能够更快地发现 layout algebra 中的一些性质
-
Compose first impression: fit spots to memory,但不够本质
对于 compose 的最终顿悟来源于对 right inverse 的理解,彻底理解了 compose 是“映射”,赋予映射的 source domain & target domain 以含义具有重要意义
-
Cutlass recasting
利用清晰的 C++ 代码得出了 recast 的算法过程
-
Swizzle Parameters
利用 Lei Mao's blog 的清晰描述与定义,给出了 swizzle 例子的中间推导过程,理解 swizzle in bits 形式
重大的突破其实来源于清晰的学习目标以及选择优秀的学习材料。我需要学习材料包含足够多的上下文以支持我去完成所指定的目标。上下文主要包含几点:1. 清晰的文档结构与教程;2. 足够简洁的原理代码;3. 准确的公式推导(与第一点有所重叠)
三点钟任意满足一点就是不错的材料,满足两点就是非常优秀的材料。因为有了 GPT 的存在,对于不熟悉的领域可以“翻译”成为你所熟悉的语言,方便你进行理解:例如 c++ -> python or math -> python,并且可以通过构建最小例子来完成特例到通用的抽象化理解。所以拥有了好的学习材料,很大程度上就能保证学习的成功