Denoising Diffusion Probabilistic Models¶

2025-12-152025-12-15

DDPM arxiv

Understanding Diffusion Models: A Unified Perspective arxiv

bilibili-扩散模型 - Diffusion Model【李宏毅2023】 PPT1 PPT2 PPT3 course page

本文档根据李宏毅视频整理得到，希望回答以下问题：

1. How to train and inference a diffusion model
2. What are the basic mathmatics behind it
3. How SOTA models improve the original diffusion model
4. What are the insights of diffusion can give us

Notaions in Probability¶

-\(x\sim p(·)\)代表着\(x\)是一个随机变量服从于概率分布\(p\)，在论文中，也常常用该 notation 来表示在\(p\)分布中采样\(x\)
-\(E_{x\sim p(x)}\)代表着求解变量\(x\)的期望，并且该变量服从概率分布\(p(x)\)，有时候也会用\(E_{p(x)}\)​ 来简写该过程
-\(N(x;\mu, \sigma^2)\)来表示一个高斯分布，其中随机变量为\(x\)，其均值和方差分别为\(\mu, \sigma^2\)，有时候也会省略掉\(x\)，直接写作\(N(\mu, \sigma^2)\)。对于一个多维高斯分布使用如下 notation:\(N(x;\mu,\Sigma)\)，其中\(x,\mu\)都是多维向量，而\(\Sigma\)为协方差矩阵 (covariance matrix)

Fundamental Maths¶

总结理解 VAE & Diffusion model 所需要的基础数学，主要就是贝叶斯理论（Bayesian Theorem）以及相关的概率论基础

Bayesian Theorem & Bayesian Inference¶

wiki Bayes' theorem (alternatively Bayes' law or Bayes' rule, after Thomas Bayes) gives a mathematical rule for inverting conditional probabilities, allowing one to find the probability of a cause given its effect.

上面就是 wiki 的第一句话，是对贝叶斯理论的高度总结：find the probability of a cause given its effect，给定这些现象来寻找原因。这个功能是一个非常强大的功能，但其公式却相当的简单

这里的 A 和 B 都是任意的随机事件，并且 P(B) 不为 0。这里的 A 和 B 看起来非常的抽象，如何对应到实际应用当中？在现实中，A 通常用来表示 Hypothesis，即我们的假设，B 通常用来表示 Evidence，即发生的现象，所以也通常看到下方的字母表示

为了更进一步理解，我们将这几个概率表示的意义写作如下：

1.\(P(H)\)，Prior，先验。我们通常称 hypothesis 为先验
2.\(P(E)\)，Evidence。名称没有变化
3.\(P(E|H)\)，Likelihood，似然。基于 hypothesis 所得出的事件概率即为似然
4.\(P(H|E)\)​，Posterior，后验。基于 evidence 所更新的 hypothesis

此时贝叶斯公式的功能变得更加具象起来：根据事实来更新我们的假设。那么这个假设到底是什么？事实又是什么？用一个更加具象的例子表示：

这下子符号似乎看起来更熟悉了：\(\theta\)就是模型参数，\(X\)就是数据样本，我们的任务就是用模型来估计样本的分布。其中我们用\(\theta\)来表示了我们的模型参数，其实这是一个 over simplification，其中还包含了我们的建模假设，例如：这个模型是一个高斯分布，且数据的分布符合高斯分布，高斯分布的参数为\(\theta\)。所以我们能够非常轻松地根据这个假设计算得到\(P(X|\theta)\)​，直接根据高斯分布来算就行了

理解这个公式最常举的例子就是抛硬币的例子：

我们将上述的变量都进行具体的定义

-\(\theta\)是一个随机变量，其决定了硬币为正面的概率
-\(X\)是实验结果，我们的实验结果为抛10次硬币，有7次为正面，3次为反面

首先我们需要有一个初始猜测：\(\theta\)到底是个什么分布？由于一开始我们没有任何信息，不如假设为最简单的 uniform distribution (均匀分布)\(P(\theta)=1, \theta\in [0,1]\)

我们可以很容易根据我们的假设计算得到我们的 likelihood

OK，现在比较难的是求得\(P(X)\)，这里需要使用全概率公式，不过好在我们也能够求到

最后求得\(P(X)≈0.1\)，是一个常数。所以将所有的结果导入到贝叶斯公式当中，就可以得到

可以看到，现在我们的\(\theta\)被更新为了一个 beta distribution，相比于之前的 uniform distribution 改动不小。如果实验量足够多，那么我们所算出的\(\theta\)应该趋近于一个 delta 分布，收敛到\(\frac{heads}{trials}\)​ 这个值，并且无论你的初始\(P(\theta)\)是多少，都会收敛到最终这个分布上。所以这给我一个启发：

无论初始\(P(\theta)\)分布是怎样的，所收获到的\(P(X|\theta)\)更新都是一样的，这是由我们的建模所决定的，即我们的模型假设：\(\theta\)决定了硬币为正面的概率。并且如果更新的 likelihood 足够强，那么将完全覆盖之前的先验，以 likelihood 为基准

另外再提一点：我们在计算\(P(X)\)的时候能使用这个全概率公式，仍然是在我们的模型假设之下的。可以看到我们的模型假设贯穿了所有的计算过程，一个错误的模型假设，即使计算再多的参数，也无法获得好的后验概率

这是一个非常非常简单的例子，简单到通常会直接算\(\frac{heads}{trials}\)作为硬币为正的概率。过于简单的例子将掩盖掉两个问题

1. \(P(X|\theta)\)is actually really hard to model
2. \(P(X)\)is actually really hard to calculate

我询问了 DeepSeek，希望其举一个例子来说明为什么这两个问题在实际应用中非常难解。DeepSeek 给出的例子是引入了隐变量，让问题变得更加复杂

假设我们有两种硬币，硬币1的正面概率为\(p_1\)，硬币2的正面概率为\(p_2\)，且每次抛硬币前会以概率\(\alpha\)选择硬币1，以\(1-\alpha\)选择硬币2。我们观察到 n 次抛掷的结果\(X={x_1,x_2,...,x_n}\)（例如10次中有7次正面），但不知道每次抛的是哪个硬币。我们的目标是推断参数\(θ=(p1,p2,α)\)

此时我们需要获得\(P(X|\theta)\)​ 就不是那么容易的事儿了！可用公式表达为

式子中的各个概率计算如下：

可以看到，我们需要将所有可能的隐变量组合积分掉，才能获得最终的\(P(X|\theta)\)，这个计算复杂度是随着实验次数 n 而指数上升的，按照我们的条件则需要计算\(2^{10}\)项 。那么如果我们还要对这个式子进行全概率公式的积分，计算复杂度就更大了

即使采用数值积分，对于高维空间的积分成本也是非常高的，例如用网格法则需要\(O(k^3)\)

最后自己再高度总结一下导致这两个困难的原因：

1. 当模型包含隐变量时，似然的计算涉及高维求和或积分，导致计算量指数爆炸

2. 当参数空间维度增加或模型复杂时，\(P(X)\)的解析解不可得。高维会显著增加计算复杂度，而即使是低维有的式子的解析解仍然不可解，例如你无法对高斯分布求解定积分

   \[ P(X) = \int_{0}^{b} \int_{-a}^{a} \left[ \prod_{i=1}^n \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(z_i-\mu)^2}{2\sigma^2}} \right] d\sigma^2 d\mu. \]

为了解决上述问题，就需要近似方法了😏其中就包含变分推断和 MCMC 方法，而变分推断就是 VAE 的理论基础。而以上去寻找参数\(\theta\)的方法就被称作贝叶斯推理（Bayesian Inference）

FROM DeepSeek:

Bayesian Inference 是一种统计推断方法，基于贝叶斯定理。贝叶斯定理描述了在给定数据的情况下，如何更新我们对某个假设或参数的信念。具体来说，贝叶斯推断通过结合先验知识（prior）和新的观测数据（likelihood）来计算后验分布（posterior）

Joint & Conditional & Marginalize Distribution¶

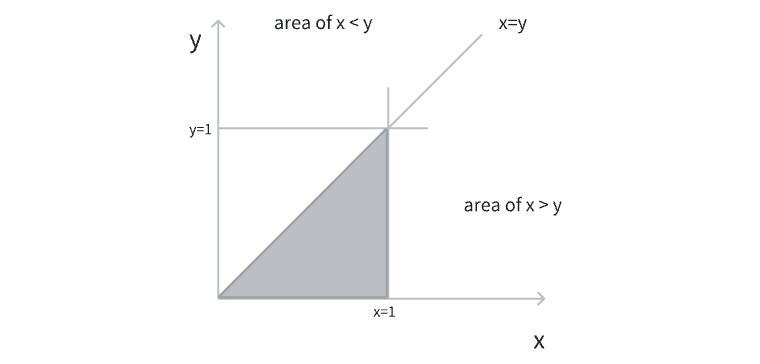
之前对这三个概念：联合分布、条件分布、边缘分布的概念非常模糊，我将以一个概率密度函数作为例子（询问 DeepSeek），并辅之以图像来帮助我深入理解这三者的概念与关系。从一个简单的联合概率密度分布出发

可以验证这个联合概率密度的积分为1，所以是合法的概率密度分布。用图像可表示如下

仅在有阴影的区域为概率密度不为零的区域。接下来可以直接求得各个条件分布和边缘分布，这里以\(p(x)\)和\(p(y|x)\)为例子

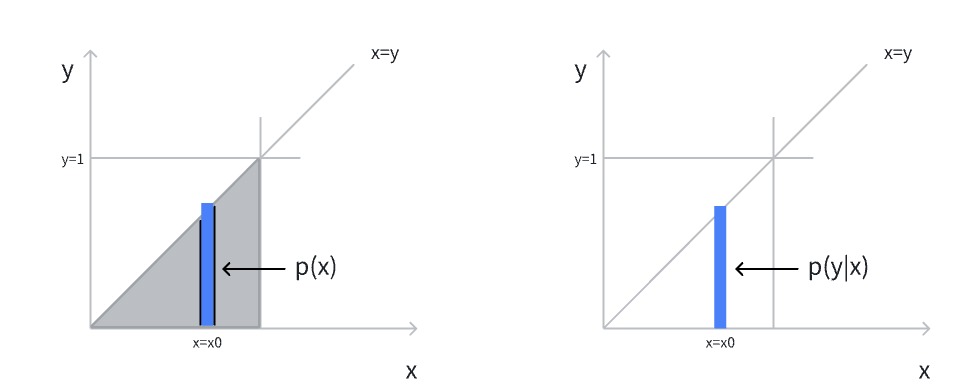
先直接从公式的角度来看下二者的特征，再从图像直观理解，最后作出总结。可以看到\(p(x)\)是随着\(x\)的增加而逐渐增加的（在有效范围内），而\(p(y|x)\)是随着\(x\)的增加而逐渐减少，甚至还有可能接近于无穷大！这两个公式所表现出的情况非常不一样，也和最初的简洁的联合分布天差地别。但是这一切都是合理的，可从下面的图像来直观理解（忽略冒出来的一点点小三角😂）

• 边缘分布

\(p(x)\)​ 将\(y\)​ 的影响直接通过积分去除掉，可以想象将\(y\)​ 方向的概率密度全部压缩到了\(x\)​ 轴上，这也许就是边缘的感觉，把高维的概率密度通过积分压缩到了低维的边缘。我在图中用一个蓝色区域来表示\(p(x=x_0)\)​ 时的概率密度，可以看到：随着\(x\)​ 的增加，蓝色区域的面积也将增加

• 条件分布

\(p(y|x)\)就需要把视角从全局放到局部上了。所以我把灰色的区域直接去除，仅留下了蓝色区域，此时这片蓝色区域就是我们全部的样本空间。此时\(y\)在这片区域的分布仍然是均匀的，其概率密度为\(\frac{1}{x}\)。随着\(x\)的减少，蓝色区域的面积也将减少，也就是样本空间的大小也越来越小，\(p(y)\)​ 的概率密度也越来越集中，最终趋近于无穷

通过上述过程对三者的关系有了直观的理解，现在总结一下他们的关系：联合分布为一个全局的分布，包含两个变量的完整分布；边缘分布降维过后的全局分布，将某个变量的概率密度压缩到低维边缘；条件分布为一个局部的分布，描述在某个子样本空间下，随机变量的分布

Chain of rules in probability¶

对于多个随机变量\(X_1,X_1,…,X_n\)，其联合分布可以通过链式法则逐步分解为条件概率的乘积：

每一步的条件概率都基于之前所有变量的信息

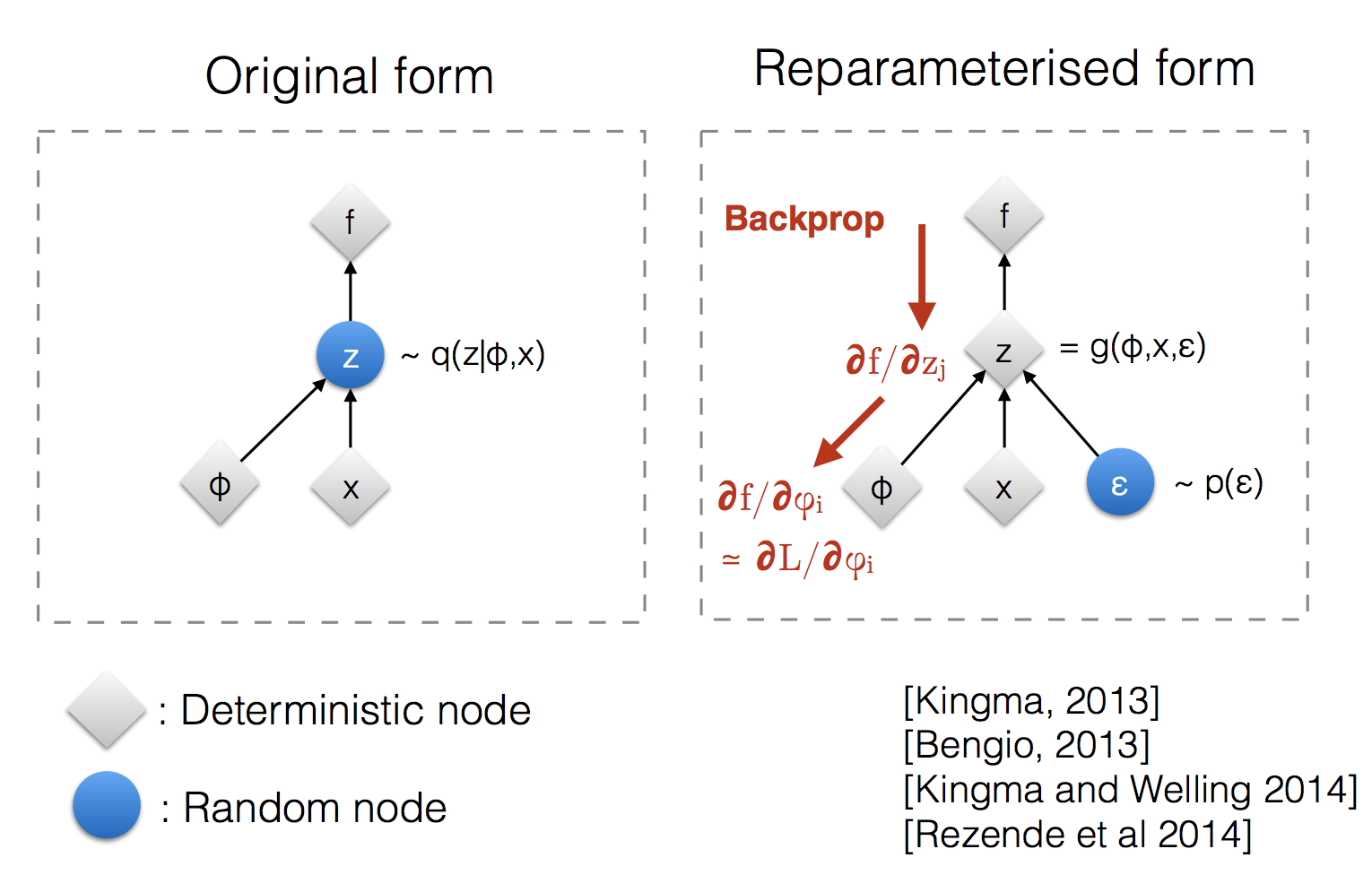
Reparameterization trick¶

wiki Lilian's blog

利用重参数化技巧，将变量的随机性转移到新构造的参数中，使得梯度能够顺利返回。在下图中原始随机变量为\(z\)，在进行反向传播算法时，由于随机性梯度无法回传。为了让梯度回传，引入新的随机变量\(\epsilon\)，由该变量承担随机噪声的作用

Importance Sampling¶

该方法用于 target distribution\(p*\)不太好采样时使用 proposal distribution\(q\)来获得采样结果。此时计算期望时需要乘以 ratio 来获得正确的期望

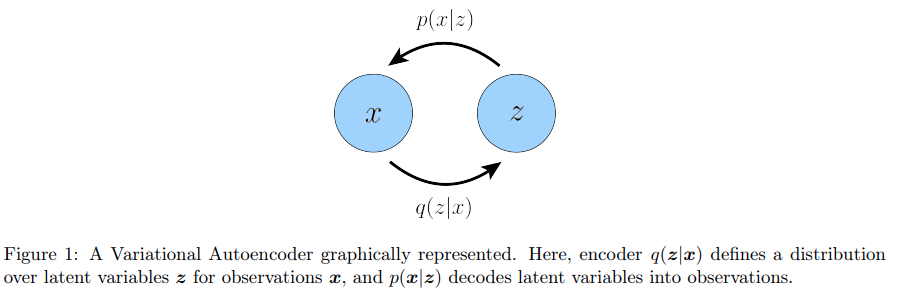
Inference & Generate¶

这是在看白板推导时看到的概念：推理和生成。过程\(p(x|z)\)是一个 generate 过程，即从隐变量生成观测变量，而\(q(z|x)\)是一个推理过程，即从观测变量生成隐变量

这里和之前所接触到的两个概念很像：判别式模型和生成式模型（discriminative & generative model），通常判别式模型的学习更加简单，只需要学习推理过程即可。而生成式模型则更加困难，我认为生成式模型通常要把推理和生成两个过程都学习了，也有人说生成式模型要学习的是联合分布\(p(x,z)\)

An intuitive perspective of DDPM¶

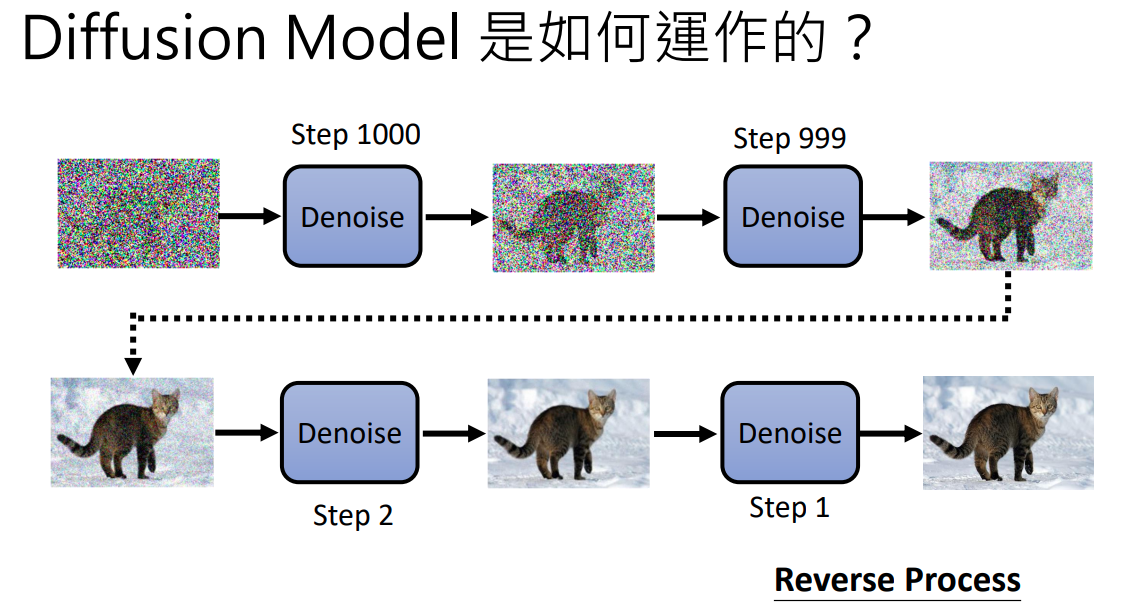
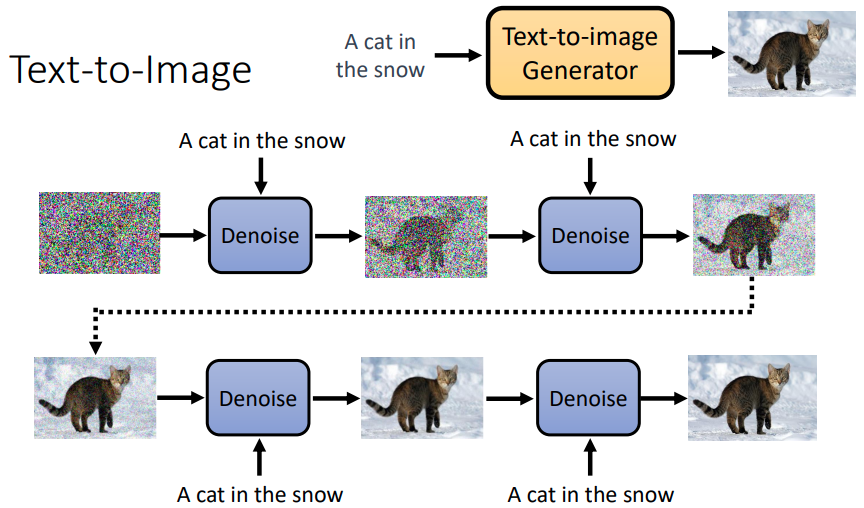
看图说话：DDPM 其实就是一个从随机噪声开始，不断去噪直到生成目标对象的过程。那到底会生成什么样的图像呢？根据上面的示意图，我们其实并没有给去噪模型任何的信息，只给了一个初始噪声就开始让其进行去噪，所以理论上会生成任意的图像。而现在 diffusion model 在 text-to-image 领域应用非常多，所以如果想要生成指定的图像，我们需要给 diffusion model 加入额外的信息，例如文字：

How to inference DDPM¶

• Algorithm

  

  Notation of the algorithm

  -\(\alpha_t, \bar{\alpha_t}\)​

  二者都是超参数，由我们自己决定。实际上这产生于另一个序列\(\beta_1,\beta_2,...\beta_t\)，这个序列代表了我们每一个 step 中噪声所占的比例，是一个递增的序列，并且属于 0~1 之间。简单来说，随着 forward step 的加深，我们向原图中加的噪声会越来越大，即噪声所占的比例会越来越大

  \[ \alpha_t = 1-\beta_t\\ \bar{\alpha_t}=\alpha_1\alpha_2...\alpha_t \]

  -\(\epsilon_\theta\)​

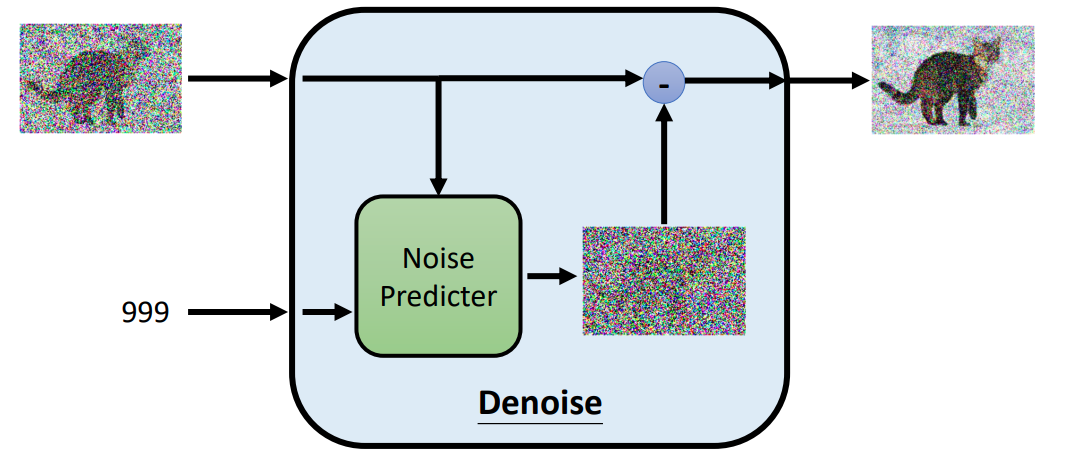
  其实就是 neural network，其参数用\(\theta\)表示，输入为\((x_t,t)\)，该网络的作用就是根据输入图像和 time step t，预测出加入到该图像的噪声\(\epsilon\)，然后用输入图像减去该噪声就能够获得去噪图像

  -\(\sigma_t\)

  仍然也是一个超参数，代表每一个 timestep t 额外加入的 variance

• Algorithm 示意图 (at time step 999)

  

How to train DDPM¶

• Algorithm

  

  DDPM 的训练算法也非常的简洁，简单来看就是用网络\(\epsilon_\theta\)去预测加入到样本中的噪声，希望这个预测噪声和真实加入的噪声足够的接近。但其实这个训练过程暗藏玄🐔，里面这些系数到底是什么意思呢？为什么在推理的时候似乎是一步一步地去噪，而这个过程在训练里没有呢？这些都需要在之后的数学推导中回答！

SOTA diffusion framework¶

• Overall Framework

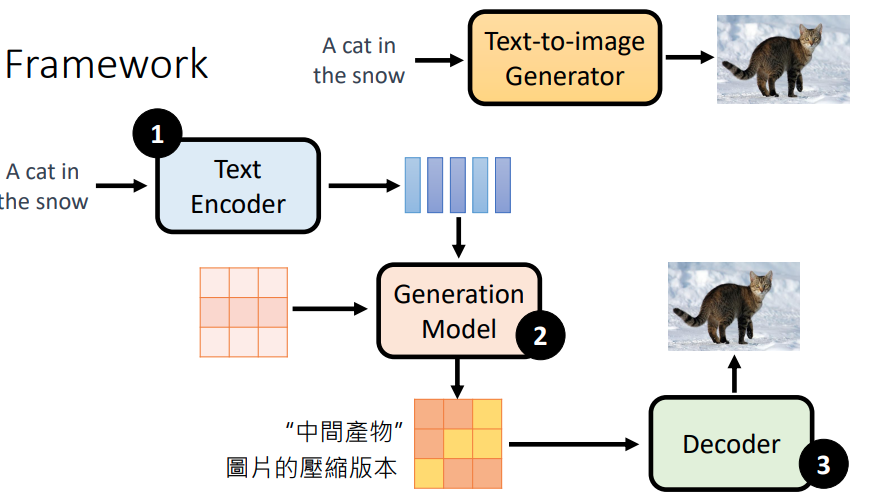
  现今 SOTA 的 text-to-image 模型都可以分为3大步骤：

  1. 使用 text encoder 将文字进行 encode，生成 text feature
  2. 使用 generation model 对噪声进行去噪。此时需要将 text feature 作为输入，经过模型后输出一个中间产物，该产物可以是 feature map，或者压缩的图片
  3. 对中间产物进行 decode，生成最终的图像

  

  这三个组件：text encoder, generation model, decoder 通常都是分开训练的。但是 generation model 是依赖于 decoder 的，因为 decoder 必须要认识 generation model 所产生的特征图。这实际上在训练 decoder 时，我们还训练了一个 auto encoder 来产生这个 latent representations (feature map)，然后通过向 latent representation 加入 noise 训练 generation model

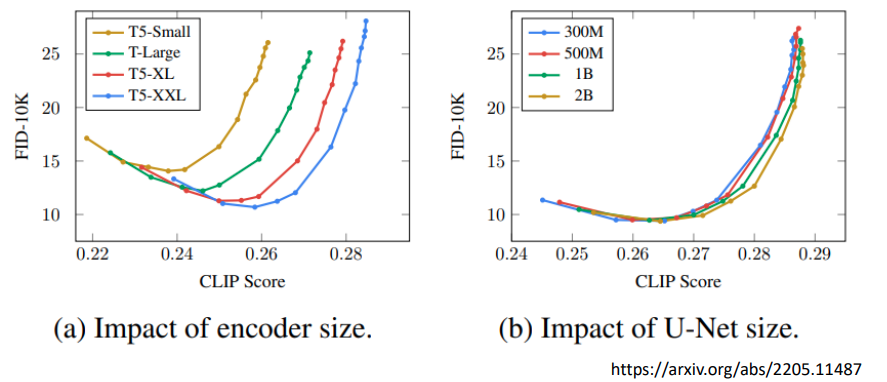
• Text encoder size 对于图像生成质量非常重要，而 vision encoder size 影响较小

  

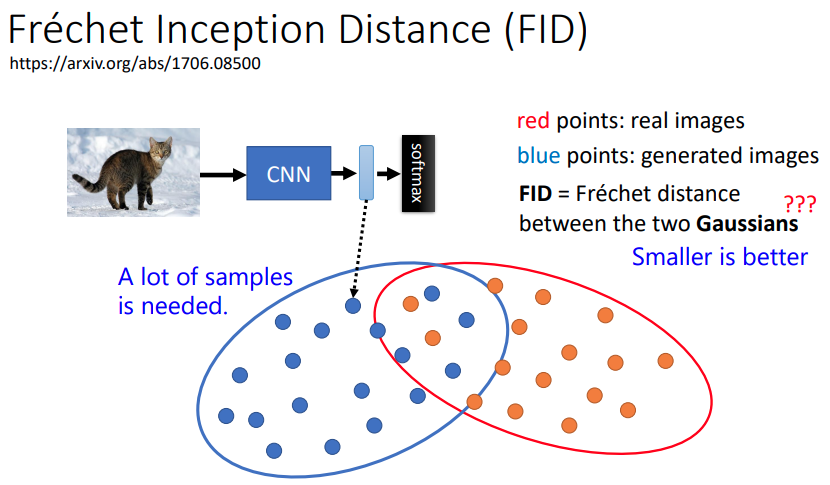
  FID Frechet Inception Distance 就是用来评价所生成的图像集与目标图像集之间的距离，FID 应该越小越好。可以看到随着 T5 模型的增加，FID 曲线是向着右下角移动，说明生成图像有显著改善

  

• 课程还介绍了 Stable Diffusion & DALL-E，我就不整理了

From ELBO to VAE¶

ELBO wiki 我能够从 EM algorithm 比较顺利地切入到 VAE 当中

Pre-request: why latent variable?¶

我们为什么要提出隐变量的概念？这个问题的回答是从文章 Understanding Diffusion Models: A Unified Perspective 中得到启发?

For many modalities, we can think of the data we observe as represented or generated by an associated unseen latent variable, which we can denote by random variable z. The best intuition for expressing this idea is through Plato’s Allegory of the Cave. In the allegory, a group of people are chained inside a cave their entire life and can only see the two-dimensional shadows projected onto a wall in front of them, which are generated by unseen three-dimensional objects passed before a fire. To such people, everything they observe is actually determined by higher-dimensional abstract concepts that they can never behold.

Analogously, the objects that we encounter in the actual world may also be generated as a function of some higher-level representations; for example, such representations may encapsulate abstract properties such as color, size, shape, and more. Whereas the cave people can never see (or even fully comprehend) the hidden objects, they can still reason and draw inferences about them; in a similar way, we can approximate latent representations that describe the data we observe

加粗的这句话就是对隐变量直觉的总结：我们几乎永远无法获得事件发生的真实根因，所以我们需要自己去估计/寻找/计算这些根因，用这些根因来描述所发生的现象。事实上，这似乎就是人类实验科学发展的途径：通过所观察的事实总结或验证规律。这些规律就是我们所寻找的隐变量

Variational Bayesian inference¶

在之前我简单总结了什么是 Bayesian Inference，现在需要了解一下什么是变分 variational

FROM DeepSeek:

Variational Methods 是一类用于近似复杂数学问题的技术，特别是在概率和统计中。变分方法的核心思想是通过优化来找到一个简单的近似分布，使其尽可能接近真实的后验分布。在变分贝叶斯推断中，我们选择一个参数化的分布族，并通过最小化某种损失函数（如KL散度）来找到最佳近似。这种方法在处理复杂模型或高维数据时特别有用，因为它可以避免直接计算难以处理的后验分布。

所以说变分其实就是一种思想：使用优化的方式来获得最优参数。我一直觉得 variational 这个词比较抽象，询问 DeepSeek 过后才发现这个词非常具象

From DeepSeek:

The term "variational" in variational Bayesian inference comes from calculus of variations, a branch of mathematics that deals with optimizing functionals (functions of functions).

• In calculus of variations, we study how small variations (tiny adjustments) to a function affect a quantity (e.g., minimizing energy or maximizing entropy).
• It mimics the calculus of variations: instead of varying a function (e.g., a curve), we vary the parameters of\(q(\theta)\)to optimize the approximation.

也就是说 variational 变的就是参数\(\theta\)。另外个人理解：\(\theta\)通过微小的变化所引起的损失函数的变化就能够引出梯度的计算，也就能使用反向传播算法来优化参数

下面将正式对 Variational Bayesian Inference 作出数学定义

Suppose we have an observable random variable\(X\), and we want to find its true distribution\(p\). This would allow us to generate data by sampling, and estimate probabilities of future events. In general, it is impossible to find\(p^*\)​ exactly, forcing us to search for a good approximation.

That is, we define a sufficiently large parametric family\(\{p_\theta\}_{\theta \in \Theta}\)of distributions, then solve for\(\min_{\theta} L(p_\theta, p^*)\)for some loss function\(L\). One possible way to solve this is by considering small variation from\(p_\theta\)to\(p_{\theta + \delta \theta}\), and solve for\(L(p_\theta, p^*) - L(p_{\theta + \delta \theta}, p^*) = 0\). This is a problem in the calculus of variations, thus it is called the variational method.

问题建模 1.0

• 定义隐变量\(Z\)，其分布\(p(z)\)为非常简单的分布（uniform or normal distribution）
• 定义函数\(f_\theta\)，通常为一个神经网络，其参数为\(\theta\)，输入为隐变量\(z\)。其作用是近似计算给定隐变量生成观测数据的过程
• 定义函数输出\(f_\theta(z)\)为新的概率分布的参数。例如我们可以定义\(f_\theta(z)=(f_1(z),f_2(z))\)为 normal distribution 的参数，前者为均值，后者为方差

如此建模能够很容易地通过采样来获得联合分布\(p_\theta(x,z)\)

This defines a family of joint distributions\(p_\theta\)over\((X, Z)\). It is very easy to sample\((x, z) \sim p_\theta\): simply sample\(z \sim p\), then compute\(f_\theta(z)\), and finally sample\(x \sim p_\theta(\cdot|z)\)using\(f_\theta(z)\)​.

接着我们需要计算\(p_\theta(x)\)，因为我们通常使用极大似然估计的方法来获得最优参数。在之前的 Fundamental Maths 章节中介绍了，可以使用全概率公式来进行计算

但是如之前所分析，由于高维度隐变量以及复杂神经网络建模，这个积分是没办法计算的😕此时需要另寻他路，好消息是通过贝叶斯法则我们还有一个求解方法

但是新的问题又出现了：如何获得\(p_\theta(z|x)\)🤔此时又只能求助于近似的力量，就像之前定义了一个神经网络来获得近似的\(p_\theta(x|z)\)分布，现在我们需要再定义一个新的参数组，来近似，即：\(q_\phi(z|x) ≈p_\theta(z|x)\)​。增加建模条件

问题建模 2.0

• 定义函数\(q_\phi\)，通常为一个神经网络，其参数为\(\phi\)，输入为观测数据\(x\)​。其作用是近似计算给定观测数据生成隐变量的过程

问题建模 3.0

这样随意的近似是合理的吗？我们其实并没有证明上述近似的合理性，但是随着深入分析目标函数，就能理解近似的合理性。现在我们引入需要优化的目标函数：expectation of log-likelihood

等式右侧的第一项就是真实分布的熵（entropy），第二项即为真实分布与近似分布的 KL 散度。可以看到第一项的熵是一个不包含参数\(\theta\)的项（可认为是常数），所以当我们在最大化期望时，等价于在最小化 KL 散度。进而推出：如果左侧期望为最大值，那么右侧的 KL 散度应该为0（可以用反证法轻松证明），此时\(p*=p_\theta\)，也就证明了使用用\(\theta\)近似的合理性。那么重点就是优化左侧的期望熵，不过我们要调整一下求得期望的形式，因为上述公式中的\(p*\)是不可知的。此时直接使用 importance sampling 的方法近似获得期望

注意：这里我们认为是 proposal distribution 和 target distribution 就是一样的，即：样本就是从\(p*\)分布中产生，所以不需要乘以 ratio 调整

Evidence Lower Bound (ELBO)¶

在上述过程中，我们建模了一个神经网络\(q_\phi\)来近似后验分布\(p_\theta(z|x)\)，但实际上我们不能够直接使用这个估计网络带入到目标函数当中，因为

如果我们去最大化等式的右侧，并不会带来等式左侧的值的上升，即：此优化算法的收敛性是没有保证的❌此时我们选择优化的是 Evidence lower bound (ELBO)

我这里直接列出等式

其中\(q_\phi(·|x)\)是任意的分布，ELBO 为等式右侧的第一项

等式推导过程如下，参考自 link

其实推导出 ELBO 的方法有很多，都离不开两个步骤：

1. 引进隐变量，并使用贝叶斯公式将其进行转换

   \[ p(x)=\frac{p(x,z)}{p(z|x)} \]

2. 对等式的两侧乘以\(q_\phi\)(not\(p_\theta\)) 进行积分以获得关于\(z\sim q_\phi\)的期望。这一步的积分看起来匪夷所思，如果从 KL 散度出发进行推导，这个积分才会比较自然地诞生，zhihu Lilian's blog

   \[ \text{KL}(q_\phi(z|x) \| p_\theta(z|x)) = \int_z q_\phi(z|x) \log \frac{q_\phi(z|x)}{p_\theta(z|x)} dz \]

   在上述博客中还介绍了 ELBO 的另一种常见形式，我也列在下面

   \[ \begin{aligned} ELBO &=\mathbb{E}_{q_{\boldsymbol{\phi}}(\boldsymbol{z}|\boldsymbol{x})} \left[ \log \frac{p_\theta(\boldsymbol{x}, \boldsymbol{z})}{q_{\boldsymbol{\phi}}(\boldsymbol{z}|\boldsymbol{x})} \right] \\ &= \log p_\theta(\boldsymbol{x|z}) - KL(q_{\boldsymbol{\phi}}(\boldsymbol{z}|\boldsymbol{x}) \parallel p_\theta(\boldsymbol{z})) \end {aligned} \]

   有些文章认为第二项是一个正则化项，防止后验分布与先验分布之间有过大差距

Proof of ELBO¶

接下来就需要做一件重要的事：证明最大化 ELBO 能够帮助我们获得最优解，即最大化对数似然。有了这个证明才能说明上述\(q_\phi\)建模的合理性，否则优化 ELBO 就是无用功。这个结论并不显然，因为 ELBO 只是一个下界，其与真实的对数似然还相差一个 KL 散度。当我们在最大化 ELBO 的时候，KL 散度会如何变化？其变化是否会影响我们的优化？可以参考 bilibili-EM algorithm 中利用（广义） EM 算法证明优化 ELBO 是合理的。这里我给出我自己的理解：

1. 如果 ELBO 是极大值，那么此时 KL 散度必定为0。这是因为等式左侧的对数似然不包含参数\(\phi\)，所以对其偏导为0，如果固定\(\theta\)，则当 ELBO 增大时，KL 散度一定减小；ELBO 减小时，KL 散度必定增大。利用反证法，如果 ELBO 是极大值，且 KL 散度不为零，那么我们可以通过更新\(\phi\)找到更小的 KL 散度，此时 ELBO 将继续增大，与 ELBO 为极大值矛盾。
2. 如果 ELBO 为极大值，则有 KL 散度为 0，那么此时对数似然等于 ELBO，即对数似然也为极大值，证毕

以上证明给为何优化 ELBO 是合理的提供思路，并不严谨，详细证明仍需要研读 EM 算法

Misc Questions¶

• 为什么去优化 ELBO 而不去直接优化\(\ln p_{\theta}(x) = \ln \mathbb{E}_{z \sim q_{\phi}(\cdot|x)} \left[ \frac{p_{\theta}(x, z)}{q_{\phi}(z|x)} \right]\)​

  这是一个小插曲，但是花费了我大量的时间来进行询问 DeepSeek，以获得正确的理解

  主要原因有两个：

  1. importance weight\(\frac{p_{\theta}(x, z)}{q_{\phi}(z|x)}\)​ 会作用到梯度之上，这会带来极大梯度方差，在训练时梯度会极其不稳定

     • High variance means the gradient estimates fluctuate wildly across different samples (unreliable updates).
     • Low variance means the estimates are consistent across samples (stable training).

     \[ \nabla_{\theta, \phi} \ln p_\theta(x) = \frac{\nabla_{\theta, \phi} \mathbb{E}_{q_\phi} \left[ \frac{p_\theta(x, z)}{q_\phi(z | x)} \right]}{\mathbb{E}_{q_\phi} \left[ \frac{p_\theta(x, z)}{q_\phi(z | x)} \right]}. \]

     Using MC sampling and reparameterization:
     - Denominator: Estimate\(\mathbb{E}_{q_\phi}[p_\theta(x, z) / q_\phi(z | x)] \approx \frac{1}{N} \sum_{i=1}^N \frac{p_\theta(x, z_i)}{q_\phi(z_i | x)}\), where\(z_i = g_\phi(\epsilon_i)\).
     - Numerator: Compute\(\nabla_{\theta, \phi} \mathbb{E}_{q_\phi}[p_\theta(x, z) / q_\phi(z | x)] \approx \frac{1}{N} \sum_{i=1}^N \nabla_{\theta, \phi} \frac{p_\theta(x, z_i)}{q_\phi(z_i | x)}\)​.

     而 ELBO 的梯度仅与建模的神经网络相关，神经网络的梯度问题已经经过了长足的优化，是相对稳定的

     \[ \nabla_{\theta, \phi} \text{ELBO} = \mathbb{E}_{\epsilon \sim p(\epsilon)} [\nabla_{\theta, \phi} (\ln p_\theta(x, z) - \ln q_\phi(z | x))], \]

  2. MC sampling 所带来的偏差

     上述对梯度的 estimator 是一个有偏的估计（biased estimator），而对 ELBO 梯度的估计是无偏估计（unbiased estimator）

     偏差的定义：对于估计量\(\hat{G}\)，如果\(\mathbb{E}[\hat{G}] = G\)​ 则认为估计量是无偏估计量。证明如下：

     目标函数的梯度为

     \[ G = \nabla_{\theta,\phi} \mathcal{L} = \frac{\nabla_{\theta,\phi} \mathbb{E}_{q_\phi}\left[\frac{p_\theta}{q_\phi}\right]}{\mathbb{E}_{q_\phi}\left[\frac{p_\theta}{q_\phi}\right]}. \]

     采样获得的梯度估计为

     \[ \hat{X} = \frac{1}{N} \sum_{i=1}^N \frac{p_\theta(x,z_i)}{q_\phi(z_i|x)},\\ \hat{G} = \frac{\frac{1}{N} \sum_{i=1}^N \nabla_{\theta,\phi} \frac{p_\theta(x,z_i)}{q_\phi(z_i|x)}}{\hat{X}}. \]

     估计量的期望为

     \[ \mathbb{E}[\hat{G}] = \mathbb{E}\left[ \frac{\frac{1}{N} \sum_i \nabla_{\theta,\phi} \frac{p_\theta}{q_\phi}}{\frac{1}{N} \sum_i \frac{p_\theta}{q_\phi}} \right]. \]

     根据 Jensen 不等式有\(\mathbb{E}\left[\frac{A}{B}\right] \neq \frac{\mathbb{E}[A]}{\mathbb{E}[B]}\)，所以这是一个有偏估计。同理可以证明 ELBO 是一个无偏估计，因为 ELBO 本身就是一个期望，函数都在期望之内，所以采样所获得的估计就是无偏的

  这两个原因导致直接优化该式子是不可行的，反而去优化 ELBO 我们就能获得稳定的梯度和无偏的梯度估计

• 上述推导都仅限于单样本，为什么不使用整个数据集进行推导？

  该问题的答案和 mini-batch 随机梯度下降是一样的。如果使用 batch 大小为整个数据集，则是用整个数据集的梯度方向的平均作为更新，最终收敛到局部最优。而使用 mini-batch 不断进行迭代求解，也能收敛到局部最优。所以研究单样本的梯度推导能够作用于整个数据集的梯度推导

Variational Auto Encoder¶

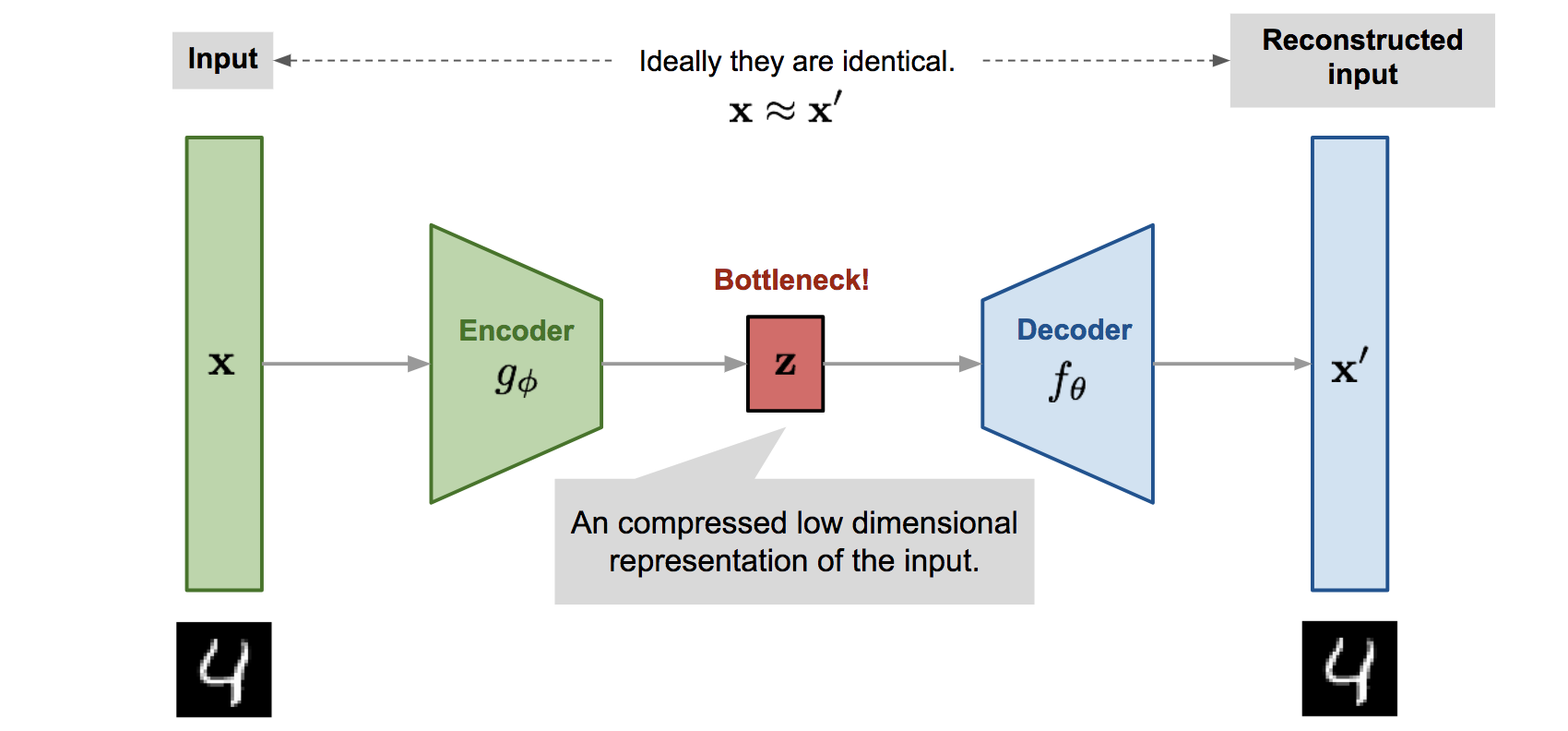
其实上述过程已经把整个 VAE 都梳理处理出来了，用下图就可以很清晰地看到自编码器的结构

这里我把 VAE 和上述的 ELBO 分析对应起来，并拿出更具体的建模和损失函数以方便理解：

• 建模后验分布\(z\sim p_\phi(z|x)\)服从高斯分布\(N(\mu_\phi, \sigma_\phi^2)\)

  Encoder\(g_\phi\)，用于生成均值和方差\(g_\phi(x)=(\mu_\phi,\sigma_\phi)\)

• 建模似然分布\(x\sim p_\theta(x|z)\)服从高斯分布\(N(\mu_\phi, \sigma^2)\)

  Decoder\(f_\theta\)，用于生成均值\(f_\theta(z) = \mu_\theta\)​，方差为常量，并不是我们所关心的

• 建模先验分布\(z\sim p(z)\)服从高斯分布\(N(0,I)\)

• 损失函数为 ELBO 损失函数

  \[ \mathrm{ELBO} = \underbrace{\mathbb{E}_{q_\phi(z|x)} \left[ \log p_\theta(x|z) \right]}_{\text{reconstruction}} - \underbrace{D_{\mathrm{KL}}(q_\phi(z|x) \parallel p(z))}_{\text{regulerization}} \]

  由于高斯分布带入到对数和 KL 散度中会有极大的简化，ELBO 第一项为重建项，可写为

  \[ \log p_\theta(x|z) = -\frac{1}{2\sigma^2} ||x - \mu_\theta(z)||^2 + C \]

  第二项为正则项，两个高斯分布的 KL 散度有解析表达式，可写为

  \[ D_{\mathrm{KL}} = \frac{1}{2} \left[ \mathrm{tr}(\Sigma) + \mu^T \mu - k - \ln |\Sigma| \right] \]

OK，现在所有元素都到齐了，可以愉快地用梯度下降进行优化了😋可以看到第一个重建损失就是常用的 MSE 损失函数，这里再一次看到了：在高斯分布假设下极大似然估计与最小二乘法之间的等价性

个人理解：VAE = Deep Nueral Nets + ELBO + Gradient Descent，用神经网络建模 encode & decoder，使用随机梯度下降方法优化 ELBO 损失函数来训练神经网络

在之后的 VAE 研究中，对于这个正则化项有不少讨论，例如\(\beta\)-VAE，就是给整个正则化项添加权重系数\(\beta\)​

-\(β=1\)：标准 VAE
-\(β>1\)：强调隐空间结构化，牺牲重构质量
-\(β<1\)：强调重构质量，隐空间约束放松

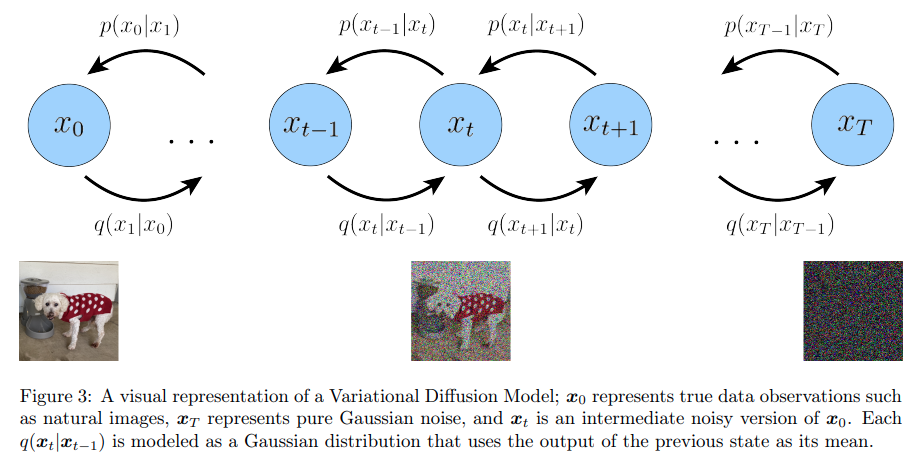
From VAE to Diffusion¶

理解了 VAE 过后再理解 Diffusion 会更加容易，需要理解几个增量的概念：

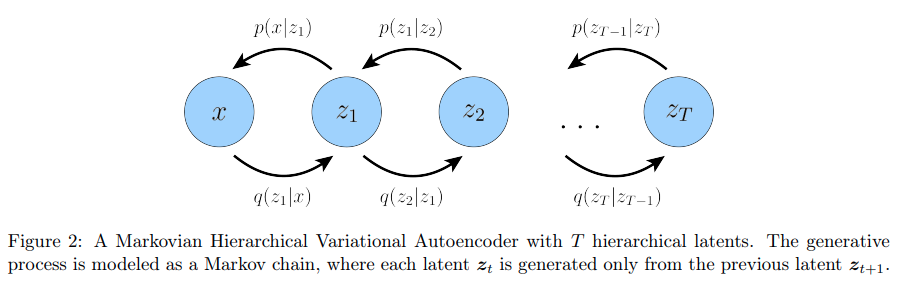
1. 引入 Markov Chain

   VAE 的推理和生成过程只有单步

   

   而 diffusion 模型则引入了 Markov Chain，让整个推理和生成过程变成多个时间步

   

2. 让推理过程\(q(z|x)\)成为一个加噪过程，生成过程\(p(x|z)\)成为一个去噪过程

   

   此时，推理过程就变得已知且简单，我们就不再需要像 VAE 一样定义一个 encoder 来进行学习，只专注于去噪过程的学习

   \[ x_t = \sqrt{\alpha_t} x_{t-1} + \sqrt{1 - \alpha_t} \epsilon_{t-1}\\ q(\boldsymbol{x}_t | \boldsymbol{x}_{t-1}) = \mathcal{N}(\boldsymbol{x}_t; \sqrt{\alpha_t} \boldsymbol{x}_{t-1}, (1 - \alpha_t) \mathbf{I}) \]

\(\sqrt a_t\)和\(\sqrt{1-\alpha_t}\)的缩放是为了保持总体方差一致，一致性可在\(x_{t-1}\sim \mathcal{N}(\mu,1)\)时得到验证：加入噪声过后，\(x_t\)的方差仍然为 1

增加了以上建模过后，理解 diffusion 就只剩_~简单的~数学推导了，我也不仔细整理了（也整理不了😅），仅留一些关键思路。经过一系列爆推，论文将 diffusion 建模下的 ELBO 化简为三项：

• reconstruction term，和 VAE 一样的重建项
• prior matching term，和 VAE 一样的正则项，并且这里\(q\)是没有参数的，\(x_T\)本身也是一个纯噪声（在建模假设下），所以该项基本为0
• denoising matching term，是重点优化的对象

值得一提的是，推导还有其他的形式，不过那种形式的 MC sampling 的方差过大，不好优化。之后就是推导\(D_{\mathrm{KL}}(q(\boldsymbol{x}_{t-1} | \boldsymbol{x}_t, \boldsymbol{x}_0) \parallel p_{\boldsymbol{\theta}}(\boldsymbol{x}_{t-1} | \boldsymbol{x}_t))\)的具体表达形式，然后将其最小化。这两个分布在我们的模型假设下都为高斯分布，所以可以直接套用两个高斯分布的 KL 散度公式

最后发现，我们只需要将这两个分布的 mean 优化得越接近越好就行，\(\mu_q\)是没有参数的，其表达式为

所以直接建模\(\mu_\theta\)为相同形式

所以最终的优化目标为

在实际应用过程中，通常去预测的是噪声\(\epsilon\)而不是\(x\)本身，所以将\(\mu_\theta\)改写为与噪声相关的形式，并给出新的优化目标

这就是 DDPM 中的所以算法了！可以看到第一项就是 sampling algorithm 的核心，而第二项就是 training algorithm 的核心。最后我们还遗留了第一项 reconstruction term 没有考虑，实际上这一项的优化目标和 denoising 的优化目标是一致的，所以二者可以进行合并，写作一个目标函数

Question¶

• 为什么在 inference 采样的时候还要加入随机噪声？

  采样，这是由高斯分布的模型假设决定的

• Markov Chain Monte Carlo (MCMC)

  在 diffusion 中使用了 Markov chain & Monte Carlo sampling，但是并没有同时使用 MCMC 方法，要学习 MCMC 可能还得在新的分支领域

• 为什么在 DDPM 中有两种不同的推导方式？为什么前者的方差较大？如何证明其方差大？