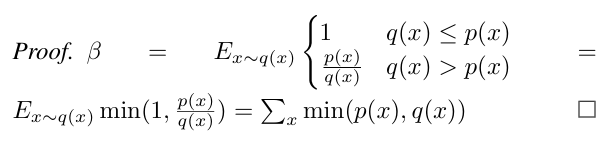Skip to content

EAGLE Speculative Decoding From Zero to Hero

约 4488 个字 62 行代码 17 张图片 预计阅读时间 23 分钟

EAGLE 投机采样作为目前 SOTA 的投机采样方法，值得整理一番。我将从投机采样基础开始，逐步地讲解 EAGLE½/3 投机采样的改进过程。相信你在读完本问过后会对 EAGLE 投机采样不再感到疑惑

Reference github

投机采样基础

LLM decode & the challenge

LLM 在 decode 阶段采用的是自回归式 decode，这样的方式每次 input tokens 数目只能为1，然后获得 next token，以此循环往复直至遇到 end of text token。用简洁的伪代码可以表示为如下

Python
# decode_token is a single integer (1,)
while True:
    # llm forward
    hidden_states = transformer(decode_token_id)
    logits = lm_head(hidden_states)

    # sample next token
    next_token_id = sampler(logits)

    # check end
    if next_token == end_of_text_token:
        break

    # continue
    decode_token_id = next_token_id

这样的方式有一个明显的问题：整个过程计算强度低，成为 memory bound 场景。一个更形象的例子来说明：input tokens = 8 和 input tokens = 1 的 decode 时间是非常接近的，因为此时计算基本上不耗时，耗时的是读取/写入权重和激活值

Core of Speculative Decoding

投机采样的核心思想，就是用一个 draft model 去猜测（speculate）后面的 tokens 是什么，猜完过后用原模型（本文有时候也会称原模型为 base model）去进行验证，如果猜对了，那就正好接受；如果猜错了，就扔掉猜错的 token。加速效果来自于并行计算了多个 input tokens，猜对得越多，加速越明显。具体来说：投机采样少量的 draft model 猜测时间 + 用一次 decode 的时间用于验证，输出了多个正确的 next tokens，所以节省了多次 decode 的时间，获得了加速效果

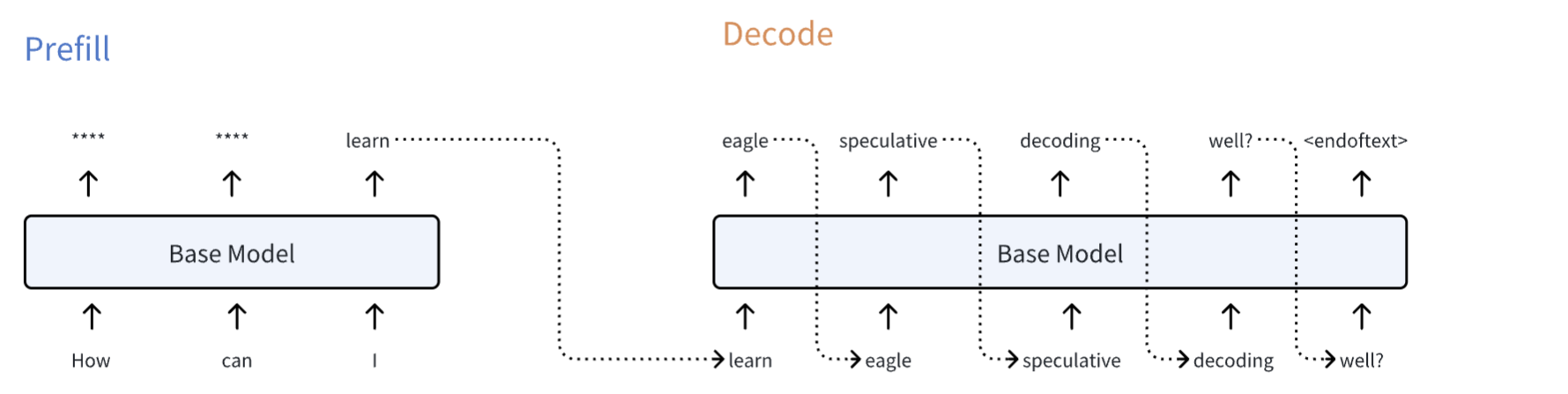
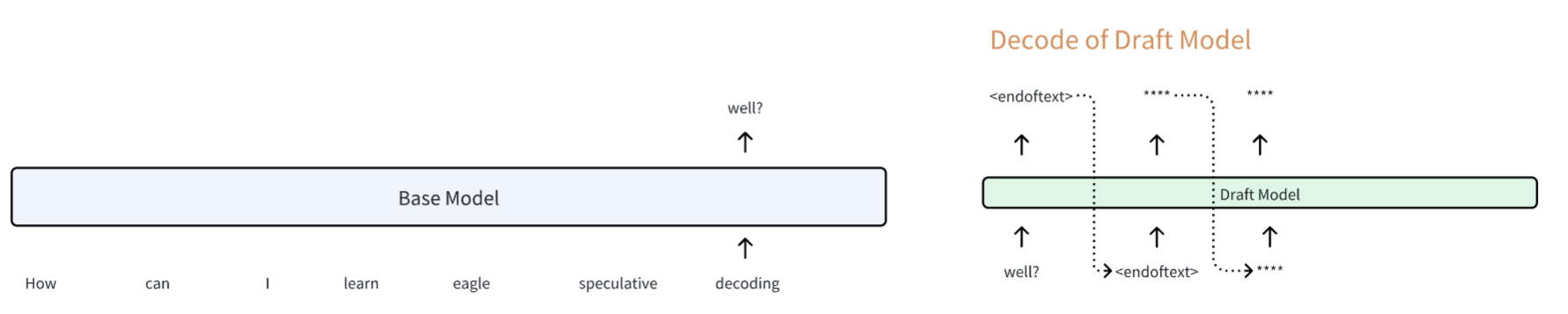
下面我将用一个具体的例子，来展示整个投机采样的过程。假设 prompt 为三个单词：How can I，并且假设 LLM 最终的 decode 输出为 learn eagle speculative decoding well?，我用以下图示来表示一般的 LLM decoding 过程

image-20250328225651677

我们可以简单地把 LLM (i.e. Base Model) 看作是一个 next token prediction machine，也就是说你给进去任何 token，它都会基于历史状态来预测下一个 token 是什么。这个想法将会简化 LLM 模型，帮助我们理解整个 speculative decoding 过程。简要描述下上图的过程：在 prefill 中输入 How can I 预测出了 3 个 next tokens，但是我们只关注最后一个，即由 I 预测得到的 next token learn。然后进入 decode 阶段，我们使用 learn 去预测得到下一个 token eagle，用 eagle 去预测得到 speculative，...，如此循环下去获得最终完整的句子 How can I learn eagle speculative decoding well?

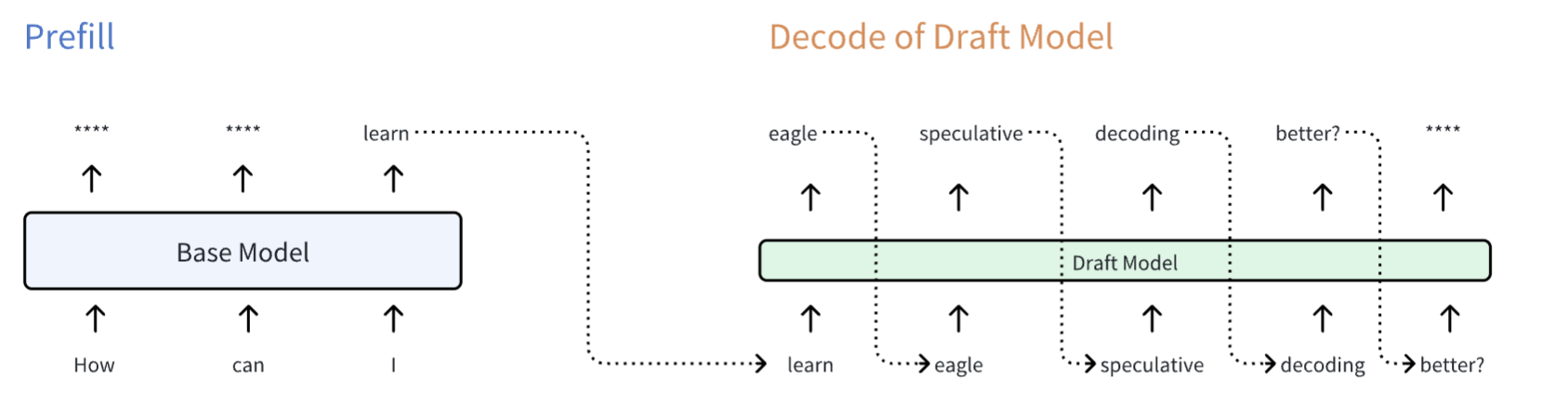
OK，现在来看看用投机采样整个过程可能是什么样的？这里就开始引入 draft model 了，该 draft model 也是一个 LLM，只不过比原来的 baes model 要小很多，但是不妨碍其本质是一个 next token prediction machine

image-20250328231636101

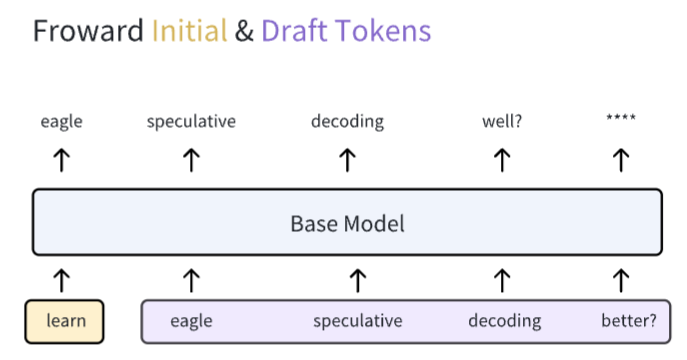
Draft model 拿到一个初始的 token learn，开始了自己的自回归过程，获得了许多 draft tokens eagle speculative decoding better? ...。这些 draft tokens 就是 draft model 去猜测 base model 接下来会生成的词。问题来了，怎么知道 draft model 猜得对不对呢？这就需要一个验证过程。验证过程的第一步就是将这些 draft tokens 连同 initial token 一起输入到 base model 中，如下图所示

image-20250329002507107

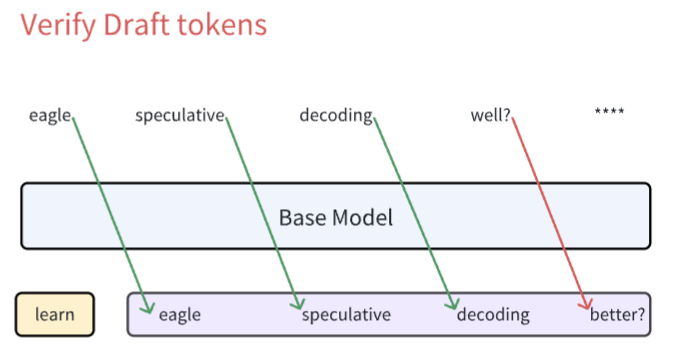
当这些 tokens 输入到 base model 过后，每一个 token 都会产生自己对应的 next token（再次强调，base model 的本质是一个 next token prediction machine）。此外你可以注意到这个图中没有虚线进行连接，这表示该过程并非自回归的，而是并行的。现在我们有了 base model 预测的 next token，我们就可以和由 draft model 所产生的 draft tokens 进行对比，看下是否猜对了

image-20250329002637632

可以看到，绿色的线条代表我们的 draft tokens 和真实的 base model 所预测的 next tokens 是一样的，红色线条就代表二者并不匹配。所以说在这个 case 当中 draft model 猜对了三个词 eagle speculative decoding。但是最后一个词 well?没有猜对，猜的是 better?，并且一旦一个词猜错过后，后面的所有 draft tokens 我们都认为是错误的，所以直接忽略掉

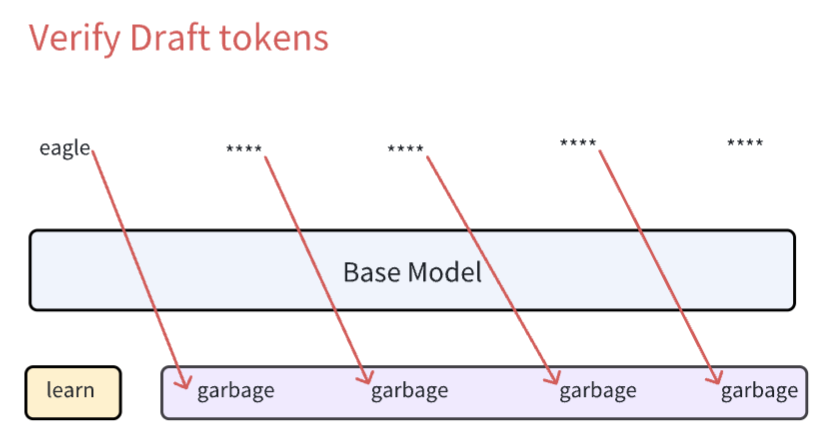
虽然最后一个词没有猜对，但是由于 decoding 这个词是猜对的，那么由 base model 预测得到的 well? 就是正确的 next token。正是这个性质，保证了投机采样的下限就是：一定获得一个正确的 next token。这种情况我用下图表示

image-20250329002706795

可以看到，即使 draft tokens 生成的是 garbage 导致一个都对不上。但由于 learn 这个词是 initial token，由 base model 正常生成，所以 eagle 这个词一定是正确的 next token

注意：在完成了 verify 过后，我们需要将正确的 tokens 进行接收，错误的 tokens 进行删除。这里主要是对 KV Cache 进行操作，将错误的 KV Cache 进行删除，保留正确 tokens 的 KV Cache

最后，生成还没有结束，因为我们现在获得的最新的 next token 是 well?，还没有遇到 <endoftext>，所以继续进行下一轮的投机采样：

  1. 将 initial token (well? in this case) 输入到 draft model 当中，生成 draft tokens
  2. 将 initial token & draft tokens 输入到 base model 中，生成 base model 预测的 next token
  3. 将 base model 预测的 next token 和 draft tokens 进行对比验证
  4. 如果没有出现 <endoftext> 回到 Step1

image-20250328235339912

Extend to sampling situations

在上面的讨论中，我们利用了 base model 的前向输出去验证 draft tokens 的正确性，完成这一操作有一个隐藏条件：base model & draft model 在预测 next token 的时候是确定性的，用专业术语来说就是：temperature 为 0。如果这个条件无法满足，那么上述的错位对比是没有意义的（无法对比不确定的东西）。temperature = 0 在具体实现中就是直接使用 argmax(probability) 来完成对 token 的选取

在 temperature != 0 的情况下，我们就需要通过采样来获得 next token。此时 draft token & base model 输出变为不确定性的，但我们仍然可以验证所生成的 draft token 分布是否符合 base model 应该生成的 token 分布。接下来就需要做下概率论了🤔

定义：draft token 预测 next token x 的分布为 q(x)，而 base model 预测 next token x 的分布为 p(x)

目标：从分布 q(x) 出发，最终获得分布 p(x)

算法：下图来自于 EAGLE-3 paper，描述了多 token 的投机采样算法。其核心思想是：先从 q(x) 分布中采样，以一定概率去接收采样到的 x，如果 x 被拒绝，则在一个新分布重新采样一个 x。该过程采样获得的 x 在数学上等价于直接从 p(x) 中直接采样

image-20250330223102475

我将上图的算法抽象为 python 伪代码，并只考虑 single round

Python
def speculative_sampling(p, q):
    x = sample_from_distribution(q)
    ratio = p(x) / q(x)

    r = uniform(0, 1)
    if r < ratio: # accept the x according to ratio
        return x
    if r >= ratio: # reject x, resample from a new distribution
        new_p = lambda x: (p(x) - min(p(x), q(x))) / sum([p(x) - min(p(x), q(x)) for x in sample_space])
        new_x = sample_from_distribution(new_p)
        return new_x

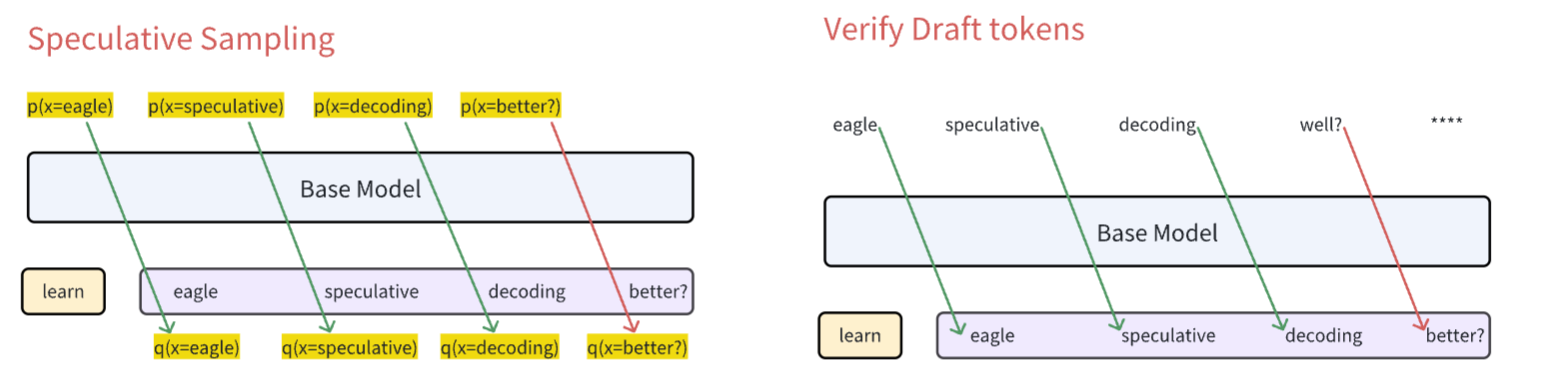
该采样过程的正确性在下面的 section 给出。现在我们重新来审视投机采样和之前的 verify 过程：左侧即为当前讨论的投机采样，而右侧即为简单的 verify 过程

image-20250330232028249

可以看到左侧， base model 没有生成 token，而是生成的对应的概率分布，我们将利用这个概率分布 p(x)，来和对应的 draft token 分布 q(x) 进行投机采样。之前的 verify 过程，变为了现在的是否接收采样结果：

  1. 若接收当前 draft token，则继续验证下一个 draft token
  2. 若拒绝当前 draft token，则用新分布重新采样，生成一个新的 token，在此之后所有的 draft token 全部舍弃

Proof the correctness

按照上述方法采样产生的 x 在数学上是等价于 p(x) 的。证明来自投机采样论文 Fast Inference from Transformers via Speculative Decoding

image-20250330224150492

上述证明中，没有提到\(\beta\)的定义，在论文中定义为：采样结果被接收的概率。采样结果被接收的概率是一个期望值，如下

image-20250330224536397

我再翻译一下这个期望：

  1. 当 q(x) <= p(x) 时，采样结果一定会被接收，概率为 1
  2. 当 q(x) > p(x) 时，采样结果以概率 p(x) / q(x) 接收

EAGLE-1 Chain

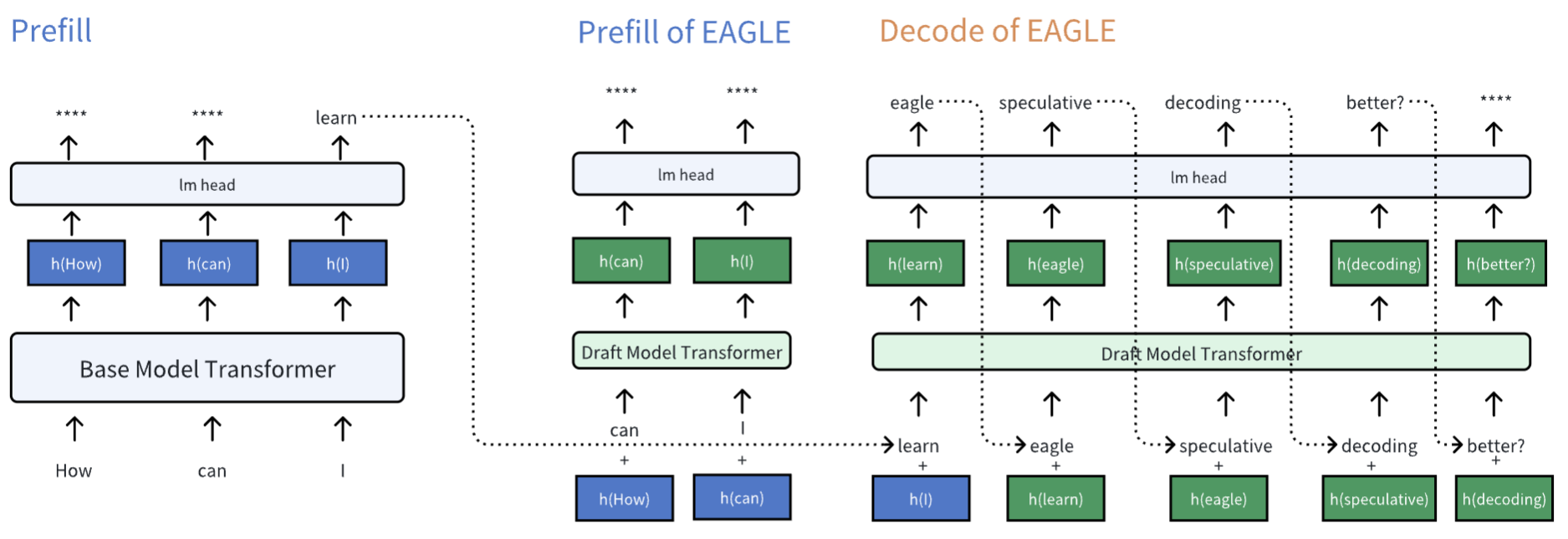
第一章节的投机采样原理是“神”，而其他的方法都是“形”。对于 EAGLE 来说，其特色就是在 draft tokens 生成过程中，加入了 hidden_states 作为额外的信息，来帮助 draft model 更好猜测。

image-20250401223536273

在上图中使用深色方块来表示 hidden states，并且用不同颜色标记该 hidden states 是来自于 base model 还是 draft model。图示仅描述了第一次 eagle decode 做了哪些事情：

  1. 使用 input tokens & hidden states 完成 EAGLE prefill。可以看到 input tokens 和 hidden states 在 EAGLE prefill 时是有一个位移的，所以第一个 token 无法进行 EAGLE prefill，因为缺少对应的 hidden states
  2. 用 base model prefill 所产生的第一个 initial token 以及对应的 hidden states 来开启 EAGLE decode

之后就是 verify draft tokens，并删除 base model 中错误 token 的 kv cache，而对于 draft model kv cache 而言有两种选择：

  1. 和 base model 一样，删除错误的 kv cache 即可
  2. 清除掉本轮 decode 除了第一个 token 以外的所有 kv cache，然后重新用正确 token 的 base model hidden states 生成新的 draft model kv cache

选择2在 EAGLE 中被称为 stable kv，其确保在 decode 之前，draft model 中的 kv cache 全部由 base model hidden states （深蓝色方框）生成。而选择1则会保留由 draft model hidden states （深绿色方框）产生的 kv cache，这就造成了 kv cache 来源的混合（我称为 unstable kv）。这两个选择这为 EAGLE-3 埋下了伏笔：选择1无需进行新的 prefill，虽然节省了时间，但是投机命中率会下降。原因在于：训练时 draft model 全部都是在 stable kv 的情况下训练的，如果使用 unstable kv 会让误差在长序列中持续累积，影响预测效果

为了命中效果，我们选择 stable kv。并将 verify draft tokens & stable kv cache 的图示表示如下

image-20250401223604049

EAGLE-2 Tree

EAGLE-2 对于 EAGLE-1 的改进在于将 draft model 从 Chain 模式改为 Tree 模式（实际上 Tree 模式是 Medusa 率先提出，EAGLE-1 也采用了 Tree 模型，EAGLE-2 是对 Medusa Tree 模式的改进）

  1. Chain 模式就是一般的 auto-regressive 过程，每一次根据 logits 只 sample 出一个 token，
  2. Tree 模式则在每一次 auto-regressive 过程中，每一次根据 logits 会输出多个 token，通常用 topk 来找概率最高的 k 个 token

Tree 模式的 intuitive 来自于：每一次多猜几个 token，通过多种可能的组合（而不是一种），来提高命中的概率。不过这样的过程设计到对 kv cache & mask 的复杂管理，以及需要使用 tree attention，二者都会有较多的 overhead。所以 Tree 模式在实际使用中会比较少见，该部分内容将不会整理得非常详细

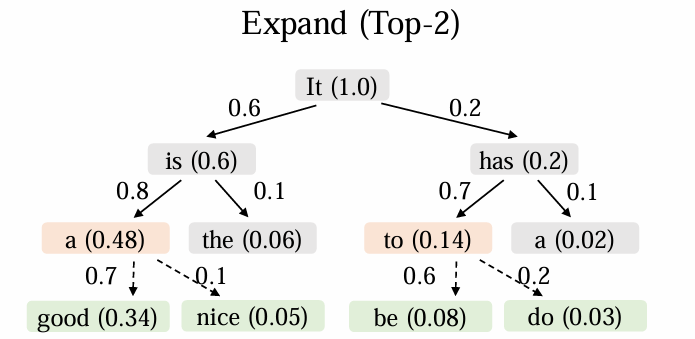
以论文中的 Topk = 2 为例子，看下在生成 draft tokens 时是如何一次输入&输出多个 token 的

image-20250401223737838

一行一行的看：

  1. input token It，initial token，很好理解，其得分为 1。通过其 logits 生成第二行
  2. input token is & has，是通过 logits 中选出来的 top2 token，他们对应的概率为 0.6 & 0.2，每一个节点的累计得分为它的概率乘以其父节点的得分，所以其累计得分为 0.6 和 0.2
  3. input token a & the & to & a，通过第二行选出的各自 top2。在这一行中，需要对 4 个 token 排序，从中选出新的 top2，该 top2 token 作为父节点，生成下一行
  4. input token good & nice & be & do，从第三行中的 top2 生成的各自 top2。依然对 4 个 token 排序，从中选出新的 top2，该 top2 token 作为父节点，生成下一行
  5. 循环 4

可以看到，每一次都是动态地去选择每个 depth 可能性最高的 token 作为父节点，然后去生成接下来的 draft token，这样就能最大概率地增加投机命中率

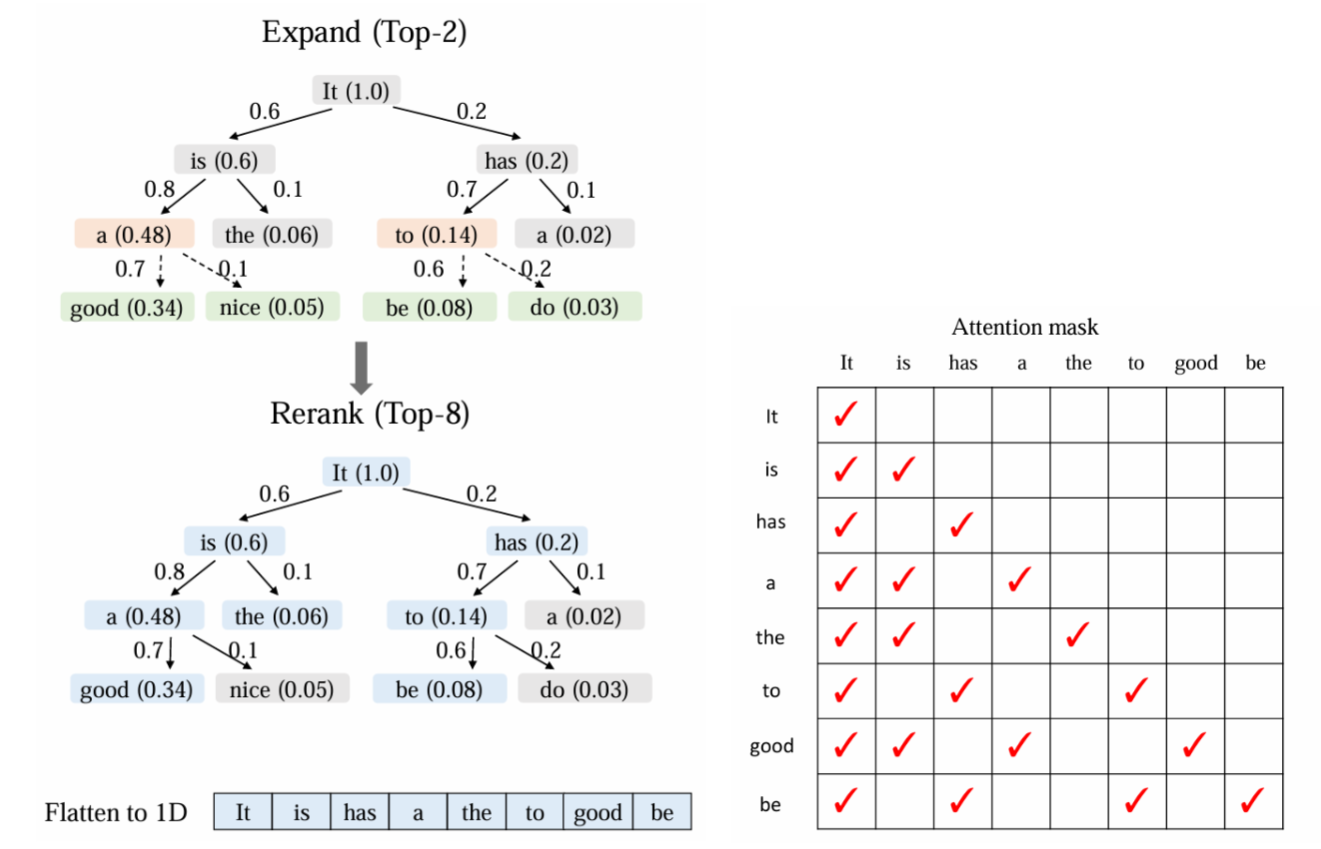
不过问题来了：在进行前向计算中，由于各个 token 只会和自己父节点进行 attention 交互，对于其它节点是不会进行 attention 计算的。所以每次 input token 需要搭配正确的 attention mask 才能获得正确 kv cache & 输出

一般来说 transformer 会自动帮忙生成 causal mask 来进行 attention 计算。所以我们只需要将精力集中在非 causal 的部分，然后将非 causal 的部分替换即可

image-20250401223824092

每一行就代表了一次 draft model 进行了一次 forward，每一次（除了第一次）都是输入了两个 token。可以看到这两个 token 之间不会进行注意力交互，所以 mask 一定是 identity matrix（图中蓝色虚线所示）。而每一个 token 都会和自己的父节点注意相同的内容，所以会直接继承父节点的 mask（图中红色虚线所示）。以上两个规律就能每次快速构建 input attention mask 来进行前向计算

上述阶段是 EAGLE-2 论文中的 Expand 阶段，该阶段已经在尽可能地生成投机命中率较高的 token，但 tokens 仍然很多，且不是所有 token 都具有不错的潜质，例如一些深层的 token 其命中概率已经很低了，不如多选一些浅层的 token 来提高命中率。所以我们对所有的 draft tokens 根据其累计得分进行排序，再选出 topk 个 tokens，这就是最终会输入到 base model 进行验证的 tokens。在输入到 base model 中去时，仍然需要一个正确的 attention mask，该 attention mask 保证了 token 只会注意到自己的父节点 tokens

image-20250401224639668

相比于 generate topK 当中的 attention mask，这里面多出了 the token，the token 没有被选中作为父节点来生成子 token，但是其命中概率仍然较高，所以被选入最终的 draft token 进行验证

EAGLE-3 Train

在之前的 EAGLE-1 Chain 中我就埋下了伏笔：EAGLE 在训练当中只看到了 stable kv 的情况，也就是其所使用的 hidden states 全部来自于 base model。但是 EAGLE 在推理的时候大部分 hidden states 其实都来自于 draft model 本身产生的 hidden states。这也是为什么 EAGLE 在训练的时候需要对 draft model hidden states 进行监督，让其尽可能地去复原 base model hidden states，这样在推理的时候尽可能还原训练场景

EAGLE-3 就发现：如果不对这个 hidden states 进行监督，第一个猜测的 token 的命中率会随着数据集增加而显著提升，但是第二个猜测的 token 命中率就急剧下降了。总结其中原因：

  1. 去除 hidden states 监督进行约束，则只有 next token prediction 监督，使得 next token prediction 能力增强，并且具有 scaling 性质。但该情况只存在于第一个猜测 token。反之，保留 hidden states 监督进行约束，将影响 next token prediction 的学习，掩盖了 scaling 性质
  2. 第二个猜测 token 使用的 hidden states 是由 draft model 产生，属于 unstable kv 情况，在训练中没有见到过，命中率急剧下降

于是乎，解决方法呼之欲出：在训练 EAGLE 时，加入 unstable kv 情况，这样就能将 train & test 情况进行统一，然后去除 hidden states 监督，拿到 scaling 收益

image-20250401224702909

另外 EAGLE-3 使用的 base model hidden states 有多个，来自于不同 layer，用于表征 high & middle & low feature，这个技巧也是非常有用的。最后论文里写的这句话还挺有意思的

Interestingly, EAGLE inspired the multi-token prediction technique used in the pre-training of DeepSeek v3 (Liuetal., 2024a), which in turn inspired new architectural designs in EAGLE-3.

然后我就去看了 DeepSeek-V3 的 Multi-Token-Prediction，看上去和 EAGLE-1 的思路会比较像，但是和 EAGLE-3 的思路相差甚远：

  1. DeepSeek-V3 在论文中明确提到了 complete causal mask，这不不像 EAGLE-3 当中的特殊 mask，更像是 EAGLE-1 Chain 当中的正常 causal mask
  2. DeepSeek-V3 所使用的 input tokens 为真实数据，而 EAGLE-3 在进行第二个 training step 的时候已经开始使用 draft model 所产生的 token。或许这里像 DeepSeek-V3 一样使用 ground truth input tokens 会更好
  3. DeepSeek-V3 讨论的是多个 module 来预测多个 next token，而 EAGLE-3 仍然是使用一个 draft model 来生成多个 next token

update 2025/07

对于 mtp & eagle decode 之间的联系与区别：Mtp 通过 mtp module 让 main module 对未来多个 token 进行理解，此对训练的稳定非常重要。Eagle3 通过自回归让自己对未来多个 token 进行理解与预测，同时解决了 feature estimation 问题。mtp 当然也可以采取同样的做法，但是主模型进行自回归的代价太大了，使用 mtp 小模型来进行辅助是更合理的选择

Flex Attention

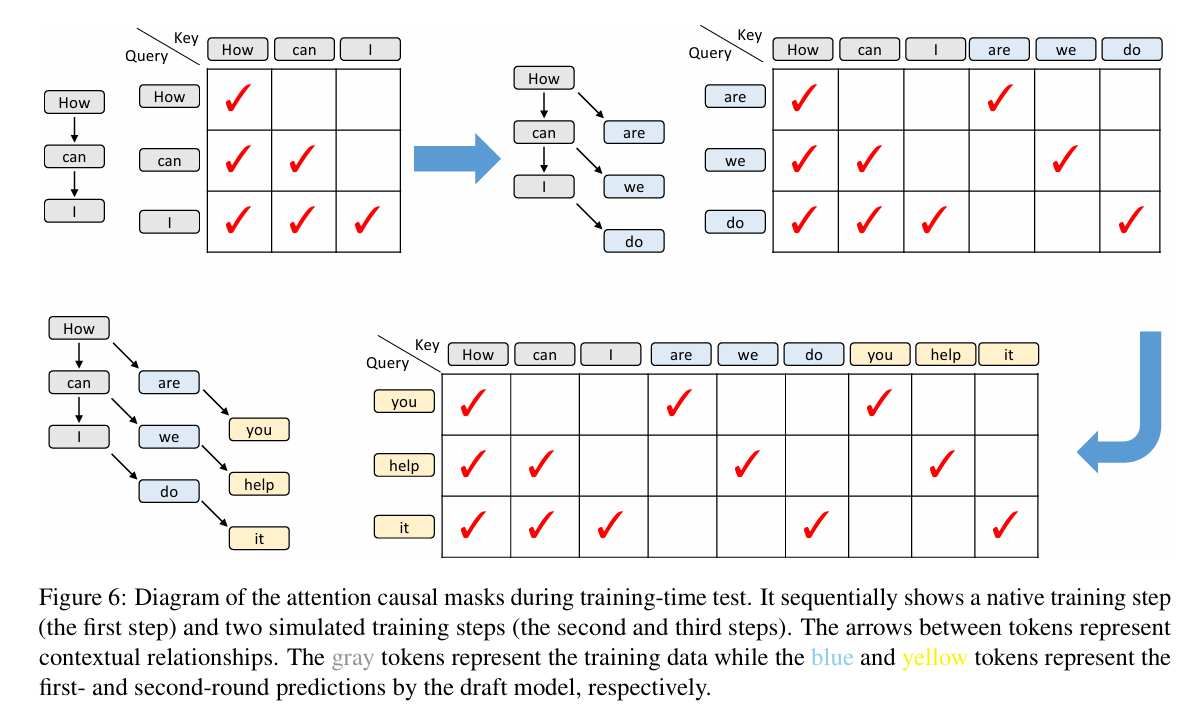
由于 EAGLE3 使用了 ttt 训练策略，所以 attention mask 形成了一个稀疏矩阵。在 EAGLE3 论文当中提到

Using matrix multiplication in this case would result in significant computational waste, so we can use vector dot products to calculate the attention score only for the corresponding positions.

所以其 attention 计算分为了两个部分，一个是 causal mask 使用 sdpa，另一个是 dot product 计算 diagnal attention。这样会让 attention 表达变得复杂，而且显存并没有实质性的节省。而 flex attention 提供了一个简洁且节省显存的 attention 计算方法。根据 EAGLE3 代码可以写出如下 mask 计算模式

Python
from torch.nn.attention.flex_attention import or_masks
def generate_eagle3_mask(
    seq_lengths: torch.Tensor, Q_LEN: int, KV_LEN: int, shift_left: int = 0
):
    # seq_lengths: (B,) acutal lengths of each sequence
    def causal_mask(b, h, q_idx, kv_idx):
        # Causal will keep shrinking by 1 diagnol due to appended suffix
        # Shirnk the causal by diagnol
        causal_mask = (q_idx - shift_left) >= kv_idx
        padding_mask = kv_idx < seq_lengths[b]
        return causal_mask & padding_mask

    def suffix_mask(b, h, q_idx, kv_idx):
        suffix_mask = kv_idx >= Q_LEN
        padding_mask = kv_idx % Q_LEN < seq_lengths[b]
        diagnol_mask = (kv_idx - q_idx) % Q_LEN == 0
        return suffix_mask & padding_mask & diagnol_mask

    mask_mod = or_masks(causal_mask, suffix_mask)
    mask_mod.__name__ = f"eagle3_mask_Q_{Q_LEN}_KV_{KV_LEN}_shift_left_{shift_left}"
    return mask_mod

我以 seq_len = 3 为例子，看下前面两个 step 的 attention mask 如何

Python
# step=0, Q_LEN=3, KV_LEN=3, pure causal mask
    0 1 2
0 ✅❌❌
1 ✅✅❌
2 ✅✅✅
# step=1, Q_LEN=3, KV_LEN=6, causal mask & suffix mask
    0 1 2  1 2 3
1 ❌❌❌ ✅❌❌
2 ✅❌❌ ❌✅❌
3 ✅✅❌ ❌❌✅
# step=1, no causal shift mask, should we use this?
    0 1 2  1 2 3
1 ✅❌❌ ✅❌❌
2 ✅✅❌ ❌✅❌
3 ✅✅✅ ❌❌✅

可以看到 causal mask 在逐渐减少，这和 EAGLE3 论文描述是不符合的，issue 对此提出疑问，不过没有得到官方的回复。

在 flex attention 文档中有很多关于 torch.compile 相关的问题，在实际使用中似乎不考虑 compile 会让编程更简单，或许以后的 torch version 都会自动考虑这个问题。推荐 torch>=2.6 的版本，flex attention 会更好用