From SmoothQuant to SVDQuant¶
约 3201 个字 2 行代码 8 张图片 预计阅读时间 16 分钟
本文将从一个统一的理论分析,对三个量化方法进行总结:SmoothQuant & AWQ & SVDQuant。这三个方法均来自于 MIT Han Lab,所以这三个方法能统一起来也不奇怪。希望通过文本,能够让大家理解大模型量化的常用形式与基本原理
量化基础¶
什么是量化?其本质是用低比特数来表示高比特数,这将带来硬件上带宽和计算的成倍优势:低比特传输数据成倍减少,同时低比特运算速度成倍增加。我们通常在实践中使用的 int 对称量化公式如下
其中:
- \(\Delta\)就是量化中常说的 scale
- \(Round(\frac{W}{\Delta})\)就是我们需要保存的量化数值,\(W\)既可以是权重也可以是激活
- \(Q(W)\)为反量化过后的浮点数
还有一点再解释一下:为什么是用\(2^{N-1}-1\)作为\(\Delta\)的分母?而不使用\(2^{N-1}\)?
以 int8 为例子,该分母算出来为 127,而不是 128。这说明 scale 将浮点数缩放到了 -127~127 这个范围中,一共有 255 个可选数值。如果我们直接使用\(2^{N-1}\)作为分母,则会将浮点数缩放到 -128~128 范围,这样一共有 257 个数值需要表示,超出了 int8 的表示范围
对于 fp8 量化来说过程也是类似:先将高比特浮点数缩放到低比特能够表示范围内,然后利用 round to nearest 获得低比特数值
此时一个高比特浮点数需要两个数值来表示:一个高比特的浮点 scale,和一个低比特数值。似乎量化并没有为我们节省什么,这又多出来一个高比特的 scale。然而在量化过程中,通常有一大批数值都需要量化,我们可以让一批数值共享同一个高浮点 scale(例如每 128 个数值共享一个 scale),这样就节省了 scale 开支,绝大部分的数值表示都是以低比特形式存在
此时有一个重要的结论需要给出:对于一组需要量化的数值中,如果其中存在异常值(outlier)显著地比其他数值要大,那么其量化误差就会非常大。这也不难理解,以 int 量化为例,异常值导致了 scale 的计算结果很大,数值与数值之间的差异必须以 scale 的整数倍存在,要么大家都是相同数值,要么大家差别很大
LLM 量化误差分析¶
前提:在深度学习中,由于模型的层数可以非常深,所以想要对一整个网络进行误差分析是相当困难的事情。绝大部分的量化误差理论分析都仅限于对单个矩阵乘法当中。如果想要考虑多个网络层,可能用 QAT 的方式进行端到端的训练才是可行的方法。以下理论分析整理自 SVDQuant
矩阵乘法量化误差的定义
为了方便描述,定义上述矩阵的形状:X.shape = (m, k) & W.shape = (k, n)
Frobenius 范数定义
SVDQuant 利用缩放得到了量化误差的一个上界,如下所示
证明过程如下,本质上利用了三角不等式和柯西不等式
我们去优化此上界就能够优化量化误差,而该上界由2个关键因素限制
- activation & weight 的 F-范数大小
- activation & weight 的量化误差大小
对于 activation & weight 的量化误差,几乎是无法消除的,这是由于 round 操作的天然属性。所以降低 activation & weight 的 F-范数大小成为了降低矩阵乘法量化误差的关键
SmoothQuant-W8A8¶
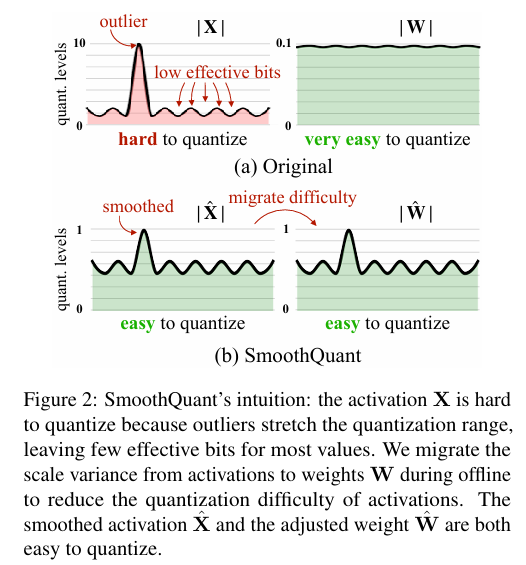
SmoothQuant 论文的核心结论:
-
activation 异常值过大,导致量化误差很大,但是 weight 的异常值较少
-
activation 异常值分布不是随机的,而是在在某些固定 channel。通过缩放因子\(s\),把 activation 的异常值,转移到权重上,同时保持运算的等价性。
\[ Y=(X·diag(s)^{-1})·(diag(s)W)=\hat{X}\hat{W} \]
我们仍然从上述得到的误差上界来分析
SmoothQuant 将其中的\(X,W\)替换成为了\(\hat{X},\hat{W}\),降低了 activation 的 F-范数大小,也通过减少异常值来减少 activation 的量化误差。需要注意的是:
- 此缩放会增加权重 F-范数大小,所以上述公式的第二项一定会增加,但是相比第一项占比很少,所以影响不大
- 此缩放会增加权重当中的 outliers,从而导致权重量化误差\(\|\boldsymbol{W} - Q(\boldsymbol{W})\|_{F}\)显著增加,不能够无限制地进行缩放
所以如何寻找最优的缩放因子\(s\)是 SmoothQuant 的另一贡献。方法也非常简单,以 activation 和权重作为 reference,通过格点搜索超参数\(\alpha\)来获得最优缩放因子
其中\(j\)表示第\(j\)个channel,目标函数就是量化误差
AWQ-W4A16¶
AWQ 其实就是 SmoothQuant 的 weight-only 版本,其理论分析更加简单
对于 w4a16 weight-only 量化,activation 的量化误差就不存在了,所以上式的第二项直接为零。
此时直接缩小 activation 的 F-范数将变得非常有收益,这也就是 AWQ 方法的直接体现。SmoothQuant 的缩放方式、搜索方式仍然适用于 AWQ,所以我说 AWQ 就是 SmoothQuant weight-only 版本。由于 AWQ 的情况更简单,所以在此我们还可以对误差分析做得更精确一些,比如:被缩放的权重所造成的误差到底有多大?
其中\(\text{RountErr}(·)\)可以看做一个近似于 uniform distribution\(X\sim\mathcal{U}(0,\,0.5)\)的分布函数,其平均误差为 0.25。所以当\(\Delta\)没有变化时,可以认为权重量化的误差也变化不大。但是当我们进行缩放时,是有可能改变\(\Delta\)的,其由权重缩放过后的权重最大值决定,以 int 量化为例子
当最大值放大两倍,会导致\(\Delta\)放大两倍,同时误差也会放大两倍,这也是我们为什么不能无限制地缩放 activation 的原因
SVDQuant-W4A4¶
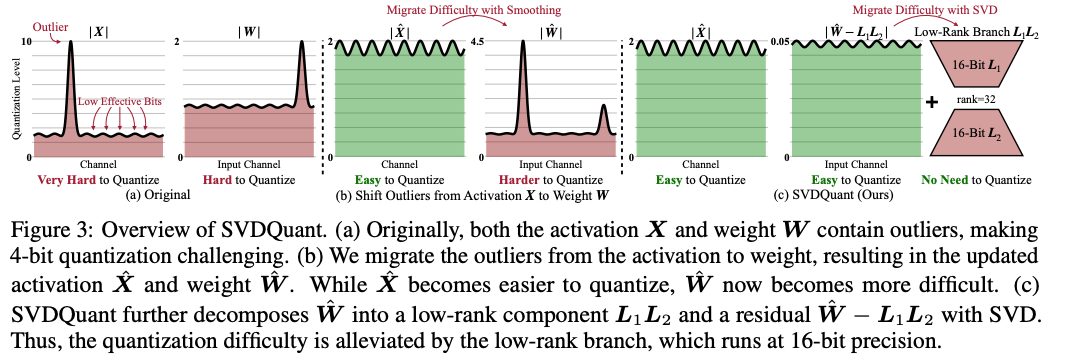
SVDQuant 比 SmoothQuant 将更加强大,其要解决 W4A4 的量化精度问题。SmoothQuant (W8A8) 会将 activation outlier 转移到权重当中,但是对于 W4A4 的量化方法,这种 smoothing 方式也将受到更多限制,因为 4-bit 权重无法像 8-bit 权重一样对 outlier 有很好的精度保证
解决思路:使用一个 low-cost branch 将这些 outlier 进行吸收。具体来说,论文先利用 smoothing 的方式将 activation 的 outlier 移动到 weight 上,然后将 weight 的 outlier 用两个低秩矩阵\(L_1L_2\)进行吸收。具体来说 weight\(W\)将被分解为两个部分:
最终得到的 residual\(R\)会是一个更好量化的矩阵。如此 activation & weight 都能够进行很好的 4-bit 量化
论文在 related work 中也提到了其他方法也使用了 low-rank 的方式来做量化,不过他们的缺陷在于没办法做出加速效果,只专注于权重压缩效果。实际上把量化模型进行加速并不简单,这就是写算子的魅力时刻🫡
SVDQuant Method¶
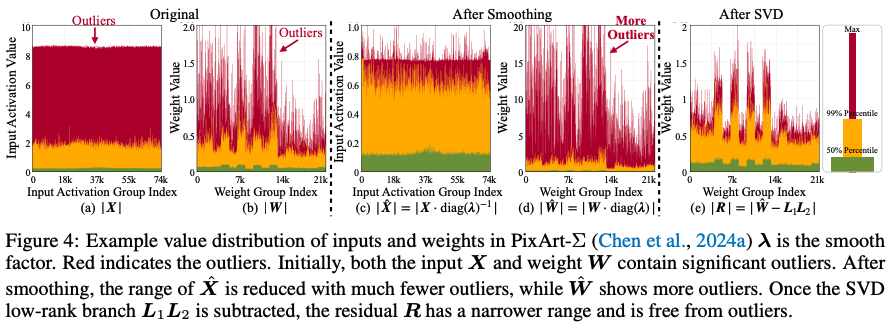
SVDQuant 首先也采用 AWQ/SmoothQuant 当中的 smoothing 方法,把 activation 当中的 outlier 转移到 weight 当中
经过放缩的 weight 现在的 outlier 也会变得比较多,论文使用一个 low-rank 分支来把这些异常值进行转移,留下一个 outlier 较少的 residual 部分
其中两个低秩矩阵的形状为 L_1.shape = (m, r) & L_2.shape = (r, k)
如此一来,矩阵乘法被分解为了两个部分:由 activation & low-rank 组成的高精度运算 + 由 activation & residual 组成的低精度运算。其中高精度运算的 tops 由于低秩的存在,会显著较低,可得其计算占比
现在我们的目标就是要找到足够好的低秩矩阵,让矩阵乘法的量化误差最低。将低秩矩阵带回原来的矩阵量化误差式子中
可以看到最终的误差从原来的\(E(X, W)\)变为了当前的\(E(\hat{X}, R)\)。此时回顾之前的矩阵量化误差分析结论:影响矩阵量化误差的2个关键因素就是 activation & weight 的 F-范数。换句话说,我们现在想要做的就是降低\(\hat{X}\)和\(R\)矩阵的 F-范数。而\(\hat{X}\)是已经利用了 smoothing 方法进行优化,论文就不做进一步的讨论,问题进一步简化为:寻找足够好的低秩矩阵,以最小化\(R\)矩阵的 F-范数大小
这个问题其实早就被 SVD (Singular Value Decomposition) 给解决了。在 SVD 的语言中,这里就是在寻找 rank=r 的\(\hat{W}\)矩阵的最优近似,即:\(\hat{W}\)矩阵的低秩近似。这里直接给出结论:\(\|\boldsymbol{R}\|_{F}\)的最小值就是\(\hat{W}\)中 i>r 的奇异值的的几何平均\(\sqrt{\sum_{i=r+1}^{\min(m,n)}\sigma_{i}^{2}}\),而低秩矩阵则表示为
至此 SVDQuant 的误差理论分析已经结束,经由 smoothing + SVD 的双重优化,降低了 activation & weight 的 F-范数,从而将矩阵乘法误差的显著降低
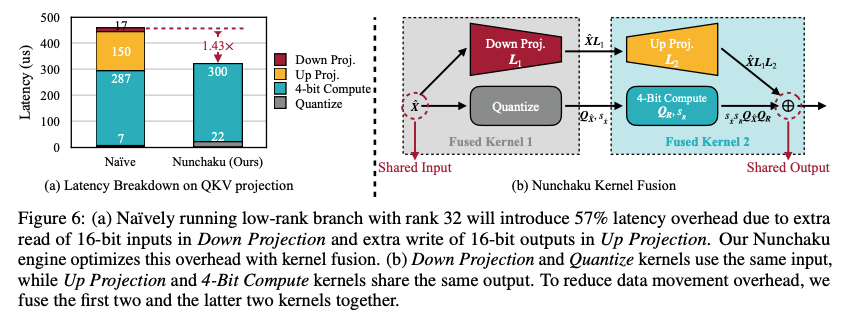
SVDQuant 算子优化¶
由于 SVDQuant 引入了低秩分支,虽然计算量少,但是输入和输出 shape 并没有改变,也需要花费大量的时间用于 memory 操作上。如果不做融合的操作,两个 branch 就会分别对输入和输出进行 memory 读取/写入,这样 memory 的操作就重复了两次。为了解决这个问题, SVDQuant 提出了 Numchaku (双截棍) Fused Kernel 的方式,只对输入和输出进行一次读取/写入,显著减少运行时间
Experiment¶
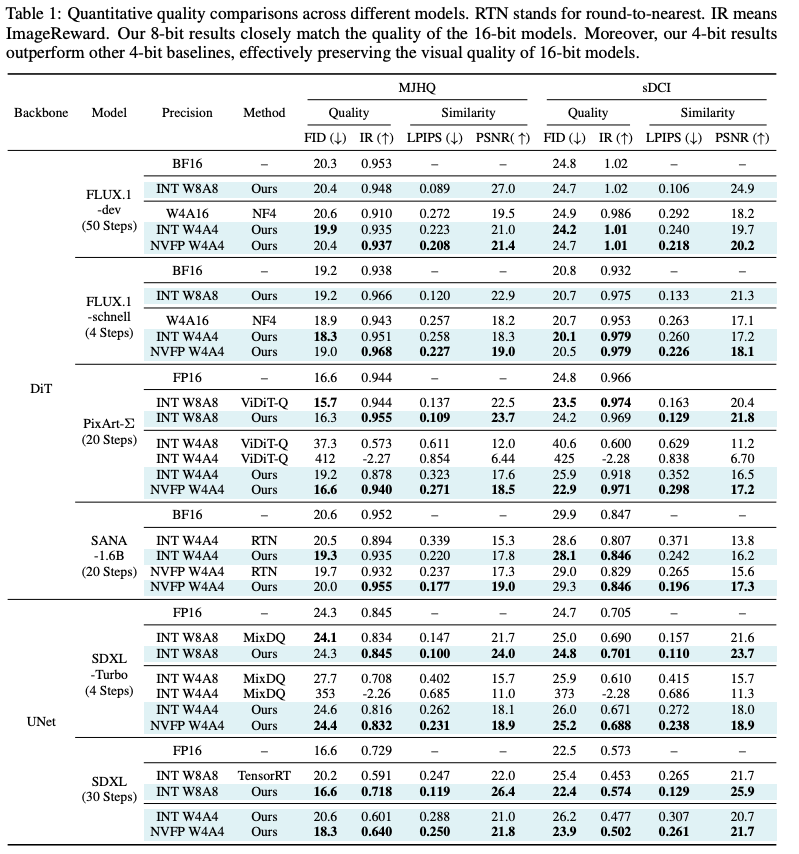
SVDQuant 应该就是受到 LoRA 领域的启发,很有可能其出发点就是想要加速 LoRA 模型。论文的实验都是用的 diffusion 模型,没有 LLM 相关的结果。在 diffusion 评价指标上,SVDQuant 的指标都很好,非常接近 fp16 模型
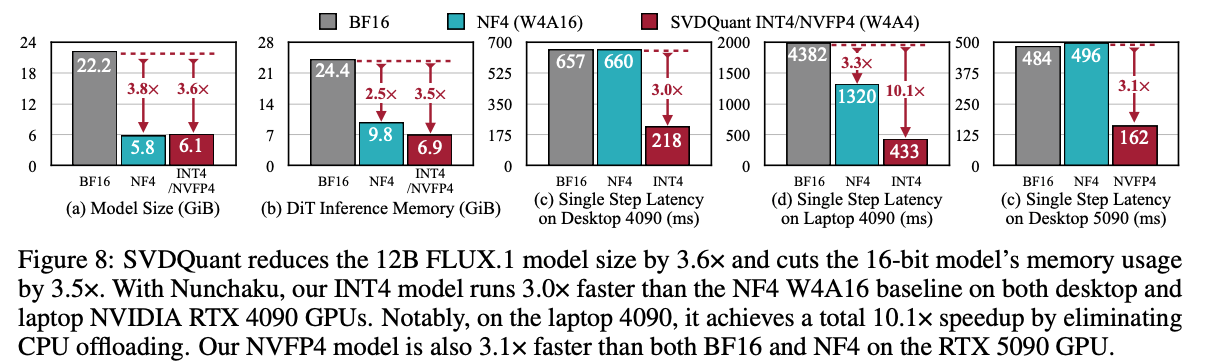
在运行效率上,能够减少 3.6x 的显存,加速 3x
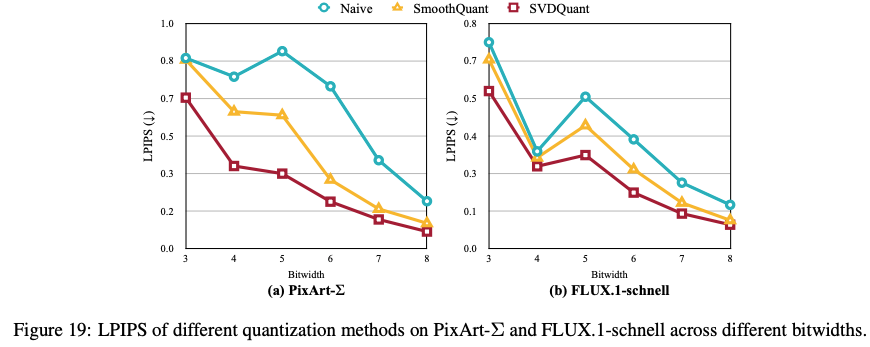
论文在附录里还和 SmoothQuant 在多个 bit-width 下进行了对比,其结果持续优于 SmoothQuant,但是在 8-bit 下对 SmoothQuant 没有显著优势
另外论文也指出对于 2-bit 量化(W2A4 or W4A2),SVDQuant 无法生成有意义的图像,一些研究也指出对于如此低 bit 的量化需要使用 QAT 的方式来大量更改 weight 的分布