GPTQ 原理以及完整证明¶

约 4164 个字 6 张图片预计阅读时间 21 分钟

2025-12-242025-12-24

GPTQ 即使提出的时间相当早（2022），但目前仍然活跃在当前（2025）的 LLM 量化方法当中，可见其强大之处。本文将对 GPTQ 的原理进行深入理解，并且对论文中的公式进行完整的证明。原论文中许多公式和结论直接一笔带过，甚至没有说明，这给论文的阅读带来相当大的难度，本文可能是全网唯一对 GPTQ 进行完整证明的文章

论文：GPTQ: Accurate Post-Training Quantization for Generative Pre-trained Transformers
论文代码：https://github.com/IST-DASLab/gptq
社区代码：https://github.com/AutoGPTQ/AutoGPTQ

前身 OBS & OBQ¶

OBS: Optimal Brain Surgeon

OBQ: Optimal Brain Quantization

OBS 是一种神经网络的裁剪方法，核心思路是：在二阶近似的条件下，寻找一些权重，将这些权重删除后对模型产生的误差最小，其简单的推导过程如下：

考虑训练到局部最小误差的网络，对于权重扰动$\delta \mathbf w$的 Loss 的二阶泰勒展开

\[ \delta E = ( \frac{\partial E}{\partial \mathbf{w}})^T \delta \mathbf{w} + \frac{1}{2} \delta \mathbf{w}^T \mathbf{H} ·\delta \mathbf{w} + O(\|\delta \mathbf{w}\|^3) \]

$E$就是网络的输出，例如：对于一个线性层来说$E=\mathbf{w}·\mathbf{x}$

其中$\mathbf{H}= \frac{\partial^2 E}{\partial \mathbf{w}^2}$是网络输出对权重的 Hessian Matrix，基于网络已经收敛到局部最优的假设，泰勒一阶展开应该比较小，所以忽略第一项。并且由于权重扰动较小，所以也忽略更高阶的展开。我们需要获得最小的$\delta E$

此时对某个权重$\mathbf{w}_q$进行删除的操作表示为

\[ \delta w_q +w_q = 0 \]

将上式用向量$\mathbf{w}$表示

\[ \mathbf{e}_q^T·\delta \mathbf{w} + w_q=0 \]

$\mathbf{e}_q$是权重空间$\mathbf{w}$中对于$w_q$位置的 one-hot 向量

基于以上约束，我们可以使用拉格朗日乘数法来解决该最优化问题

\[ L=\frac{1}{2} \delta \mathbf{w}^T· \mathbf{H}· \delta \mathbf{w} + \lambda(\mathbf{e}_q^T·\delta \mathbf{w}+w_q) \]

可以解得

\[ \delta\mathbf{w}=-\frac{w_q}{[\mathbf{H}^{-1}]_{qq}}\mathbf{H}^{-1}·\mathbf{e}_q \]

\[ L=\frac{1}{2} \frac{w_q^2}{[\mathbf{H}^{-1}]_{qq}} \]

这样我们就得到了一个$\delta\mathbf{w}$使得我们剪切了$w_q$并且调整了其他的权重使得 Loss 的变动最小

有了 OBS 的铺垫，OBQ 很快把这种方式推广到了量化当中，这其实很好理解：常用的量化则是把数值近似到一个接近的值，而剪枝实际上可以看做把数值直接近似成0（某种意义上或许可以称作1bit或0bit量化），可以理解为一种特殊的量化

\[ \mathbf{e}_q^T·\delta \mathbf{w} + w_q= quant(w_q) \]

OBQ 将 OBS 扩展后的公式如下：

\[ \delta\mathbf{w}=-\frac{w_q-quant(w_q)}{[\mathbf{H}_F^{-1}]_{q,q}}(\mathbf{H}_F)^{-1}_{:,q} \]

\[ w_q=\arg \min _q \frac{(quant(w_q)-w_q)^2}{[\mathbf{H}_F^{-1}]_{q,q}} \]

下标$F$代表当前剩余的所有未量化权重，$\mathbf{H}_F$则为对应的 Hessian Matrix

通过不断寻找影响最小的$w_q$进行量化，就能够得到最后的量化模型。在这个过程中我们每量化一个权重$w_q$就要更新当前未量化的权重，并重新计算未量化权重的 Hessian Matrix

GPTQ 算法¶

OBQ 算法在量化结果上表现不错，但是太慢了。OBQ 对 ResNet-50 进行量化需要一个小时，但由于其算法复杂度为$O(d_{row}·d_{col}^3)$，在大模型上将花费几年的时间，所以 GPTQ 方法就是在 OBQ 的基础上进行加速，其改进点总结为以下三点：

取消贪心算法

在 OBQ 中，是逐个找影响最小的 q 来剪枝/量化，经过观察发现，其实随机的顺序效果也一样好（甚至在大模型上更好）。原算法对 W 进行优化时，逐行计算，每一行挑选q的顺序都是不一样的。在 GPTQ 中直接全部都采用固定顺序，使得复杂度从$O(d_{row}·d_{col}^3)$下降到$O(\max (d_{row}·d_{col}^2, d_{col}^3))$。对于一个$d_{raw}=d_{col}=1024$的矩阵来说，复杂度将减少 1000 倍，即 3 个数量级
批处理

OBQ 算法在对单个权重量化完成后，会对所有未量化的权重进行更新来进行补偿。这样的方式是具有较低的 compute-memory-ratio 的，尤其是当未量化的权重比较多的情况。由于同一个特征矩阵 W 不同列间的权重更新是不会互相影响的，GPTQ 提出了批处理的方法，一次处理多个列（例如 128 列）。在一个批次内，仍然是逐列地进行量化，但是暂时不更新批次外的未量化权重，在完成列内的量化后，统一更新未量化的权重，这将大幅提升 compute-memory-ratio

Compute-memory-ratio: 程序执行过程中，FLOPs 计算量与在 global memory 获取的数据量之比，单位为 FLOP/Byte，也称作计算强度
数值稳定性

在 OBQ 计算$\mathbf{H}^{-1}$的方式是利用 Gaussian elimination 迭代计算的，这样能避免求逆的三次复杂度操作

\[ \mathbf{H}^{-1}_{-q} = (\mathbf{H}^{-1}-\frac{1}{[\mathbf{H}^{-1}]_{q,q}}\mathbf{H}^{-1}_{:,q}\mathbf{H}^{-1}_{q,:})_{-q} \]

下标$-q$代表移除矩阵的第$q$行和第$q$列

这个过程会产生数值不稳定的问题，对于小模型可以通过在矩阵对角元素上加一个小量$\lambda$来解决，但对于大模型该方法将仍不奏效。得益于每一行都采用相同的量化顺序，所以他们都共享相同的$\mathbf{H}^{-1}$，GPTQ 采用了提前计算好所有需要的信息，避免该迭代过程。计算这些信息的方法使用的是用 Cholesky decomposition 的形式等价原来的计算结果

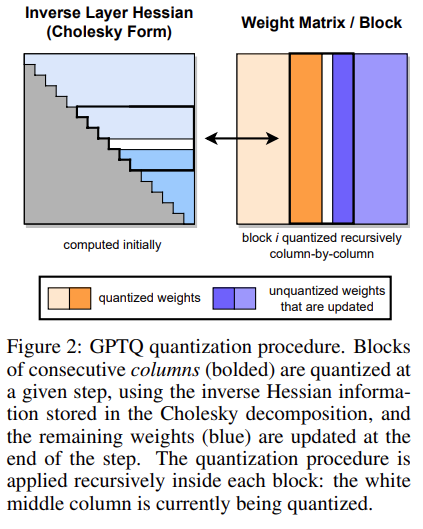
GPTQ 完整的算法图如下

实验结果¶

Quantizing Small Models¶

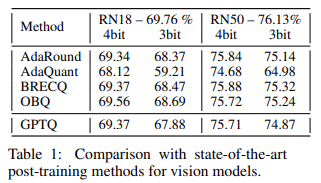
论文测试了 GPTQ 在 ResNet18 & ResNet50 上的量化效果，可以看到在 4-bit 量化中，GPTQ 几乎和最好的方法打平；在 3-bit 量化中略逊色于最好的方法。在量化时间上 GPTQ 只需要 < 1 min 的时间，而 OBQ 方法则需要 1 小时，这是 GPTQ 的优势

Quantizing Big Models¶

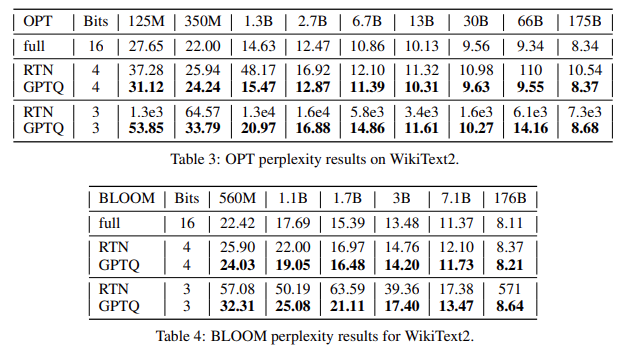
GPTQ 算法在量化 1-3B 参数量的模型只需要几十分钟，对于 175B 参数量的模型则需要 3-4 个小时 (on single A100 GPU)

论文使用 RTN 作为 baseline 进行比较，是全面占优的。在越大的模型上，其量化结果越好

Math in GPTQ¶

Lagrange Multiplier¶

From wiki

the method of Lagrange multipliers is a strategy for finding the local maxima and minima of a function subject to equation constraints

其中函数和约束记为

\[ \displaylines{ f(x_1, x_2, \dots, x_n)\\ g(x_1, x_2, \dots, x_n) = 0 } \]

bilibili 这个视频很好地讲述了拉格朗日乘数法的几何理解：

极值点的必要但不充分条件为：1. 满足约束函数条件；2. 原函数梯度与约束的梯度方向相同

\[ \displaylines{ \begin{cases} \nabla f(x_1, x_2, \dots, x_n) = \lambda \nabla g(x_1, x_2, \dots, x_n) \\ g(x_1, x_2, \dots, x_n) = c \end{cases} } \]

这两个条件可以用一个 lagrange function 并对其变量求偏导来表示

\[ \displaylines{ \mathcal{L}(x_1, x_2, \dots, x_n, \lambda) = f(x_1, x_2, \dots, x_n) - \lambda (g(x_1, x_2, \dots, x_n) - c) \\ \frac{\partial \mathcal{L}}{\partial x_i} = 0 \quad \text{for } i = 1, \dots, n \quad \text{and} \quad \frac{\partial \mathcal{L}}{\partial \lambda} = 0 } \]

利用拉格朗日乘数法就能够轻松推导出 GPTQ 论文中的最优值结论

Schur Complement¶

舒尔补并没有直接在 GPTQ 的论文当中出现，不过在询问各个 ChatGPT 老师的过程中，schur complement 会频繁出现。这里简单列出其形式和重要特性：

对于一个分块矩阵$M$，其中$A$必须是可逆的（如果$D$是可逆的，也可以定义关于$D$的 schur complement）

\[ M = \begin{pmatrix} A & B \\ C & D \end{pmatrix} \]

则矩阵$M$关于块$A$的 schur complement 为

\[ S = D - C A^{-1} B \]

Schur 补最著名的应用是给出分块矩阵$M$的逆的显式表达式（当$A$和$S$均可逆时）

\[ M^{-1} = \begin{pmatrix} A^{-1} + A^{-1} B S^{-1} C A^{-1} & -A^{-1} B S^{-1} \\ -S^{-1} C A^{-1} & S^{-1} \end{pmatrix} \]

为什么重要？ 这个公式将大规模矩阵$M$的求逆问题分解为对较小的子块$A$和$S$的求逆问题，以及一些矩阵乘法。如果$A$和$S$的逆更容易计算（例如，它们是稀疏的、对角化的或已经预先计算好的），这可以显著降低计算复杂度

Inverse of$H_F$¶

在 GPTQ 当中，当我们量化好了某个权重时，就会在 Hessian 矩阵中剔除该权重的位置相关的行和列，然后重新求解子 Hessian 矩阵的逆。在论文当中使用迭代公式求解这个过程

\[ \mathbf{H}^{-1}_{-q} = (\mathbf{H}^{-1}-\frac{1}{[\mathbf{H}^{-1}]_{q,q}}\mathbf{H}^{-1}_{:,q}\mathbf{H}^{-1}_{q,:})_{-q} \]

而这个式子，是不是很像上面提到的 schur complement？但实际上二者的联系并没有看上去那样直接。这个证明过程需要使用到 schur complement

From DeepSeek（不得不感叹现在的 AI 真的很强，直接把整个证明过程写得非常清楚）

将原矩阵进行重新排列

\[ \mathbf{H} = \begin{bmatrix} \mathbf{H}_{-q} & \mathbf{c} \\ \mathbf{d}^\top & e \end{bmatrix} \]

其中：

$\mathbf{H}_{-q}$是移除第$q$行和第$q$列后的$(n-1) \times (n-1)$子矩阵（即我们要求的逆的部分）。

$\mathbf{c}$是$\mathbf{H}$的第$q$列，但移除第$q$行元素（一个$(n-1) \times 1$列向量）。

$\mathbf{d}^\top$是$\mathbf{H}$的第$q$行，但移除第$q$列元素（一个$1 \times (n-1)$行向量）。

$e = \mathbf{H}_{q,q}$是一个标量。

根据 schur complement 的定义，我们可以得到$H^{-1}$的表达式

\[ \mathbf{H}^{-1} = \begin{bmatrix} \mathbf{H}_{-q}^{-1} + \frac{1}{\delta} \mathbf{H}_{-q}^{-1} \mathbf{c} \mathbf{d}^\top \mathbf{H}_{-q}^{-1} & -\frac{1}{\delta} \mathbf{H}_{-q}^{-1} \mathbf{c} \\ -\frac{1}{\delta} \mathbf{d}^\top \mathbf{H}_{-q}^{-1} & \frac{1}{\delta} \end{bmatrix} \]

其中 schur complement$\delta = e - \mathbf{d}^\top \mathbf{H}_{-q}^{-1} \mathbf{c}$

由于我们已经事先求得了$H^{-1}$，所以可以根据上述表达式计算得到$H_{-q}^{-1}$。这其中还需要花费一些功夫，我们把$H^{-1}$也进行分块

\[ \mathbf{H}^{-1} = \begin{bmatrix} \mathbf{A} & \mathbf{m} \\ \mathbf{n}^\top & k \end{bmatrix} \]

从这个分块形式中，我们可以识别：

$\mathbf{H}^{-1}$的右下角元素是$[\mathbf{H}^{-1}]_{q,q} = \frac{1}{\delta}$，因此$\delta = \frac{1}{[\mathbf{H}^{-1}]_{q,q}}$

$\mathbf{H}^{-1}$的第$q$列（移除第$q$行元素，可记为$(\mathbf{H}^{-1}_{:,q})_{-q}$）是$\mathbf{m} = -\frac{1}{\delta} \mathbf{H}_{-q}^{-1} \mathbf{c}$，

$\mathbf{H}^{-1}$的第$q$行（移除第$q$列元素，可记为$(\mathbf{H}^{-1}_{q,:})_{-q}$）是$\mathbf{n}^\top = -\frac{1}{\delta} \mathbf{d}^\top \mathbf{H}_{-q}^{-1}$

我们需要求解$\mathbf{H}_{-q}^{-1}$，其存在于$A$中，我们已知$\mathbf{A} = (\mathbf{H}^{-1})_{-q}$，所以通过一些简单整理就能够得到$\mathbf{H}_{-q}^{-1}$。我们先把$\mathbf{A}$的式子展开：

\[ \mathbf{A} = (\mathbf{H}^{-1})_{-q} = \mathbf{H}_{-q}^{-1} + \frac{1}{\delta} \mathbf{H}_{-q}^{-1} \mathbf{c} \mathbf{d}^\top \mathbf{H}_{-q}^{-1} \]

利用已知的$\mathbf{m}$和$\mathbf{n}^\top$，我们可以计算得到上面的$\mathbf{c}, \mathbf{d}^\top$：

\[ \mathbf{H}_{-q}^{-1} \mathbf{c} = -\delta \mathbf{m}, \quad \mathbf{d}^\top \mathbf{H}_{-q}^{-1} = -\delta \mathbf{n}^\top \]

代入表达式：

\[ (\mathbf{H}^{-1})_{-q} = \mathbf{H}_{-q}^{-1} + \frac{1}{\delta} (-\delta \mathbf{m}) (-\delta \mathbf{n}^\top) = \mathbf{H}_{-q}^{-1} + \delta \mathbf{m} \mathbf{n}^\top \]

得到

\[ \mathbf{H}_{-q}^{-1} = (\mathbf{H}^{-1})_{-q} - \delta \mathbf{m} \mathbf{n}^\top \]

此时所有的量都是已知量，我们把$\mathbf{m}, \mathbf{n}^\top, \delta$，全部换成$\mathbf{H}^{-1}$的表示方式就能得到 GPTQ 中给出的结论了

在此过程中，我们对矩阵$H$进行了重新排布，好消息是排布可以使用相似变换来完成，所以不影响以上证明的最终结论

移动操作的数学本质

将第$q$行/列移动到边界，等价于用排列矩阵$\mathbf{P}$对$\mathbf{H}$做相似变换：

$$
\widetilde{\mathbf{H}} = \mathbf{P} \mathbf{H} \mathbf{P}^\top
$$

其中$\mathbf{P}$是置换矩阵（$\mathbf{P}^{-1} = \mathbf{P}^\top$）。

$\widetilde{\mathbf{H}}$的逆为：

$$
\widetilde{\mathbf{H}}^{-1} = \mathbf{P} \mathbf{H}^{-1} \mathbf{P}^\top
$$

关键点：$\widetilde{\mathbf{H}}$的左上角子矩阵$\widetilde{\mathbf{H}}_{-n}$就是原始$\mathbf{H}_{-q}$（仅行列顺序可能不同，但集合相同）。

Cholesky decomposition¶

From DeepSeek

Cholesky 分解是一种非常重要的矩阵分解方法，专门针对对称正定矩阵。它将一个对称正定矩阵 A 分解为一个下三角矩阵 L 和其转置 Lᵀ 的乘积。

数学表达：
A = L * Lᵀ

其中：

A 是一个 n x n 的 对称正定矩阵。

L 是一个 n x n 的 下三角矩阵（即主对角线以上的元素全为零）。

Lᵀ 是 L 的转置，是一个上三角矩阵。

为什么重要？优势是什么？

高效性： 与通用的 LU 分解相比，Cholesky 分解利用了矩阵的对称正定性，计算量大约只有 LU 分解的一半，并且所需的存储空间也更少（只需要存储 L 矩阵，因为它包含了 Lᵀ 的信息）。这使得它在处理大规模对称正定系统时速度更快、内存占用更低。Cholesky 分解可以通过一种相对直接的算法计算，类似于高斯消元法，但利用了对称性来减少计算量。计算过程逐行/列进行

数值稳定性： 对于对称正定矩阵，Cholesky 分解通常非常数值稳定，不需要进行主元（pivoting）。正定性保证了在计算过程中不会出现除零错误（因为对角线元素 lⱼⱼ 的计算涉及开平方根，而 aⱼⱼ - Σ... 部分保证是正数）。

正定性的检测： 在计算 Cholesky 分解的过程中，如果遇到试图对负数或零开平方根的情况（即 aⱼⱼ - Σ... <= 0），那么就可以立即断定原始矩阵 A 不是正定的。因此，Cholesky 分解算法本身也是一个检查矩阵是否正定的有效方法。

矩阵求逆： 虽然直接求逆通常不推荐（效率低且可能引入数值误差），但如果需要对称正定矩阵 A 的逆，可以通过 Cholesky 分解来实现：

A = L * Lᵀ

A⁻¹ = (Lᵀ)⁻¹ * L⁻¹

求三角矩阵的逆比求一般矩阵的逆高效得多。

Proof of GPTQ correctness¶

在 GPTQ 算法之中直接使用了 Cholesky 分解过后的上三角矩阵$L^T$来替代$\mathbf{H}^{-1}$，在论文当中完全没证明其正确性，关键证明都是一句带过，所以给我带来很大困扰。事实上需要掌握以上的数学工具才能完全理解该过程

要证明 GPTQ 算法的正确性，需要几个额外的关键证明：

证明计算子 Hessian 逆等价于 Cholesky decomposition 子矩阵$L_FL_F^T$

\[ \mathbf{H}^{-1}_{-q} = (\mathbf{H}^{-1}-\frac{1}{[\mathbf{H}^{-1}]_{q,q}}\mathbf{H}^{-1}_{:,q}\mathbf{H}^{-1}_{q,:})_{-q}=L_{F}L_F^T \]

在 GPTQ 的实际使用过程中$q=0$，即永远按照顺序进行量化，我们就证明在$q=0$的情况下，二者是等价的。我们首先对$\mathbf{H}^{-1}$进行分解

\[ \mathbf{H}^{-1} = L L^T = \begin{bmatrix} l_{11} & 0 \\ l_{21} & L_{22} \end{bmatrix} \begin{bmatrix} l_{11} & l_{21}^T \\ 0 & L_{22}^T \end{bmatrix} = \begin{bmatrix} l_{11}^2 & l_{11} l_{21}^T \\ l_{11} l_{21} & l_{21} l_{21}^T + L_{22} L_{22}^T \end{bmatrix}. \]

其中$L_{22}$就是上述提到的$L_{F}$，即剩余的子矩阵，$l_{21}$是一个向量，$l_{11}$是一个标量。根据定义有

1.$[\mathbf{H}^{-1}]_{q,q}=l_{11}^2$
2.$\mathbf{H}^{-1}_{q,:}=[l_{11}, l_{21}]$
3.$\mathbf{H}^{-1}_{:,q}=[l_{11}, l_{21}]^T$

将上述表达式带入到迭代式中既可以求得

\[ \mathbf{H}^{-1}_{-q}== \begin{bmatrix} 0 & 0 \\ 0 & L_{22} L_{22}^T \end{bmatrix}_{-q}=L_{22} L_{22}^T \]
证明使用$L^T$替代$H^{-1}$进行计算是等价的

这个证明过程也不难，因为在第一行二者只相差一个 scale$L_{00}$，这个差异由一个除法进行了消除。具体来说 GPTQ 是为了计算权重的更新量，该式由之前推导得：

\[ \delta\mathbf{w}=-\frac{w_q-quant(w_q)}{[\mathbf{H}^{-1}]_{q,q}}(\mathbf{H})^{-1}_{:,q} \]

由于 GPTQ 是顺序量化，所以这里$q \equiv 0$，易证

\[ \frac{\mathbf{H}^{-1}_{:,0}}{[\mathbf{H}^{-1}]_{0,0}} = \frac{L_{:,0}}{[L]_{0,0}} \]

以上两个证明保证了 GPTQ 算法的正确性：

无需重复计算$\mathbf{H}_F^{-1}$，可以直接使用 Cholesky decomposition 结果
无需使用$\mathbf{H}^{-1}$，可直接使用 Cholesky decomposition 的上三角矩阵作为替代

总结¶

GPTQ 解决了大模型量化的耗时长的问题以及稳定性问题，在 4-bit 要求下能够保持良好的模型精度，并且对于千亿级别的模型，只需要几个小时就能完成量化。在实际使用中，可以先使用 GPTQ 快速地获得一个稳定的基线量化模型，并在此基础上进行精度优化。