cs231n 2021 Assignment 2 note
资源
assignment 模板: github
官方: 课程链接
assignment 参考链接: 2020
发现了一种新的模式: pycharm + git + anaconda & jupyter
上面的组合能够帮助写代码的效率提升,pycharm 能够帮助调试,git 用于版本管理,conda 用于环境管理。jupyter 在测试代码块上有很大的优势,并且很多 cs231n 的作业形式都是以 ipynb 的文件类型发布,更适合在 jupyter 上打开,而且 jupyter 能够直接使用创建好的 conda 环境,特别方便
经过一番折腾,最终决定使用 vs code 替换 pycharm,原因是 vs code 有 jupyter notebook 插件,可以直接显示在 editor 内,比 Pycharm 更方便而且以后想要学习其他语言 vs code 优势更大
过程中的编程复习
重新复习了 numpy 的一些用法,一个重要思想就是尽量少考虑使用循环解决,要以 index 索引思想来解决数据的操作问题。
reshape已经存在的shape
a.reshape(b.shape)当接受参数是元组而是可变参数 args 的时候,可以用 tuple 来将参数变为 *args
np.random.randn(*a.shape)要学会善用矩阵点乘 A * B,是将对应元素相乘,在计算模的时候,或者当其中一个是 indication function 时很有用
重新复习了字典的用法,核心是创造字典,dict(), dict.fromkeys()
字典的 key, val 迭代器,如果不用 items,则只有 key
for key, val in dict.items(): pas对于格式化字符串有新的认知,下面例子
self.params = {} self.params['b%d' % (i+1)] = weight_scale * np.zeros(hd)可以用这样的形式来调用 key
Fully Connected Networks
- 对于网络的认知有了更新。要把层(layer, w)和点(node, x)分开来看,这样网络结构才更清晰。一般隐藏层不包含输出层
- 反向传播熟悉 back propagation,尤其是矩阵相乘的反向传播,只需要记住结论就行了。对于广播过后的结果,需要将广播的矩阵作 sum 处理,得到广播前的对应元素梯度
- 5 layers 和 3 layers 网络优化时比较,差异在哪里?5 layer 更难优化,对于初始值敏感
- 对于优化算法进行了进一步了解,由三个核心点:AdaGrad, Momentum, EWA 最后自然推出 Adam 优化算法
- 在编写代码的时候重要的版本需要保存,这就需要使用 git
Batch normalization
进一步清晰了 bn 的过程与作用,可以回看自己的笔记了解详情
Inline Question 1
How does the scale of weight initialization affect models with/without batch normalization differently, and why?
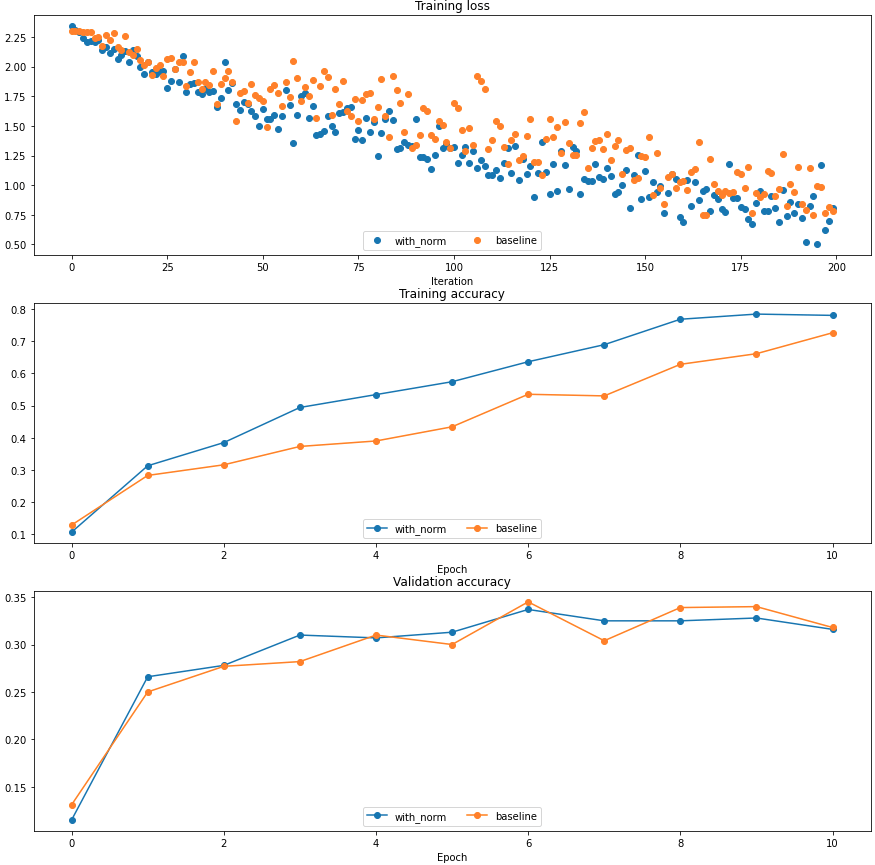
You should find that using batch normalization helps the network to converge much faster.
使用 batch normalization 会让网络在训练集上收敛更快。这和普通的 normalization 是一个道理,减少 zigzag 拐弯
还有几个需要知道和理解的点是:
- batch normalization 帮助缓解梯度消失/爆炸的问题,这将减缓因为 weight initialization 过大或过小而产生梯度消失/爆炸的问题
- batch normalization 有一定的正则化效果,避免过拟合
Inline Question 2
hat does this imply about the relationship between batch normalization and batch size? Why is this relationship observed?
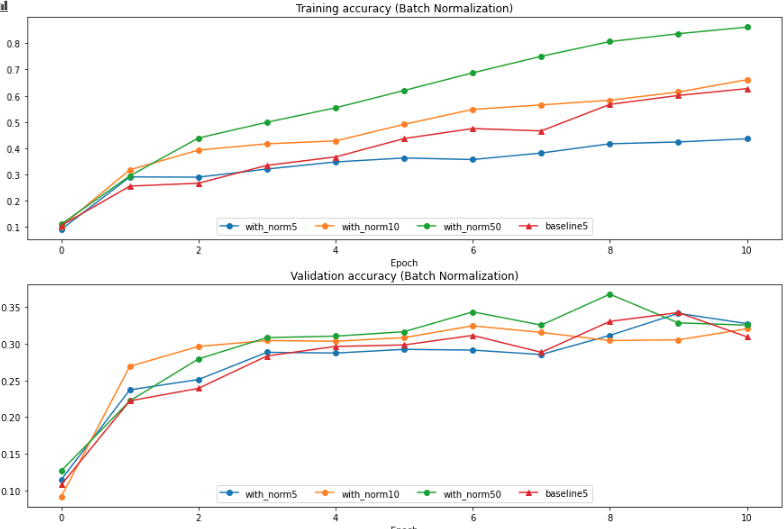
一般规律是:batch size 越大训练集上收敛越快。当 batch size 比较小的时候,比 baseline 速度更慢,原因在于过少的样本带来的偏差太大,这样的噪音会影响训练和测试表现
在训练和测试时均会用到 bn layer,测试时用的 $\mu,\sigma$ 参数是训练过程中的指数加权平均 EWA
Layer Normalization
用在 RNN 中更多,如果以后接触 NLP 领域的话再深入整理。简单的解释 知乎链接
假设我们有 10行 3列 的数据,即我们的batchsize = 10,每一行数据有三个特征,这是一种“列缩放”。
而layer方向相反,它针对的是每一行进行缩放。即只看一笔数据,算出这笔所有特征的均值与方差再缩放。这是一种“行缩放”。
Q: 为什么 gamma 和 beta 还是原来的 (D, ) 形状?Layer normalization 在 RNN 中有什么作用?
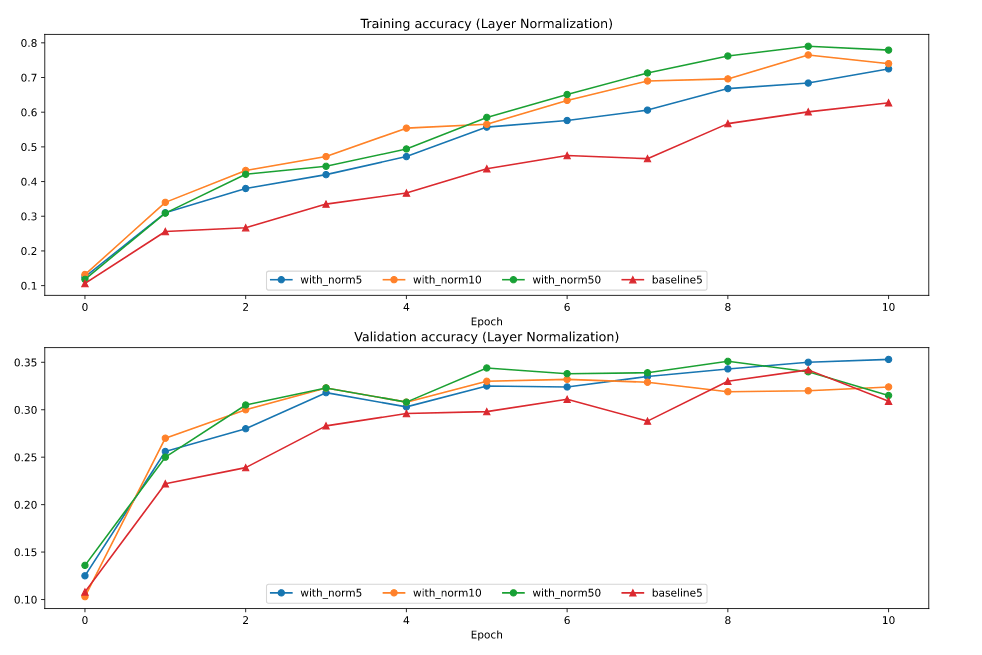
看得出 layer normalization 在训练上也是有一定作用的,但在图像方面相比于 batch normalization 效果差一点,另一个比较自然的结果是,对于 layer normalization 来说 hidden dimension 取较大值较好
Drop out
两行代码解决 (inverted) dropout layer 核心
mask = np.random.rand(*input.shape) < p
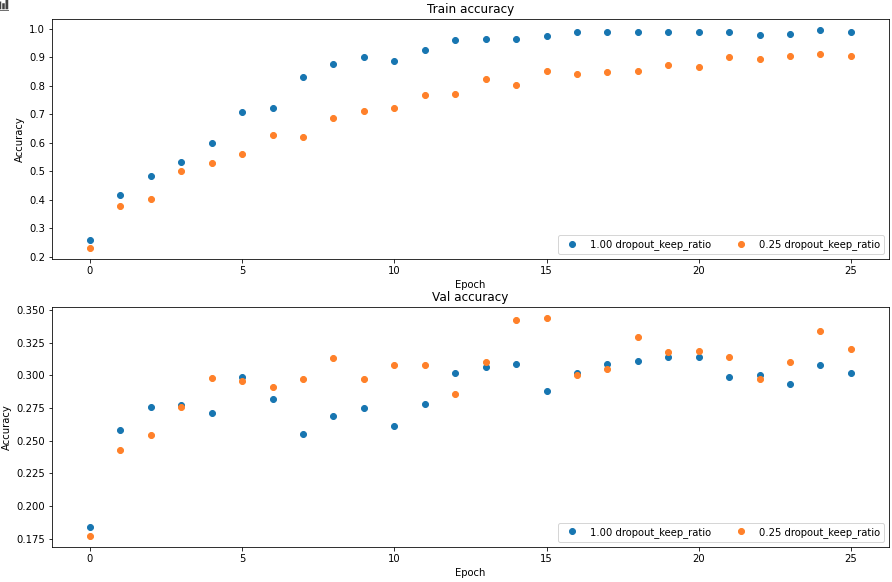
output = input * mask / pvallina dropout 是在 test 时将输出乘以 p 使得输出是一个合理期望值。但如果我们在训练的时候已经除以 p 了,在测试时就不需要作任何操作。下图为正则化效果 regularization
Convolutional Neural Networks
用嵌套循环实现了最原始的卷积操作,使用 np.pad 函数能实现 padding 操作,感觉这个函数的参数不是那么灵活
返回最大值坐标 np.argmax,如果想要返回多元坐标还需要使用 np.unravel_index 转化
np.unravel(indices, shape)assignment 提供了 fast_layers.py 来实现快速卷积操作,比我自己写的循环代码要快 1000 多倍,使用了 im2col 技巧以及 Cpython extension
为什么在正则化的时候正则项中不包括偏差 b? 个人理解认为 b 对于正则化的贡献并不大,而 w 参数则占据了绝大部分的参数。
Spatial Batch Normalization
这是卷积神经网络特有的 batch normalization。之前使用的 batch normalization 面对的是 (N, D) 形状的数据,但卷积过后得到的输出是类似 (N, C, H, W) 这样的多维数据。那我们应该怎样去计算这一批数据的统计量 $\mu, \sigma$ 呢?
如果沿着之前的思维,我们只沿着样本数据轴 N 去计算 $\mu, \sigma$
# data.shape = (N, C, H, W)
mean = np.mean(data, axis=0)
var = np.var(data, axis=0)这将会得到 (C, H, W) 形状的统计量,其中每一个值 (c, h, w),其样本来自于 N 个像素点(同一 channel,同一位置)。但我们希望样本的数量更广泛一些,具体一点来说,我们希望样本来自于 N 个 feature map (H, W),用 numpy 表示为
# data.shape = (N, C, H, W)
mean = np.mean(data, axis=(0, 2, 3))
var = np.var(data, axis=(0, 2, 3))这将会得到 (C,) 形状的统计量,即:得到了对于某一个 channel 的统计量,这是合理的,因为同一个 channel 我们使用的是同一个 kernel。这样我们不仅得到了更广泛样本的统计量,还减少了参数数量
如果要使用之前写的 batch_norm 函数的话可以将数据转化为 (N H W, C) ,在 numpy 中使用 transpose + reshape 就可以完成
data.transpose(0, 2, 3, 1).reshape(-1, C)Spatial Group Normalization
一张图展示Batch Norm, Layer Norm ,Group Norm的区别
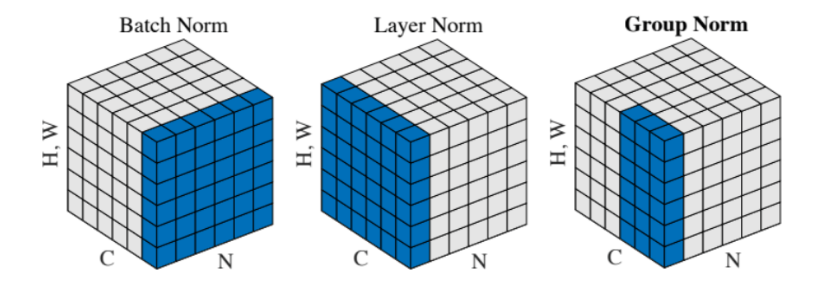
Group Norm可以理解为在layer Norm的基础上,输入维度为 (N, C, H, W),对C进行分组,即 (N, G, C//G, H, W)。为了完成这一部分,重新思考了如何基于系统计算 back propagation
可以以重要的中间变量为节点,根据计算图逐步推导梯度。难点在于有矩阵参与的计算,经常伴随着矩阵形状的改变,在进行 back propagation 中一定要让梯度跟着这些计算进行升维和降维,可以想象为梯度会随着这些节点形状的变化进行复杂的流动,有分流(例如降维度),也有汇合(例如 broadcast)
例如,在 forward pass 中 broadcast 会将矩阵升维,sum 会将矩阵降维,如果在 backward pass 中遇到 broadcast 操作时,则需要将 upper_grad 根据对应维度求和,举个例子,如果我们要求下面 X 的梯度的话,代码应该时这样的
# input: X, X.shape = (N, D)
# f(X) = X - np.mean(X)
# upper_grad = dout, dout.shape = (N, D)
dmean = np.sum(dout, axis=0) # sum broadcast dimension
dmean = dmean / N # mean operation back prop
dX = dout - dmean如果想不使用计算图直接按照一般的矩阵梯度计算,遇到对矩阵/向量求导时,就会出现张量,也就是说维度会增加,需要熟悉张量的运算及其思维。还是借用上面的例子,但我们把平均值作为 (N, D) 形状来看待
# input: X, X.shape = (N, D)
# f(X) = X - np.mean(X) * np.ones(X.shape)
# upper_grad = dout, dout.shape = (N, D)这将是一种普适的方法,更加抽象化,能够处理任何的矩阵求导,但不推荐实际中使用。
不论使用哪种方法,最核心的还是要理解梯度流动的本质——某一个变量的变动能够引起输出多少变动
BUG
Fully Connected Layer
现在卡在了 solver 上
不能得到 overfitting 的结果
尝试更换 solver 看能否得到不一样的结果
失败了
尝试使用2016的所有答案,看是否是自己的代码出问题了
失败了
小技巧 Ctrl+r 能够更换 pycharm 相同字段
尝试更改 colab 本身的文件,使用2016年的colab文件
成功,原因在于 learning rate 太小了,不能找到全局最优
Batch normalization
卡在了计算 back prop 上
最后出现的失误还是在于每一个公式必须要精确才行
norm_x = (x - sample_mean) / np.sqrt(sample_var + eps) norm_x = (x - sample_mean) / (np.sqrt(sample_var) + eps)上面两个式子虽然在计算结果上相差不多,但是在网络的计算中,一点点的误差传播过后会变得越来越大
尝试使用 jupyter 进行编程,遇到问题:The kernel appears to have died. It will restart automatically
以为是 jupyter 的问题,但测试了不同的软件都出错了,最终发现是自己代码的问题!当找了一圈没有找到答案时,可能就要怀疑自己了,而不是怀疑软件出了问题!不过这也有好处,让我决定放弃使用 pycharm 转战 vs code