D2L 06 卷积神经网络

本章介绍的卷积神经网络（convolutional neural network，CNN）是一类强大的、为处理图像数据而设计的神经网络。 基于卷积神经网络结构的模型在计算机视觉领域中已经占主导地位，当今几乎所有的图像识别、对象检测或语义分割相关的学术竞赛和商业应用都以这种方法为基础

从全连接层到卷积

MLP 的需要将数据展开到一维，这将带来大量的参数开销，以及忽略数据之间的结构信息。CNN 是机器学习利用自然图像中一些已知结构的创造性方法

为了让网络能够适合于计算机视觉，需要有两个特征：

1. 平移不变性：对相同的图像区域具有相似的反应
2. 局部性：只探索输入图像中的局部区域，而不过度在意图像中相隔较远区域的关系

教材用了几个公式的转变来完成这两个特征

1. 全连接层公式表达，$H,U,W\ or \ V,X$ 分别表示输出（隐藏层），偏置，权重，输入。下标表示图形长宽

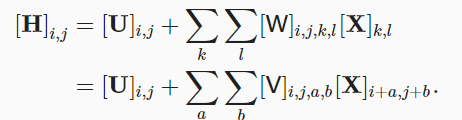
1. 加入平移不变性

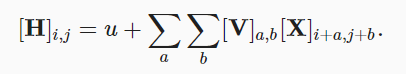
1. 加入局部性

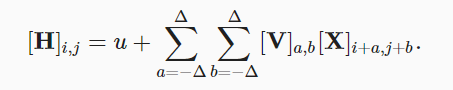
​ 上面就是一个基本的卷积层，$V$ 为卷积核（convolution kernel）或者滤波器（filter）

1. 加入通道

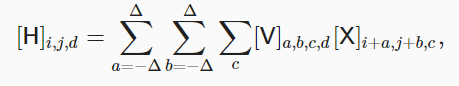
教材还介绍了一下数学上的卷积操作，与我们实际使用的卷积操作是不一样的，图像卷积操作在数学上叫做互相关（cross-correlation），该操作是卷积的“未翻转”版本。为了与深度学习文献中的标准术语保持一致，我们将继续把“互相关运算”称为卷积运算

图像卷积

互相关/卷积运算图解

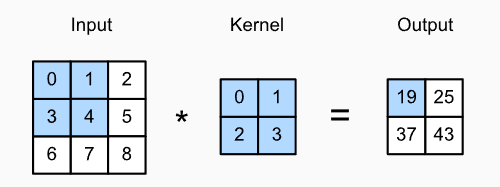
注意，输出大小略小于输入大小。这是因为卷积核的宽度和高度大于1， 而卷积核只与图像中每个大小完全适合的位置进行互相关运算。下面简单实现一个自己的卷积层

import torch
from torch import nn


def corr2d(X, K):  #@save
    """计算二维互相关运算。"""
    h, w = K.shape
    Y = torch.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1))
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            Y[i, j] = (X[i:i + h, j:j + w] * K).sum()
    return Y

class Conv2D(nn.Module):
    def __init__(self, kernel_size):
        super().__init__()
        self.weight = nn.Parameter(torch.rand(kernel_size))
        self.bias = nn.Parameter(torch.zeros(1))

    def forward(self, x):
        return corr2d(x, self.weight) + self.bias

学习卷积核

教材举了一个例子：能够用一个 [1, -1] 的简单卷积核来检测横向边缘。但是不可能所有卷积核是人工构造的，好消息是我们可以像之前的 MLP 一样使用优化算法估计出一个卷积核来达到期望的效果。最终通过梯度下降法学习到的权重为 [0.9895, -0.9873] 与人工设计卷积核十分接近

实际上可能存在各种各样的卷积核，这些卷积核能够提取不同的特征，例如：图像边缘，服饰膨胀，二阶求导等。如果要去人工设计这么多功能的卷积核，就回到了传统计算机视觉，另一个选择就是设计一个网络，然后使用优化算法去学习，但是学习到的卷积核可解释性就不强了

特征映射和感受野

教材说到：卷积层有时被称为特征映射（Feature Map）。由于 Map 的意义在英文里有多个，也可以被翻译为地图，Feature Map 也常被翻译为特征图谱，而教材应该就是想表述为“映射”，以表示 CNN 对于特征的提取作用

填充和步幅

填充和步幅可用于有效地调整数据的维度

填充

在应用多层卷积时，我们常常丢失边缘像素。在许多情况下，我们需要设置 $p_h=k_h−1$ 和 $p_w=k_w−1$ 去填充（padding）图像周围，使输入和输出具有相同的高度和宽度。如果 kernel size 为奇数就能在左右上下均匀得填充了

步幅

有时候为了高效计算或是缩减采样次数，卷积窗口可以跳过中间位置，每次滑动多个元素。我们将每次滑动元素的数量称为步幅（stride）

多输入多输出通道

多输入通道

当输入包含多个通道时，需要构造一个与输入数据具有相同输入通道数目的卷积核，以便与输入数据进行互相关运算。我们演示了一个具有两个输入通道的二维互相关运算的示例

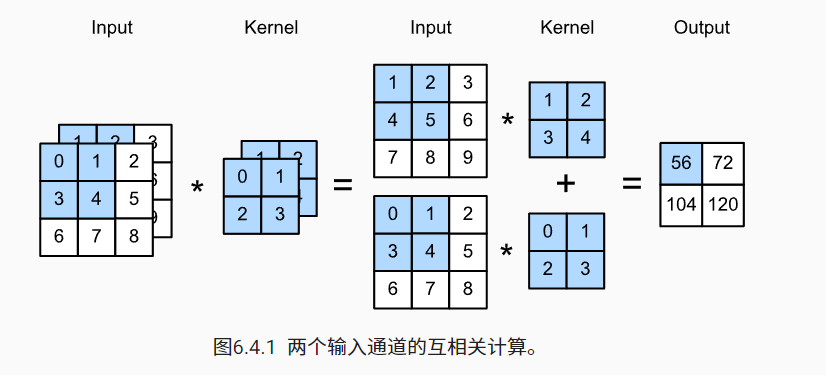
多输出通道

每一层有多个输出通道是至关重要的。在最流行的神经网络架构中，随着神经网络层数的加深，我们常会增加输出通道的维数，通过减少空间分辨率以获得更大的通道深度。直观地说，我们可以将每个通道看作是对不同特征的响应

1x1 卷积层

1x1 卷积看起来似乎没有多大意义。 毕竟，卷积的本质是有效提取相邻像素间的相关特征，但是这样的操作实际上非常常见

我们可以将 1x1 卷积层看作是在每个像素位置应用的全连接层。这里输入和输出具有相同的高度和宽度，输出中的每个元素都是从输入图像中同一位置的元素的线性组合

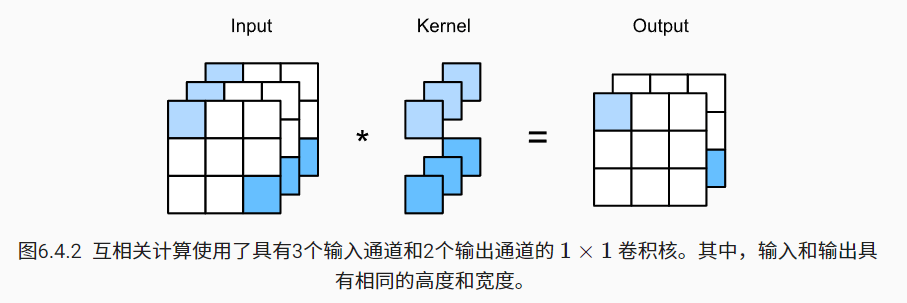
注意：在后面的图示和代码当中，很少能看到 bias 出现，但实际上如果没有特殊指定，默认都是存在 bias，其数量与卷积核数量相同

汇聚层

也通常叫做池化层（pooling layer），它通常具有两个目的：

1. 降低卷积层对位置的敏感性
2. 对输出进行降采样

对于“敏感性”的说法，我觉得不太好理解，在吴恩达的视频里提到：池化层能提高所提取特征的鲁棒性。这让我联想到了自己看的 PointNet：使用了 maxpooling 来将所有点的特征提取为 global 特征，我认为这里有着相似的作用。因为 maxpooling 是一个对称函数，对于一些位置的变换（噪声）其输出是不会有改变的。我们将窗口中最大的数作为整个窗口的“代表”，忽略其他较小的值，以整体把握

最大池化和平均池化

与卷积层类似，汇聚层运算符由一个固定形状的窗口组成，该窗口根据其步幅大小在输入的所有区域上滑动。在池化窗口到达的每个位置，它计算该窗口中输入子张量的最大值或平均值

在处理多通道输入数据时，汇聚层在每个输入通道上单独运算，而不是像卷积层一样在通道上对输入进行汇总

胡思乱想😅

是否可以直接通过卷积操作替代池化层？因为卷积也能够降低图谱的分辨率，显然平均池化是可以被替代的，但最大池化呢？看到一个 知乎 链接 [卷积神经网络中的pooling层能否用相同stride的convolution层替代]) 有所讨论，其中有人评论：max pooling 是动态的，而 strided convolution 是静态的，二者不可一概而论

现在正在证明一件事：可以使用神经网络实现最大值分类/回归问题，下面介绍一下我的实验结果：

1. 实验数据为1000个数对，从 (0， 20000) 中进行采样
2. ReLU 需要输入大多数为正数，负数太多梯度会迅速消失，当然数据的归一化也有很不错的效果
3. 通过一个简单网络，我可以很好的训练出一个最大最小值分类模型，但是对于回归模型仍然需要更多努力
4. 显然原始数据对于最大值回归问题是很重要的，或许对于其他的回归问题也很重要。如果得到了最大最小值的分类，只需要将分类结果与原始数据相乘即可得到最大值。按照这个思路我也得到期望的结果，但是学习率非常非常小大概到了 1e-8 次方级别，最终损失在 5 左右
5. 即使不使用“相乘”操作，实际上我也能人工构造出一个网络，得到不错的结果，按照我的想法，网络没办法通过优化算法获得我所设计的参数，但是这个问题很快在更宽更多的网络层下被解决，实际的 loss 在 0.05 左右，我认为这是一个相当不错的结果
6. 使用 SGD 无法得到优化结果，只能使用 Adam，对于稀疏数据/模型可能需要自适应的学习率，可以先用 Adam 快速收敛再用 SGD 调整
7. 使用 mini-batch 无法得到优化结果，batch size 只能等于一，batch size 越大越容易搜索到 sharp minimum，参考 知乎

根据以上实验，我认为 strided convolution 具有替代 max pooling 的能力，另一些笼统的感受是：

1. 分类任务想比回归任务更加简单
2. 可能对于有高精度的（回归）任务深度学习是需要一定辅助的，但在大量复杂数据的情景下，深度学习相比人类具有无法比拟的优势
3. 一开始认为需要使用原始数据进行回归，尝试了 ResNet，但实际上并不需要，普通的全连接层即可完成

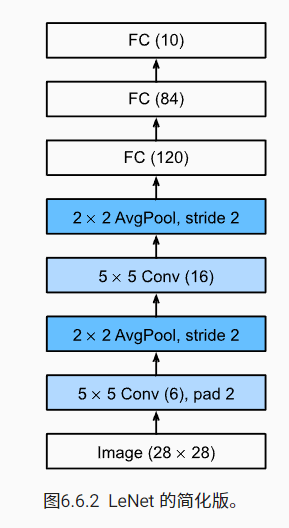
LeNet

当时， LeNet 取得了与支持向量机（support vector machines）性能相媲美的成果，成为监督学习的主流方法。直接上图和代码就能够清楚其结构

import torch
from torch import nn


class Reshape(nn.Module):
    def forward(self, x):
        return x.view(-1, 1, 28, 28)

net = torch.nn.Sequential(
    Reshape(),
    nn.Conv2d(1, 6, kernel_size=5, padding=2), nn.Sigmoid(),
    nn.AvgPool2d(kernel_size=2, stride=2),
    nn.Conv2d(6, 16, kernel_size=5), nn.Sigmoid(),
    nn.AvgPool2d(kernel_size=2, stride=2),
    nn.Flatten(),
    nn.Linear(16 * 5 * 5, 120), nn.Sigmoid(),
    nn.Linear(120, 84), nn.Sigmoid(),
    nn.Linear(84, 10))

为了凸显简单，教材直接使用一个 nn.Sequential 将所有的模块连接起来，并请注意，虽然 ReLU 和最大汇聚层更有效，但它们在20世纪90年代还没有出现