D2L 07 现代卷积神经网络
虽然深度神经网络的概念非常简单——将神经网络堆叠在一起。但由于不同的网络结构和超参数选择,这些神经网络的性能会发生很大变化。 本章介绍的神经网络是将人类直觉和相关数学见解结合后,经过大量研究试错后的结晶。 我们会按时间顺序介绍这些模型,在追寻历史的脉络的同时,帮助你培养对该领域发展的直觉。这将有助于你研究开发自己的结构。 例如,本章介绍的批量归一化(batch normalization)和残差网络(ResNet)为设计和训练深度神经网络提供了重要思想指导
一点历史
在传统机器学习方法中,计算机视觉流水线是由经过人的手工精心设计的特征流水线组成的(SIFT, SURF, HOG)。将提取的特征放到最喜欢的分类器中(例如线性模型或其它核方法),以训练分类器
对于这些传统方法,大部分的进展都来自于对特征有了更聪明的想法,并且学习到的算法往往归于事后的解释
机器学习是一个正在蓬勃发展、严谨且非常有用的领域。然而,如果你和计算机视觉研究人员交谈,他们会告诉你图像识别的诡异事实——推动领域进步的是数据特征,而不是学习算法。计算机视觉研究人员相信,从对最终模型精度的影响来说,更大或更干净的数据集、或是稍微改进的特征提取,比任何学习算法带来的进步要大得多
一组研究人员,包括 Yann LeCun, Geoff Hinton, Yoshua Bengio, Andrew Ng, Shun ichi Amari 和 Juergen Schmidhuber,他们认为特征本身应该被学习
深度卷积神经网络的突破出现在2012年。突破可归因于两个关键因素:
- 数据:包含许多特征的深度模型需要大量的有标签数据,才能显著优于基于凸优化的传统方法
- GPU:并行计算以及高内存带宽实现快速卷积运算
AlexNet
2012年,AlexNet 横空出世。它首次证明了学习到的特征可以超越手工设计的特征。AlexNet 使用了8层卷积神经网络,并以很大的优势赢得了2012年 ImageNet (224x224) 图像识别挑战赛
有趣的是,在网络的最底层,AlexNet 学习到了一些类似于传统滤波器的特征抽取器。AlexNet 的更高层建立在这些底层表示的基础上,以表示更大的特征
尽管一直有一群执着的研究者不断钻研,试图学习视觉数据的逐级表征,然而很长一段时间里这些尝试都未有突破
AlexNet & LeNet
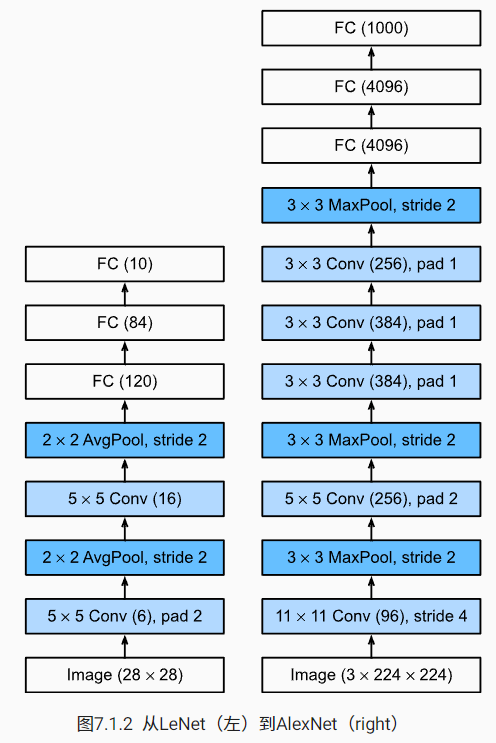
AlexNet和LeNet的设计理念非常相似,但也存在一些差异,除了层数更深,通道更多,其他关键的改变还有:
- 激活函数从 sigmoid 改为 ReLU
- 使用了 dropout 正则化
- 使用了数据增强
下面看看模型的代码
import torch
from torch import nn
net = nn.Sequential(
# 这里,我们使用一个11*11的更大窗口来捕捉对象。
# 同时,步幅为4,以减少输出的高度和宽度。
# 另外,输出通道的数目远大于LeNet
nn.Conv2d(1, 96, kernel_size=11, stride=4, padding=1), nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2),
# 减小卷积窗口,使用填充为2来使得输入与输出的高和宽一致,且增大输出通道数
nn.Conv2d(96, 256, kernel_size=5, padding=2), nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2),
# 使用三个连续的卷积层和较小的卷积窗口。
# 除了最后的卷积层,输出通道的数量进一步增加。
# 在前两个卷积层之后,汇聚层不用于减少输入的高度和宽度
nn.Conv2d(256, 384, kernel_size=3, padding=1), nn.ReLU(),
nn.Conv2d(384, 384, kernel_size=3, padding=1), nn.ReLU(),
nn.Conv2d(384, 256, kernel_size=3, padding=1), nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2),
nn.Flatten(),
# 这里,全连接层的输出数量是LeNet中的好几倍。使用dropout层来减轻过度拟合
nn.Linear(6400, 4096), nn.ReLU(),
nn.Dropout(p=0.5),
nn.Linear(4096, 4096), nn.ReLU(),
nn.Dropout(p=0.5),
# 最后是输出层。由于这里使用Fashion-MNIST,所以用类别数为10,而非论文中的1000
nn.Linear(4096, 10))今天,AlexNet已经被更有效的结构所超越,但它是从浅层网络到深层网络的关键一步。尽管AlexNet的代码只比LeNet多出几行,但学术界花了很多年才接受深度学习这一概念,并应用其出色的实验结果
VGG
VGG 让网络的结构更加模块化,下面我们定义一个 vgg_block 来实现一个组合:Convolution + Activation + Pooling
import torch
from torch import nn
def vgg_block(num_convs, in_channels, out_channels):
layers = []
for _ in range(num_convs):
layers.append(nn.Conv2d(in_channels, out_channels,
kernel_size=3, padding=1))
layers.append(nn.ReLU())
in_channels = out_channels
layers.append(nn.MaxPool2d(kernel_size=2,stride=2))
return nn.Sequential(*layers)利用定义好的模块和各种超参数,搭建 VGG 网络
# 定义 (num_conv, out_channels)
conv_arch = ((1, 64), (1, 128), (2, 256), (2, 512), (2, 512))
def vgg(conv_arch):
conv_blks = []
in_channels = 1
# 卷积层部分
for (num_convs, out_channels) in conv_arch:
conv_blks.append(vgg_block(num_convs, in_channels, out_channels))
in_channels = out_channels
return nn.Sequential(
*conv_blks, nn.Flatten(),
# 全连接层部分
nn.Linear(out_channels * 7 * 7, 4096), nn.ReLU(), nn.Dropout(0.5),
nn.Linear(4096, 4096), nn.ReLU(), nn.Dropout(0.5),
nn.Linear(4096, 10))
net = vgg(conv_arch)在 VGG 论文中,Simonyan 和 Ziserman 尝试了各种架构。特别是他们发现深层且窄的卷积(即3×3)比较浅层且宽的卷积更有效
NiN
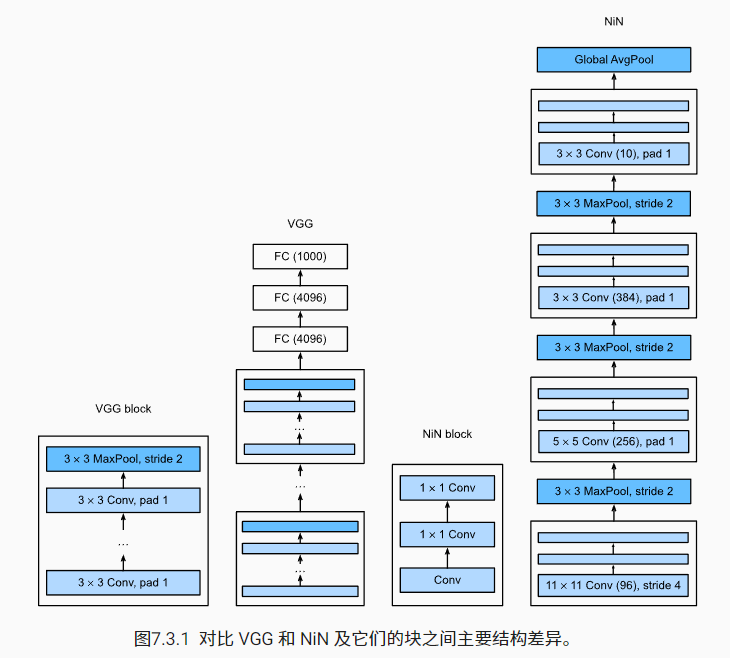
全连接层的输入和输出通常是分别对应于样本和特征的二维张量,这个参数数量相比卷积核是非常大的,NiN 和 AlexNet 之间的一个显著区别是 NiN 完全取消了全连接层。NiN 的想法是在每个像素位置(针对每个高度和宽度)应用一个 1x1 的卷积(可视为像素级全连接层)以替代全连接层,下面直接上图示和代码
import torch
from torch import nn
def nin_block(in_channels, out_channels, kernel_size, strides, padding):
return nn.Sequential(
nn.Conv2d(in_channels, out_channels, kernel_size, strides, padding),
nn.ReLU(),
nn.Conv2d(out_channels, out_channels, kernel_size=1), nn.ReLU(),
nn.Conv2d(out_channels, out_channels, kernel_size=1), nn.ReLU())
net = nn.Sequential(
nin_block(1, 96, kernel_size=11, strides=4, padding=0),
nn.MaxPool2d(3, stride=2),
nin_block(96, 256, kernel_size=5, strides=1, padding=2),
nn.MaxPool2d(3, stride=2),
nin_block(256, 384, kernel_size=3, strides=1, padding=1),
nn.MaxPool2d(3, stride=2),
nn.Dropout(0.5),
# 标签类别数是10
nin_block(384, 10, kernel_size=3, strides=1, padding=1),
# 最后放一个 全局平均汇聚层(global average pooling layer),生成一个多元逻辑向量(logits)
# 将四维的输出转成二维的输出,其形状为(批量大小, 10)
nn.AdaptiveAvgPool2d((1, 1)),
nn.Flatten())NiN 设计的优点是,它显著减少了模型所需参数的数量,这也减少了过拟合。然而,在实践中,这种设计有时会增加训练模型的时间
GoogLeNet
在 GoogLeNet 中,基本的卷积块被称为 Inception 块(Inception block)论文的一个观点是,有时使用不同大小的卷积核组合是有利的。其中 Google 中的 L 为大写,以致敬 LeNet
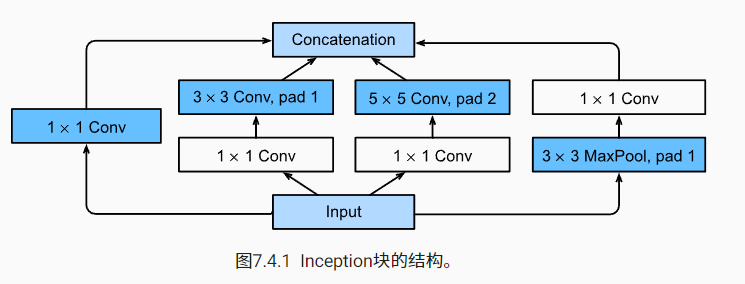
这四条路径都使用合适的填充来使输入与输出的高和宽一致,最后我们将每条线路的输出在通道维度上连结,并构成 Inception 块的输出。在 Inception 块中,通常调整的超参数是每层输出通道的数量(很难调,这也是 GoogLeNet 难以复现的原因之一)。下面是 Inception 块的代码
import torch
from torch import nn
from torch.nn import functional as F
class Inception(nn.Module):
# `c1`--`c4` 是每条路径的输出通道数
def __init__(self, in_channels, c1, c2, c3, c4, **kwargs):
super(Inception, self).__init__(**kwargs)
# 线路1,单1 x 1卷积层
self.p1_1 = nn.Conv2d(in_channels, c1, kernel_size=1)
# 线路2,1 x 1卷积层后接3 x 3卷积层
self.p2_1 = nn.Conv2d(in_channels, c2[0], kernel_size=1)
self.p2_2 = nn.Conv2d(c2[0], c2[1], kernel_size=3, padding=1)
# 线路3,1 x 1卷积层后接5 x 5卷积层
self.p3_1 = nn.Conv2d(in_channels, c3[0], kernel_size=1)
self.p3_2 = nn.Conv2d(c3[0], c3[1], kernel_size=5, padding=2)
# 线路4,3 x 3最大汇聚层后接1 x 1卷积层
self.p4_1 = nn.MaxPool2d(kernel_size=3, stride=1, padding=1)
self.p4_2 = nn.Conv2d(in_channels, c4, kernel_size=1)
def forward(self, x):
p1 = F.relu(self.p1_1(x))
p2 = F.relu(self.p2_2(F.relu(self.p2_1(x))))
p3 = F.relu(self.p3_2(F.relu(self.p3_1(x))))
p4 = F.relu(self.p4_2(self.p4_1(x)))
# 在通道维度上连结输出
return torch.cat((p1, p2, p3, p4), dim=1)整个模型图示
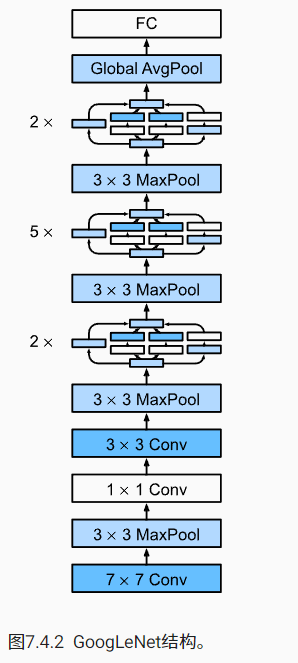
Inception 块之间的最大汇聚层可降低维度,1x1 卷积块的作用之一就是维度转换,这样可以通过减少通道数降低网络参数
Batch Normalization
这是一种流行且有效的技术,可持续加速深层网络的收敛速度,直观形式是:控制每一层的输出分布。现在具体来看批量归一化(batch normalization)的形式,用 $x∈\mathcal B$ 表示一个来自小批量的输入
应用标准化后,生成的小批量的平均值为0和单位方差为1,$\gamma, \beta$ 是需要学习的参数,通常被认为是拉伸参数和偏移参数,$\epsilon$ 为一个小量以确保不除以零
批量归一化层
批量归一化是一种线性变换,通常作用在输出和激活函数之间,对于全连接层和卷积层的批量归一化略有不同(BatchNorm1d->BatchNorm2d)
批量归一化也可以看作一种正则化技术,它在训练和测试阶段的表现是不一样的。通常在预测阶段,通过移动平均估算整个训练数据集的样本均值和方差,并在预测时使用它们以替代训练过程中的小批量均值和方差
代码实现
教材给出了一个从零实现版本
import torch
from torch import nn
def batch_norm(X, gamma, beta, moving_mean, moving_var, eps, momentum):
# 通过 `is_grad_enabled` 来判断当前模式是训练模式还是预测模式
if not torch.is_grad_enabled():
# 如果是在预测模式下,直接使用传入的移动平均所得的均值和方差
X_hat = (X - moving_mean) / torch.sqrt(moving_var + eps)
else:
assert len(X.shape) in (2, 4)
if len(X.shape) == 2:
# 使用全连接层的情况,计算特征维上的均值和方差
mean = X.mean(dim=0)
var = ((X - mean) ** 2).mean(dim=0)
else:
# 使用二维卷积层的情况,计算通道维上(axis=1)的均值和方差。
# 这里我们需要保持X的形状以便后面可以做广播运算
mean = X.mean(dim=(0, 2, 3), keepdim=True)
var = ((X - mean) ** 2).mean(dim=(0, 2, 3), keepdim=True)
# 训练模式下,用当前的均值和方差做标准化
X_hat = (X - mean) / torch.sqrt(var + eps)
# 更新移动平均的均值和方差
moving_mean = momentum * moving_mean + (1.0 - momentum) * mean
moving_var = momentum * moving_var + (1.0 - momentum) * var
Y = gamma * X_hat + beta # 缩放和移位
return Y, moving_mean.data, moving_var.data上面仅实现了核心功能,如果要结合到 pytorch 模块中还需要用 Module 类来包装一下,这里就不记录了。直接使用 pytorch 的 API 只需要指定输入的 channel 数即可,下面是在原始的 LeNet 上使用 batch normalization 的代码
net = nn.Sequential(
nn.Conv2d(1, 6, kernel_size=5), nn.BatchNorm2d(6), nn.Sigmoid(),
nn.MaxPool2d(kernel_size=2, stride=2),
nn.Conv2d(6, 16, kernel_size=5), nn.BatchNorm2d(16), nn.Sigmoid(),
nn.MaxPool2d(kernel_size=2, stride=2), nn.Flatten(),
nn.Linear(256, 120), nn.BatchNorm1d(120), nn.Sigmoid(),
nn.Linear(120, 84), nn.BatchNorm1d(84), nn.Sigmoid(),
nn.Linear(84, 10))批量归一化做了什么
- 固定小批量中的均值和方差,维护数值的相对稳定,能加速收敛,减缓了梯度消失/爆炸的情况,但一般不改变模型精度
- 固定小批量中的均值和方差,引入了噪声,起到了正则化的作用。这是一个意想不到的“副作用”
实际上对于批量归一化的原理并没有一个明确的答案,原论文提到的“减少内部协变量偏移”的动机似乎不是一个有效的解释。如果非要给这个问题给出自己的胡乱理解,我认为是控制输出分布能够让数值更稳定,在一个统一标准下的空间超平面的分割分会更好,或许这种数值稳定对于梯度爆炸和梯度消失也有一定作用
ResNet
加深网络一定能提升模型的表现吗?答案不是肯定的,下面这张图形象地展示原因
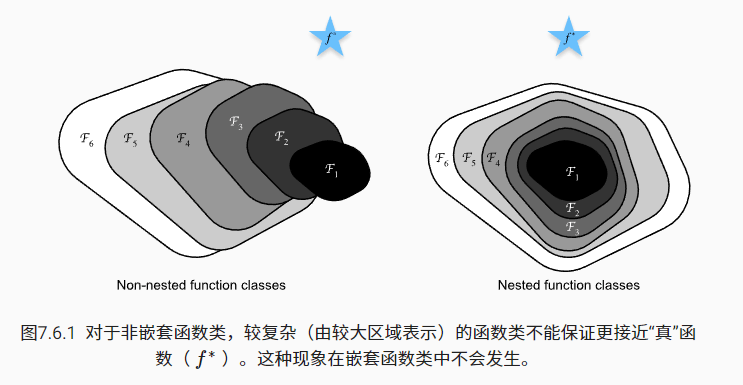
只有当较复杂的函数类包含较小的函数类时,我们才能确保增大搜索范围时,搜索得到的结果能更接近最优解。对于深度神经网络,如果我们能将新添加的层训练成恒等映射(identity function)$f(x)=x$,新模型和原模型将同样有效
针对这一问题,何恺明等人提出了残差网络(ResNet),它在2015年的 ImageNet 图像识别挑战赛夺魁,并深刻影响了后来的深度神经网络的设计
残差块
假设我们的原始输入为 $x$ ,而希望学出的理想映射为 $f(x)$,普通的块和残差块的表现形式如下
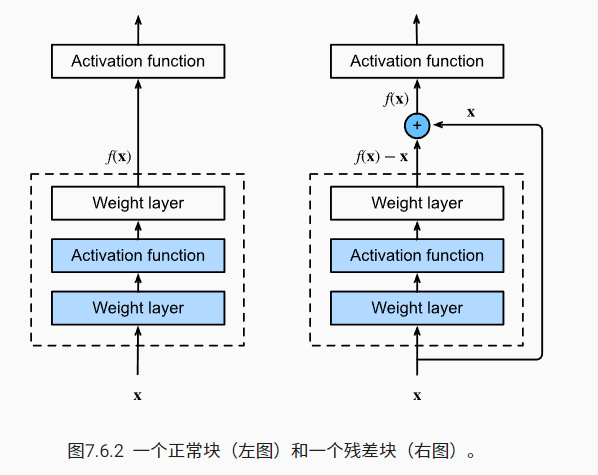
重点关注右侧的结构,在该结构下,虚线框内所学到的映射将是一个残差 $g(x) = f(x) - x$(假设我们能够学到理想映射),所以取名为残差块。这样的模块将很容易学习恒等变换,只需要将所有的权重置零即可
为了让输出和输入能够相加,显然要求输入和输出是具有相同形状和相同通道数,这个问题可以使用 1x1 卷积层解决。ResNet 中的残差块图示如下
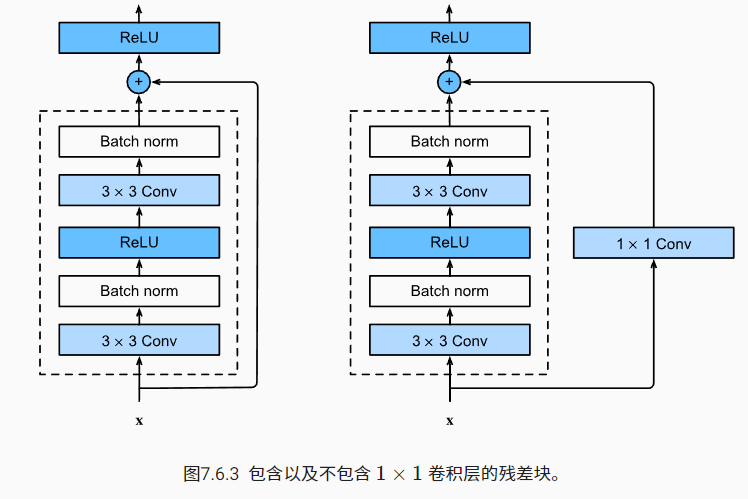
代码将更清晰地展示其中的细节
import torch
from torch import nn
from torch.nn import functional as F
class Residual(nn.Module): #@save
def __init__(self, input_channels, num_channels,
use_1x1conv=False, strides=1):
super().__init__()
self.conv1 = nn.Conv2d(input_channels, num_channels,
kernel_size=3, padding=1, stride=strides)
self.conv2 = nn.Conv2d(num_channels, num_channels,
kernel_size=3, padding=1)
if use_1x1conv:
self.conv3 = nn.Conv2d(input_channels, num_channels,
kernel_size=1, stride=strides)
else:
self.conv3 = None
self.bn1 = nn.BatchNorm2d(num_channels)
self.bn2 = nn.BatchNorm2d(num_channels)
self.relu = nn.ReLU(inplace=True)
def forward(self, X):
Y = F.relu(self.bn1(self.conv1(X)))
Y = self.bn2(self.conv2(Y))
if self.conv3:
X = self.conv3(X)
Y += X
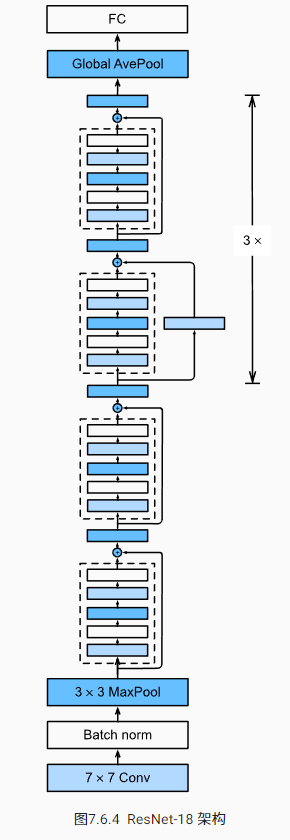
return F.relu(Y)ResNet 模型
ResNet 的前两层跟之前介绍的 GoogLeNet 中的一样,不同之处在于 ResNet 每个卷积层后增加了批量归一化层
b1 = nn.Sequential(nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),
nn.BatchNorm2d(64), nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2, padding=1))GoogLeNet 在后面接了 4 个由Inception块组成的模块。 ResNet 则使用 4 个由残差块组成的模块,每个模块使用若干个同样输出通道数的残差块,定义由残差块组成的 resnet_block
def resnet_block(input_channels, num_channels, num_residuals,
first_block=False):
blk = []
for i in range(num_residuals):
# 对第一个模块做特别处理,不需要对维度进行转换
if i == 0 and not first_block:
blk.append(Residual(input_channels, num_channels,
use_1x1conv=True, strides=2))
else:
blk.append(Residual(num_channels, num_channels))
return blk现在在 ResNet 中加入所有残差块,这里每个模块使用 2 个残差块
b2 = nn.Sequential(*resnet_block(64, 64, 2, first_block=True))
b3 = nn.Sequential(*resnet_block(64, 128, 2))
b4 = nn.Sequential(*resnet_block(128, 256, 2))
b5 = nn.Sequential(*resnet_block(256, 512, 2))最后,与 GoogLeNet 一样,在 ResNet 中加入全局平均汇聚层,以及全连接层输出
net = nn.Sequential(b1, b2, b3, b4, b5,
nn.AdaptiveAvgPool2d((1,1)),
nn.Flatten(), nn.Linear(512, 10))每个模块有 4 个卷积层(不包括恒等映射的 1×1 卷积层)。 加上第一个 7×7 卷积层和最后一个全连接层,共有 18 层。 因此,这种模型通常被称为 ResNet-18。虽然 ResNet 的主体结构跟 GoogLeNet类似,但 ResNet 结构更简单,修改也更方便。这些因素都导致了 ResNet 迅速被广泛使用