D2L 09 现代循环神经网络

循环神经网络在实践中一个常见问题是数值不稳定性。 尽管我们已经应用了梯度裁剪等技巧来缓解这个问题， 但是仍需要通过设计更复杂的序列模型可以进一步处理它。 具体来说，我们将引入两个广泛使用的网络， 即门控循环单元（gated recurrent units，GRU）和 长短期记忆网络（long short-term memory，LSTM）。 然后，我们将基于一个单向隐藏层来扩展循环神经网络架构。 我们将描述具有多个隐藏层的深层架构， 并讨论基于前向和后向循环计算的双向设计。 现代循环网络经常采用这种扩展

事实上，语言建模只揭示了序列学习能力的冰山一角。 在各种序列学习问题中，如自动语音识别、文本到语音转换和机器翻译， 输入和输出都是任意长度的序列。 为了阐述如何拟合这种类型的数据， 我们将以机器翻译为例介绍基于循环神经网络的 “编码器－解码器”架构和束搜索，并用它们来生成序列

由于我对于 RNN 的研究甚少，所以这些章节整理将会比较粗糙

门控循环单元（GRU）

对于一个系列来说，不是每一个观察值都是同等重要，我们希望循环神经网络能够记住想要的观察，忽略不重要观察。GRU 使用了两个门：更新门和重置门来达到这样的目的，两个门具有以下两个显著特征：

• 重置门有助于捕获序列中的短期依赖关系
• 更新门有助于捕获序列中的长期依赖关系

这意味着模型有专门的机制来确定应该何时更新隐状态， 以及应该何时重置隐状态。 这些机制是可学习的，并且能够解决了上面列出的问题。 例如，如果第一个词元非常重要， 模型将学会在第一次观测之后不更新隐状态。 同样，模型也可以学会跳过不相关的临时观测

门控隐状态

重置门和更新门

先看一个简单图解

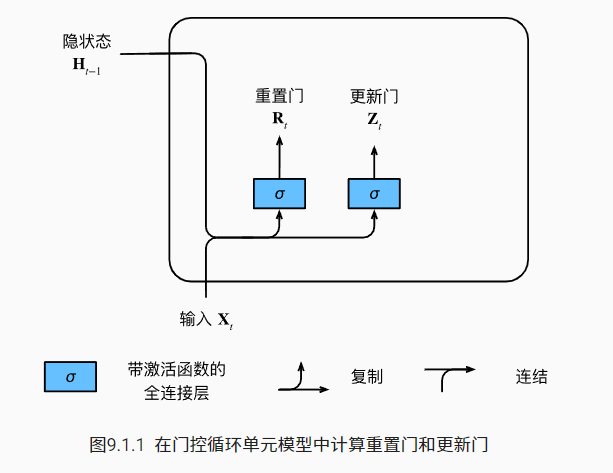
再来看其数学表达，对于给定的时间步 t，假设输入是一个小批量 $X_t∈R^{n×d}$， 上一个时间步的隐状态是 $H_{t−1}∈R^{n×h}$ ，重置门 $R_t∈R^{n×h}$和更新门 $Z_t∈R^{n×h}$

$$\begin{aligned} \mathbf{R}_{t} &=\sigma\left(\mathbf{X}_{t} \mathbf{W}_{x r}+\mathbf{H}_{t-1} \mathbf{W}_{h r}+\mathbf{b}_{r}\right), \\ \mathbf{Z}_{t} &=\sigma\left(\mathbf{X}_{t} \mathbf{W}_{x z}+\mathbf{H}_{t-1} \mathbf{W}_{h z}+\mathbf{b}_{z}\right), \end{aligned}$$

使用 sigmoid 函数将输入值转换到区间 (0,1)，权重将 $X_t$ 和 $H_{t-1}$ 转化到维度为 $h$ 的隐状态

候选隐状态

将重置门 $R_t$ 与常规隐状态更新机制集成， 得到在时间步 t 的候选隐状态（candidate hidden state） $\tilde{H}_t \in R^{n \times h}$

$$\tilde{\mathbf{H}}_{t}=\tanh \left(\mathbf{X}_{t} \mathbf{W}_{x h}+\left(\mathbf{R}_{t} \odot \mathbf{H}_{t-1}\right) \mathbf{W}_{h h}+\mathbf{b}_{h}\right)$$

符号 ⊙ 是 Hadamard 积（按元素乘积）运算符，我们使用 tanh 非线性激活函数来确保候选隐状态中的值保持在区间 (−1,1) 中

当重置门接近为1就回到普通的循环神经网络，若重置门为0则放弃之前的隐状态

隐状态

更新门将 $H_{t-1}$ 和 $\tilde{H}_t$ 之间进行按元素的凸组合，以确定保留多少上一步的隐状态，到此就得出了门控循环单元的最终更新公式

$$\mathbf{H}_{t}=\mathbf{Z}_{t} \odot \mathbf{H}_{t-1}+\left(1-\mathbf{Z}_{t}\right) \odot \tilde{\mathbf{H}}_{t}$$

最后放一个“花哨”的图示，来表示整个流程，实际上并没有数学表达看起来清晰

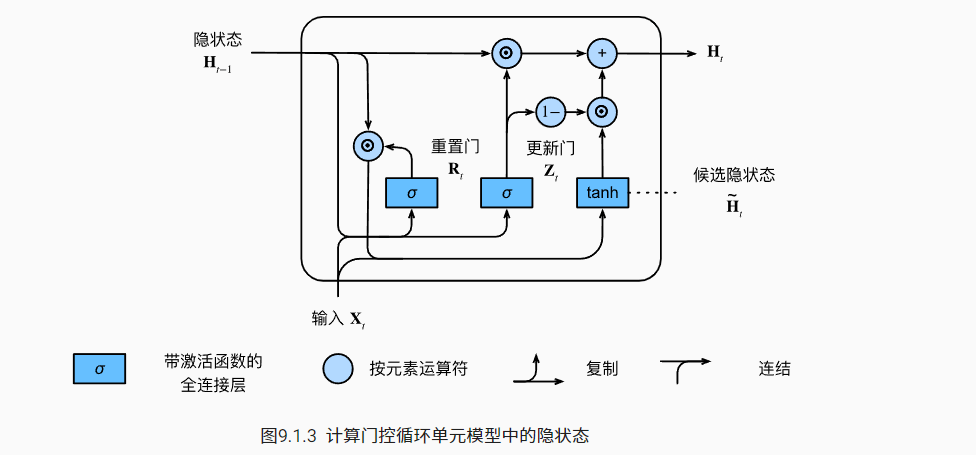
到现在我都挺难以理解这两个门的作用，只能自己生硬理解了：

1. 重置门，决定当前候选隐状态对于当前输入的影响程度（及时），能够让网络更轻松地关注当下
2. 更新门，有点像残差一样，决定保留多少前一时刻隐状态的特征（长期），能够让网络更轻松地记住之前

实现

以上四个公式就是 GRU 的核心，贴一下从零实现的 GRU 核心代码，略去数据的初始化和隐状态的初始化

def gru(inputs, state, params):
    W_xz, W_hz, b_z, W_xr, W_hr, b_r, W_xh, W_hh, b_h, W_hq, b_q = params
    H, = state
    outputs = []
    for X in inputs:
        Z = torch.sigmoid((X @ W_xz) + (H @ W_hz) + b_z)
        R = torch.sigmoid((X @ W_xr) + (H @ W_hr) + b_r)
        H_tilda = torch.tanh((X @ W_xh) + ((R * H) @ W_hh) + b_h)
        H = Z * H + (1 - Z) * H_tilda
        Y = H @ W_hq + b_q
        outputs.append(Y)
    return torch.cat(outputs, dim=0), (H,)

简洁实现 GRU 只需要一行，将其替换上一节的 RNN 单元，即可得到新的 RNN 模型

num_inputs = vocab_size
gru_layer = nn.GRU(num_inputs, num_hiddens)
model = d2l.RNNModel(gru_layer, len(vocab))
model = model.to(device)
d2l.train_ch8(model, train_iter, vocab, lr, num_epochs, device)

长短期记忆网络（LSTM）

长期以来，隐变量模型存在着长期信息保存和短期输入缺失的问题。 解决这一问题的最早方法之一是长短期存储器（long short-term memory，LSTM），有趣的是，长短期记忆网络的设计比门控循环单元稍微复杂一些， 却比门控循环单元早诞生了近20年

门控记忆元

该记忆元的实现比 GRU 稍微复杂一点，下面具体来看看

输入门、遗忘门和输出门

同样先看一个简单图解

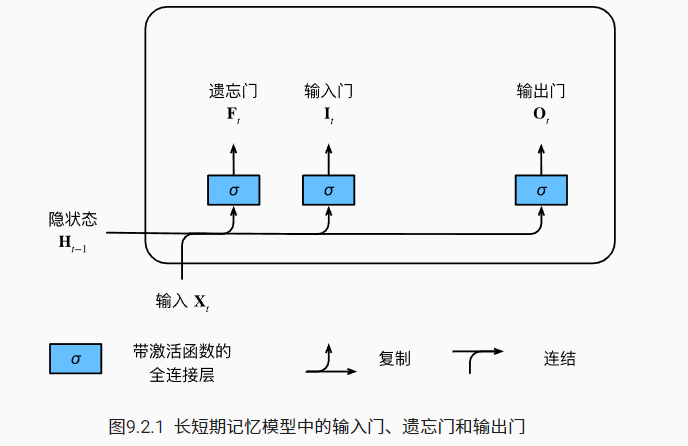
再来看其数学表达式

$$\begin{aligned} \mathbf{I}_{t} &=\sigma\left(\mathbf{X}_{t} \mathbf{W}_{x i}+\mathbf{H}_{t-1} \mathbf{W}_{h i}+\mathbf{b}_{i}\right) \\ \mathbf{F}_{t} &=\sigma\left(\mathbf{X}_{t} \mathbf{W}_{x f}+\mathbf{H}_{t-1} \mathbf{W}_{h f}+\mathbf{b}_{f}\right) \\ \mathbf{O}_{t} &=\sigma\left(\mathbf{X}_{t} \mathbf{W}_{x o}+\mathbf{H}_{t-1} \mathbf{W}_{h o}+\mathbf{b}_{o}\right) \end{aligned}$$

就是和 GRU 的更新门和重置门一样的公式

候选记忆元

类似于 GRU 的候选隐状态，也是受用 tanh 作为激活函数，但是不同的是没有其他门控的参与

$$\tilde{\mathbf{C}}_{t}=\tanh \left(\mathbf{X}_{t} \mathbf{W}_{x c}+\mathbf{H}_{t-1} \mathbf{W}_{h c}+\mathbf{b}_{c}\right)$$

记忆元

现在基础的材料准备完毕，开始进行组合控制。类似于 GRU 的最后隐状态更新，但是使用的是记忆元和两个门，其表达式如下

$$\mathbf{C}_{t}=\mathbf{F}_{t} \odot \mathbf{C}_{t-1}+\mathbf{I}_{t} \odot \tilde{\mathbf{C}}_{t}$$

隐状态

最终的隐状态更新公式为

$$\mathbf{H}_{t}=\mathbf{O}_{t} \odot \tanh \left(\mathbf{C}_{t}\right)$$

实现

从零实现的核心代码如下，同样这里忽略数据初始化和隐状态初始化

def lstm(inputs, state, params):
    [W_xi, W_hi, b_i, W_xf, W_hf, b_f, W_xo, W_ho, b_o, W_xc, W_hc, b_c,
     W_hq, b_q] = params
    (H, C) = state
    outputs = []
    for X in inputs:
        I = torch.sigmoid((X @ W_xi) + (H @ W_hi) + b_i)
        F = torch.sigmoid((X @ W_xf) + (H @ W_hf) + b_f)
        O = torch.sigmoid((X @ W_xo) + (H @ W_ho) + b_o)
        C_tilda = torch.tanh((X @ W_xc) + (H @ W_hc) + b_c)
        C = F * C + I * C_tilda
        H = O * torch.tanh(C)
        Y = (H @ W_hq) + b_q
        outputs.append(Y)
    return torch.cat(outputs, dim=0), (H, C)

看可以看到 LSTM 除了隐状态 $H_t$ 需要传递到下一个时间步，还需要传递记忆元 $C_t$，简洁实现如下

num_inputs = vocab_size
lstm_layer = nn.LSTM(num_inputs, num_hiddens)
model = d2l.RNNModel(lstm_layer, len(vocab))
model = model.to(device)
d2l.train_ch8(model, train_iter, vocab, lr, num_epochs, device)

教材仅仅是简单介绍了这些结构，对于这些结构为什么有用并没有深入分析。在吴恩达讲解的 GRU 讲解了一个简化版本，即没有重置门的版本，这就让重置门的作用变得更加模糊了。以我愚蠢的见解来看，GRU 的两个门控作用可能来自以下直觉：

1. 以残差网络的观点来理解更新门，能够让网络更好学习恒等变换，即方便保留历史信息
2. 重置门进一步增加网络灵活性，对隐状态加以权重，是否放弃历史状态以专注当前输入

深度循环神经网路

到目前为止，我们只讨论了具有一个单向隐藏层的循环神经网络， 而在循环神经网络中，我们首先需要确定如何添加更多的层， 以及在哪里添加额外的非线性

下面描述了一个具有 L 个隐藏层的深度循环神经网络， 每个隐状态都连续地传递到当前层的下一个时间步和下一层的当前时间步

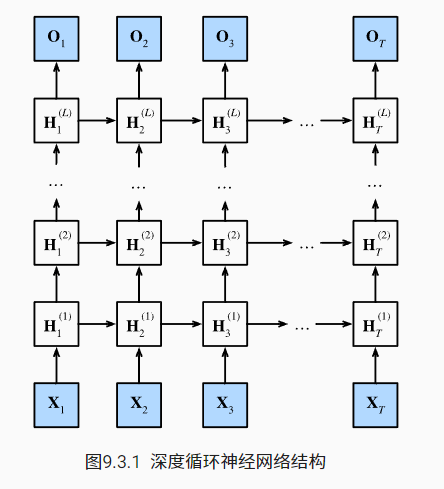
数学表示如下：

$$\mathbf{H}_{t}^{(l)}=\phi_{l}\left(\mathbf{H}_{t}^{(l-1)} \mathbf{W}_{x h}^{(l)}+\mathbf{H}_{t-1}^{(l)} \mathbf{W}_{h h}^{(l)}+\mathbf{b}_{h}^{(l)}\right)\\ \mathbf{O}_{t}=\mathbf{H}_{t}^{(L)} \mathbf{W}_{h q}+\mathbf{b}_{q}$$

与多层感知机一样，隐藏层数目 L 和隐藏单元数目 h 都是超参数

简介实现

只需要多加一个参数 num_layers 就可以搞定了

vocab_size, num_hiddens, num_layers = len(vocab), 256, 2
num_inputs = vocab_size
device = d2l.try_gpu()
lstm_layer = nn.LSTM(num_inputs, num_hiddens, num_layers)
model = d2l.RNNModel(lstm_layer, len(vocab))
model = model.to(device)

由于使用了长短期记忆网络模型来实例化两个层，因此训练速度被大大降低了（左侧为单层 GRU，右侧为两层 GRU）

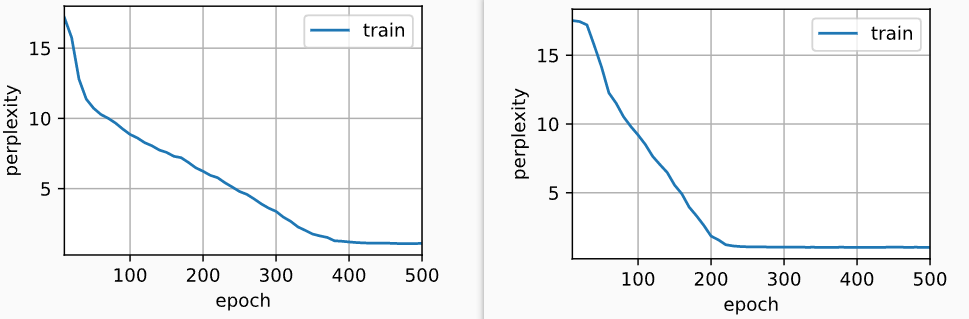
双向循环神经网络

双向循环神经网络的一个关键特性是：使用来自序列两端的信息来估计输出。 也就是说，我们使用来自过去和未来的观测信息来预测当前的观测。 但是在对下一个词元进行预测的情况中，这样的模型并不是我们所需的

双向层的使用在实践中非常少，并且仅仅应用于部分场合。 例如，填充缺失的单词、词元注释（例如，用于命名实体识别） 以及作为序列处理流水线中的一个步骤对序列进行编码（例如，用于机器翻译）

$$\begin{array}{l} \overrightarrow{\mathbf{H}}_{t}=\phi\left(\mathbf{X}_{t} \mathbf{W}_{x h}^{(f)}+\overrightarrow{\mathbf{H}}_{t-1} \mathbf{W}_{h h}^{(f)}+\mathbf{b}_{h}^{(f)}\right) \\ \overleftarrow{\mathbf{H}}_{t}=\phi\left(\mathbf{X}_{t} \mathbf{W}_{x h}^{(b)}+\overleftarrow{\mathbf{H}}_{t+1} \mathbf{W}_{h h}^{(b)}+\mathbf{b}_{h}^{(b)}\right) \end{array}$$

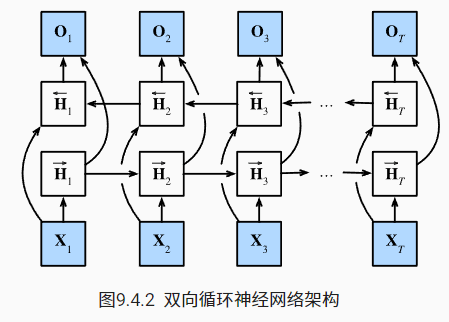
将两个方向的隐状态连接起来进行对输出的预测

$$\mathbf{O}_{t}=\mathbf{H}_{t} \mathbf{W}_{h q}+\mathbf{b}_{q}$$

机器翻译与数据集

需要了解的点：

1. 机器翻译的数据集是由源语言和目标语言的文本序列对组成的

2. 在机器翻译中，我们更喜欢单词级词元化 （最先进的模型可能使用更高级的词元化技术）其中每个词元要么是一个词，要么是一个标点符号

3. 由于机器翻译数据集由语言对组成， 因此我们可以分别为源语言和目标语言构建两个词表

4. 我们还指定了额外的特定词元， 例如在小批量时用于将序列填充到相同长度的填充词元（“”）， 以及序列的开始词元（“”）和结束词元（“”）。 这些特殊词元在自然语言处理任务中比较常用

5. 在机器翻译中，每个样本都是由源和目标组成的文本序列对， 其中的每个文本序列可能具有不同的长度。为了提高计算效率，我们仍然可以通过截断（truncation）和 填充（padding）方式实现一次只处理一个小批量的文本序列

编码器-解码器架构

为了处理这种类型的输入和输出， 我们可以设计一个包含两个主要组件的架构： 第一个组件是一个编码器（encoder）： 它接受一个长度可变的序列作为输入， 并将其转换为具有固定形状的编码状态。 第二个组件是解码器（decoder）： 它将固定形状的编码状态映射到长度可变的序列。 这被称为编码器-解码器（encoder-decoder）架构

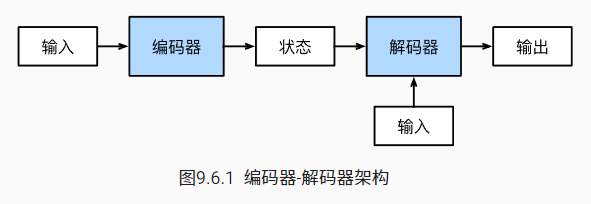
序列到序列学习（seq2seq）

本节，我们将使用两个循环神经网络的编码器和解码器， 并将其应用于序列到序列（sequence to sequence，seq2seq）类的学习任务

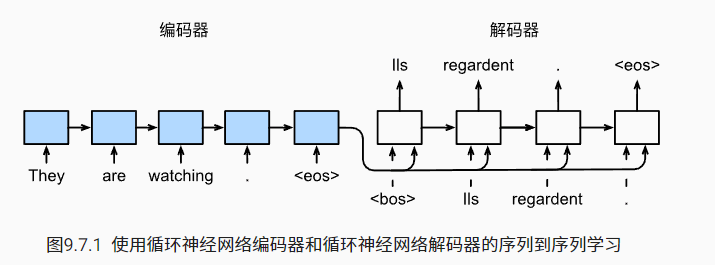
循环神经网络编码器使用长度可变的序列作为输入， 将其转换为固定形状的隐状态。 为了连续生成输出序列的词元， 独立的循环神经网络解码器是基于输入序列的编码信息和输出序列已经看见的（train mode）或者生成的词元（test mode）来预测下一个词元

需要了解的点：

1. 图示结构中，编码器最终的隐状态在每一个时间步都作为解码器的输入序列的一部分。具体来说是和 input 进行维度连接 torch.cat

2. 编码器 RNN 是没有输出层的，并且可以是双向 RNN

3. 在训练时解码器使用标签作为输入；推理时解码器使用上一时间步的输出作为输入

4. 衡量生成序列的好坏使用 BLEU (bilingual evaluation understudy)

   $$\exp \left(\min \left(0,1-\frac{\text { len }_{\text {label }}}{\text { len }_{\text {pred }}}\right)\right) \prod_{n=1}^{k} p_{n}^{1 / 2^{n}}$$

   关于 BLEU:

   1. BLEU 值越大表示结果越好

   2. 其中 len 表示词元数，k 是用于匹配的最长的 n 元语法。 另外，用 $p_n$ 表示 n 元语法的精确度，它是两个数量的比值：

      $$\frac{\text{matched n-gram number}}{\text{total predicted n-gram number}}$$

      第一个是预测序列与标签序列中匹配的 n 元语法的数量， 第二个是预测序列中 n 元语法的数量。看个小例子，来自教材的讲解视频 bilibili

      

   3. n-gram 语法中，n 越大对其越重视（BLEU 中指数的原因）

看看编码器和解码器的代码

#@save
class Seq2SeqEncoder(d2l.Encoder):
    """用于序列到序列学习的循环神经网络编码器"""
    def __init__(self, vocab_size, embed_size, num_hiddens, num_layers,
                 dropout=0, **kwargs):
        super(Seq2SeqEncoder, self).__init__(**kwargs)
        # 嵌入层
        self.embedding = nn.Embedding(vocab_size, embed_size)
        self.rnn = nn.GRU(embed_size, num_hiddens, num_layers,
                          dropout=dropout)

    def forward(self, X, *args):
        # 输出'X'的形状：(batch_size,num_steps,embed_size)
        X = self.embedding(X)
        # 在循环神经网络模型中，第一个轴对应于时间步
        X = X.permute(1, 0, 2)
        # 如果未提及状态，则默认为0
        output, state = self.rnn(X)
        # output的形状:(num_steps,batch_size,num_hiddens)
        # state[0]的形状:(num_layers,batch_size,num_hiddens)
        return output, state

class Seq2SeqDecoder(d2l.Decoder):
    """用于序列到序列学习的循环神经网络解码器"""
    def __init__(self, vocab_size, embed_size, num_hiddens, num_layers,
                 dropout=0, **kwargs):
        super(Seq2SeqDecoder, self).__init__(**kwargs)
        self.embedding = nn.Embedding(vocab_size, embed_size)
        self.rnn = nn.GRU(embed_size + num_hiddens, num_hiddens, num_layers,
                          dropout=dropout)
        self.dense = nn.Linear(num_hiddens, vocab_size)

    def init_state(self, enc_outputs, *args):
        return enc_outputs[1]

    def forward(self, X, state):
        # 输出'X'的形状：(batch_size,num_steps,embed_size)
        X = self.embedding(X).permute(1, 0, 2)
        # 广播context，使其具有与X相同的num_steps
        context = state[-1].repeat(X.shape[0], 1, 1)
        X_and_context = torch.cat((X, context), 2)
        output, state = self.rnn(X_and_context, state)
        output = self.dense(output).permute(1, 0, 2)
        # output的形状:(batch_size,num_steps,vocab_size)
        # state[0]的形状:(num_layers,batch_size,num_hiddens)
        return output, state

束搜索（beam search）

贪心搜索

对于输出序列的每一时间步 t′， 我们都将基于贪心搜索从输出中找到具有最高条件概率的词元

$$y_{t^{\prime}}=\underset{y \in \mathcal{Y}}{\operatorname{argmax}} P\left(y \mid y_{1}, \ldots, y_{t^{\prime}-1}, \mathbf{c}\right)$$

那么贪心搜索存在的问题是什么呢？ 现实中，最优序列（optimal sequence）应该是最大化

$$\prod_{t^{\prime}=1}^{T^{\prime}} P\left(y_{t^{\prime}} \mid y_{1}, \ldots, y_{t^{\prime}-1}, \mathbf{c}\right)$$

这是基于输入序列生成输出序列的条件概率。 然而，贪心搜索无法保证得到最优序列

穷举搜索

虽然穷举搜索能保证最优解，但其计算量是不可接受的，为 $O(|Y|^{T’})$ 其中 Y 为词表长度，T’ 为输出最大长度

束搜索

束搜索（beam search）是贪心搜索的一个改进版本。 它有一个超参数，名为束宽（beam size）k。 在时间步1，我们选择具有最高条件概率的 k 个词元。 在随后的每个时间步，基于上一时间步的 k 个候选输出序列， 我们将继续从 k|Y| 个可能的选择中挑出具有最高条件概率的 k 个候选输出序列，图示如下

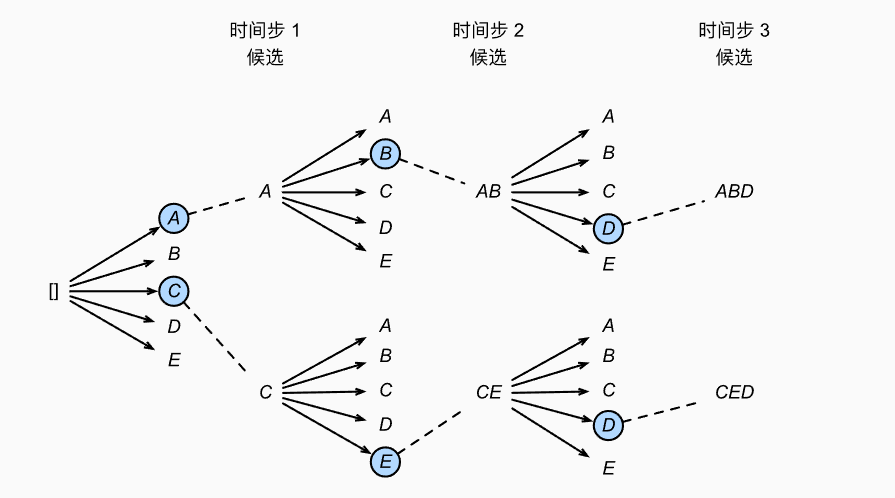
束搜索的计算量为 $O(k|Y|T’)$

对于我们获得最终候选输出序列集合（不仅仅是最后 k 个集合，还可以包含之前的候选系列），选择其中条件概率乘积最高的序列作为输出序列

$$\frac{1}{L^{\alpha}} \log P\left(y_{1}, \ldots, y_{L} \mid \mathbf{c}\right)=\frac{1}{L^{\alpha}} \sum_{t^{\prime}=1}^{L} \log P\left(y_{t^{\prime}} \mid y_{1}, \ldots, y_{t^{\prime}-1}, \mathbf{c}\right)$$

其中 L 部分是对长句的奖励，就像 BLEU 一样