D2L 10 注意力机制

555终于可以开始看注意力机制了😆Transformer 我来啦！

注意力提示

生物学中的注意力提示

主要有两个概念：

1. 非自主性提示/非随意线索（non-volitional cue），基于环境中物体的突出性和易见性
2. 自主性提示/随意线索（volitional cue），受主观意愿推动

查询、键和值

教材对于这三个概念的解释并不清晰，还是看沐神的讲解吧 bilibili

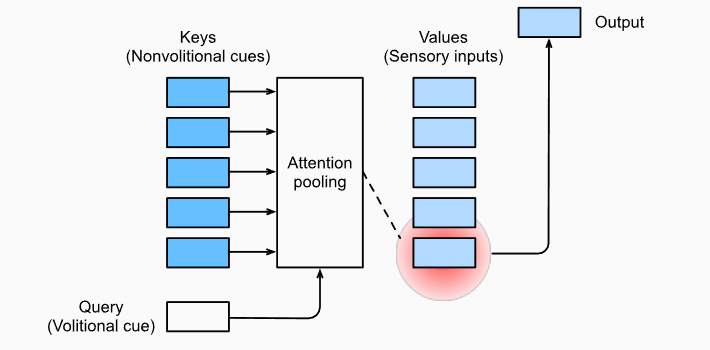
卷积、全连接、池化层都只考虑不随意线索，注意力机制则显式地考虑随意线索：

1. 随意线索被称之为查询（query）
2. 每个输入是一个键值对 (key, value)，其中 key 可视为非随意线索，（下面这句是我自己乱想的）value 可以视为该线索的相关属性
3. 通过注意力池化层来有偏向性的选择某些输入

非参数注意力汇聚：Nadaraya-Watson 核回归

实际上一个数学表达的例子能够更清楚展示这三个概念。给定数据 $(x_i, y_i), i=1,…,n$

给定查询 $x$，平均池化将获得输出

$$f(x) = \frac{1}{n}\sum_{i}{y_i}$$

这就是没有注意力机制的情况，与查询值无关，全凭非随意线索获得输出。而更好的方案是60年代提出来的 Nadaraya-Waston 核回归

$$f(x)=\sum_{i=1}^{n} \frac{K\left(x-x_{i}\right)}{\sum_{j=1}^{n} K\left(x-x_{j}\right)} y_{i}$$

其中 K 可以看作一个核函数，例如一个高斯核，用于衡量两点之间的距离

$$K(u)=\frac{1}{\sqrt{2 \pi}} \exp \left(-\frac{u^{2}}{2}\right)$$

这就将注意力机制显式地用于输出，也就是给各个 value 加入相关权重。现在再来看这个图示可能会更好

带参数注意力汇聚

非参数的Nadaraya-Watson核回归具有一致性（consistency）的优点：如果有足够的数据，此模型会收敛到最优结果。尽管如此，我们还是可以轻松地将可学习的参数集成到注意力汇聚中

$$\begin{aligned} f(x) &=\sum_{i=1}^{n} \alpha\left(x, x_{i}\right) y_{i} \\ &=\sum_{i=1}^{n} \frac{\exp \left(-\frac{1}{2}\left(\left(x-x_{i}\right) w\right)^{2}\right)}{\sum_{j=1}^{n} \exp \left(-\frac{1}{2}\left(\left(x-x_{j}\right) w\right)^{2}\right)} y_{i} \\ &=\sum_{i=1}^{n} \operatorname{softmax}\left(-\frac{1}{2}\left(\left(x-x_{i}\right) w\right)^{2}\right) y_{i} . \end{aligned}$$

注意这里 $w$ 只是一个标量，如果 $w$ 越大说明越注意近距离的键值。这里提一下，一个训练样本的输入都会和除自己以外的所有训练样本的“键－值”对进行计算，如果加入自己的 key 那么训练结果可想而知，就是给自己的 key 加入很大的权重

注意力可视化

平均池化可以被视为输入的加权平均值，只是权重相等。而注意力池化则是真正的加权平均，其中权重是在给定的查询 query 和不同的键 key 之间计算得出的。教材这里写了一些代码，在之后用于注意力可视化，以描绘图像 $weight = f(query, key)$ ，这里直接看看上一小节中的非参 N-W 核回归（左侧） & 带参 N-W 核回归（右侧）的图像

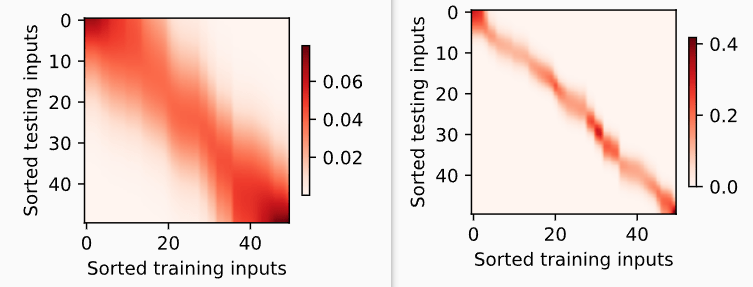
可以明显看到注意力权重在 $query = key$ 的时候加重了

注意力评分函数

我们可以将上一节中的高斯核指数部分视为注意力评分函数（attention scoring function），简称评分函数（scoring function），然后把这个函数的输出结果输入到 softmax 函数中进行运算（这样就能使评分以概率分布形式展现，换句话说就是使权重的和为一）

让 score function 表示更加数学化

$$\alpha\left(\mathbf{q}, \mathbf{k}_{i}\right)=\operatorname{softmax}\left(a\left(\mathbf{q}, \mathbf{k}_{i}\right)\right)=\frac{\exp \left(a\left(\mathbf{q}, \mathbf{k}_{i}\right)\right)}{\sum_{j=1}^{m} \exp \left(a\left(\mathbf{q}, \mathbf{k}_{j}\right)\right)} \in \mathbb{R}$$

此时注意力汇聚函数 $f$ 就被表示为

$$f\left(\mathbf{q},\left(\mathbf{k}_{1}, \mathbf{v}_{1}\right), \ldots,\left(\mathbf{k}_{m}, \mathbf{v}_{m}\right)\right)=\sum_{i=1}^{m} \alpha\left(\mathbf{q}, \mathbf{k}_{i}\right) \mathbf{v}_{i} \in \mathbb{R}^{v}$$

在本节中，我们将介绍两个流行的评分函数，稍后将用他们来实现更复杂的注意力机制

掩蔽 softmax 操作

在某些情况下，并非所有的值都应该被纳入到注意力汇聚中。例如，为了高效处理小批量数据集，某些文本序列被填充了没有意义的特殊词元。为了仅将有意义的词元作为值来获取注意力汇聚，我们可以指定一个有效序列长度，以便在计算softmax时过滤掉超出指定范围的位置。看看大概效果是什么样子

# (batch, num_query, num_key)
masked_softmax(torch.rand(2, 2, 4), torch.tensor([2, 3]))

tensor([[[0.4527, 0.5473, 0.0000, 0.0000],
         [0.3458, 0.6542, 0.0000, 0.0000]],

        [[0.4151, 0.3528, 0.2321, 0.0000],
         [0.2604, 0.2631, 0.4765, 0.0000]]])

加性注意力

当查询和键是不同长度的矢量时， 我们可以使用加性注意力（additive attention）作为评分函数

$$a(\mathbf{q}, \mathbf{k})=\mathbf{w}_{v}^{\top} \tanh \left(\mathbf{W}_{q} \mathbf{q}+\mathbf{W}_{k} \mathbf{k}\right) \in \mathbb{R}$$

上代码，注意代码中对 query, key, value 的数量（sequence length / time step）具有一般性，它们的形状表示为 (batch_size, seq_len, feature)，教材中使用的 query, key, value 具体形状为：(2, 1, 20)，(2, 10, 2) 和 (2, 10, 4)，具体走一遍会比较清晰

#@save
class AdditiveAttention(nn.Module):
    """加性注意力"""
    def __init__(self, key_size, query_size, num_hiddens, dropout, **kwargs):
        super(AdditiveAttention, self).__init__(**kwargs)
        # 无偏置
        # nn.Linear 的 input 为 (*,H_in) * 代表任意数量的维度，包括 none 
        self.W_k = nn.Linear(key_size, num_hiddens, bias=False)
        self.W_q = nn.Linear(query_size, num_hiddens, bias=False)
        self.w_v = nn.Linear(num_hiddens, 1, bias=False)
        self.dropout = nn.Dropout(dropout)

    def forward(self, queries, keys, values, valid_lens):
        queries, keys = self.W_q(queries), self.W_k(keys)
        # 在维度扩展后，
        # queries的形状：(batch_size，查询的个数，1，num_hidden)
        # key的形状：(batch_size，1，“键－值”对的个数，num_hiddens)
        # 使用广播方式进行求和
        features = queries.unsqueeze(2) + keys.unsqueeze(1)
        features = torch.tanh(features)
        # self.w_v仅有一个输出，因此从形状中移除最后那个维度。
        # scores的形状：(batch_size，查询的个数，“键-值”对的个数)
        scores = self.w_v(features).squeeze(-1)
        self.attention_weights = masked_softmax(scores, valid_lens)
        # values的形状：(batch_size，“键－值”对的个数，值的维度)
        # 使用 batch matrix multiplication（@ 重载符既可以计算 mm 又可以计算 bmm）
        # 使用 dropout 进行正则化
        return torch.bmm(self.dropout(self.attention_weights), values)

运行下面的代码

queries, keys = torch.normal(0, 1, (2, 1, 20)), torch.ones((2, 10, 2))
# values的小批量，两个值矩阵是相同的
values = torch.arange(40, dtype=torch.float32).reshape(1, 10, 4).repeat(
    2, 1, 1)
valid_lens = torch.tensor([2, 6])

attention = AdditiveAttention(key_size=2, query_size=20, num_hiddens=8,
                              dropout=0.1)
attention.eval()
attention(queries, keys, values, valid_lens)

结果如下

tensor([[[ 2.0000,  3.0000,  4.0000,  5.0000]],

        [[10.0000, 11.0000, 12.0000, 13.0000]]], grad_fn=<BmmBackward0>)

缩放点积注意力

使用点积可以得到计算效率更高的评分函数，但是点积操作要求查询和键具有相同的长度 d

假设查询和键的所有元素都是独立的随机变量， 并且都满足零均值和单位方差， 那么两个向量的点积的均值为0，方差为 d。为确保无论向量长度如何，点积的方差在不考虑向量长度的情况下仍然是1，我们将点积除以 $\sqrt d$

$$a(\mathbf{q}, \mathbf{k})=\mathbf{q}^{\top} \mathbf{k} / \sqrt{d}$$

查询 $Q\in R^{n\times d}$，键 $K \in R^{m \times d}$ ，值 $V \in R^{m \times v}$ 的缩放点积注意力（scaled dot-product attention）是：

$$\operatorname{softmax}\left(\frac{\mathbf{Q K}^{\top}}{\sqrt{d}}\right) \mathbf{V} \in \mathbb{R}^{n \times v}$$

它的代码就相对简单一些

#@save
class DotProductAttention(nn.Module):
    """缩放点积注意力"""
    def __init__(self, dropout, **kwargs):
        super(DotProductAttention, self).__init__(**kwargs)
        self.dropout = nn.Dropout(dropout)

    # queries的形状：(batch_size，查询的个数，d)
    # keys的形状：(batch_size，“键－值”对的个数，d)
    # values的形状：(batch_size，“键－值”对的个数，值的维度)
    # valid_lens的形状:(batch_size，)或者(batch_size，查询的个数)
    def forward(self, queries, keys, values, valid_lens=None):
        d = queries.shape[-1]
        # 设置transpose_b=True为了交换keys的最后两个维度
        scores = torch.bmm(queries, keys.transpose(1,2)) / math.sqrt(d)
        self.attention_weights = masked_softmax(scores, valid_lens)
        return torch.bmm(self.dropout(self.attention_weights), values)

Bahdanau 注意力

之前教材讨论了机器翻译问题：通过编码器-解码器架构，用于序列到序列学习。具体来说，编码器将长度可变的序列转换为固定形状的上下文变量，然后解码器根据生成的词元和上下文变量按词元生成输出（目标）序列词元。然而，即使并非所有输入（源）词元都对解码某个词元都有用，但我们在每个解码步骤中仍使用编码相同的上下文变量

有什么方法能在不同解码步骤中，使用不同的上下文变量呢？这个时候 Bahdanau 注意力机制就登场了，下面具体来看看吧

模型

上下文变量任意解码时间步 $t’$ 会被替换为 $c_{t’}$

$$\mathbf{c}_{t^{\prime}}=\sum_{t=1}^{T} \alpha\left(\mathbf{s}_{t^{\prime}-1}, \mathbf{h}_{t}\right) \mathbf{h}_{t}$$

其中，$h_t$ 为编码器 t 时间步的隐状态，它即使 key 又是 value；$s_{t’-1}$ 为解码器 $t’-1$ 时刻步的隐状态；注意力权重 $\alpha$ 是之前定义的加性注意力打分函数。看一下模型代码

class Seq2SeqAttentionDecoder(AttentionDecoder):
    def __init__(self, vocab_size, embed_size, num_hiddens, num_layers,
                 dropout=0, **kwargs):
        super(Seq2SeqAttentionDecoder, self).__init__(**kwargs)
        self.attention = d2l.AdditiveAttention(
            num_hiddens, num_hiddens, num_hiddens, dropout)
        self.embedding = nn.Embedding(vocab_size, embed_size)
        self.rnn = nn.GRU(
            embed_size + num_hiddens, num_hiddens, num_layers,
            dropout=dropout)
        self.dense = nn.Linear(num_hiddens, vocab_size)

    def init_state(self, enc_outputs, enc_valid_lens, *args):
        # outputs的形状为(batch_size，num_steps，num_hiddens).
        # hidden_state的形状为(num_layers，batch_size，num_hiddens)
        outputs, hidden_state = enc_outputs
        return (outputs.permute(1, 0, 2), hidden_state, enc_valid_lens)

    def forward(self, X, state):
        # X.shape = (num_batch, num_steps) 存储词元的索引
        # enc_outputs的形状为(batch_size,num_steps,num_hiddens).
        # hidden_state的形状为(num_layers,batch_size,
        # num_hiddens)
        enc_outputs, hidden_state, enc_valid_lens = state
        # 输出X的形状为(num_steps,batch_size,embed_size)
        X = self.embedding(X).permute(1, 0, 2)
        outputs, self._attention_weights = [], []
        for x in X:
            # query的形状为(batch_size,1,num_hiddens)
            query = torch.unsqueeze(hidden_state[-1], dim=1)
            # context的形状为(batch_size,1,num_hiddens)
            context = self.attention(
                query, enc_outputs, enc_outputs, enc_valid_lens)
            # 在特征维度上连结
            x = torch.cat((context, torch.unsqueeze(x, dim=1)), dim=-1)
            # 将x变形为(1,batch_size,embed_size+num_hiddens)
            out, hidden_state = self.rnn(x.permute(1, 0, 2), hidden_state)
            outputs.append(out)
            self._attention_weights.append(self.attention.attention_weights)
        # 全连接层变换后，outputs的形状为
        # (num_steps,batch_size,vocab_size)
        outputs = self.dense(torch.cat(outputs, dim=0))
        return outputs.permute(1, 0, 2), [enc_outputs, hidden_state,
                                          enc_valid_lens]

    @property
    def attention_weights(self):
        return self._attention_weights

关于 nn.Embedding，其实在之前 seq2seq 中的代码也有使用，整理几个点：

1. Embedding 层将每个词元转化为 embed_size 维度的向量（也称为词向量）
2. Embedding layer 存储了一个参数矩阵 (vocab_size, embed_size) 是可以随着训练更新的
3. 经过训练之后相似词元的词向量可能会变得更接近

来看看其中的权重是什么样子的吧，输入和输出分别为： i'm home . => je suis chez moi .

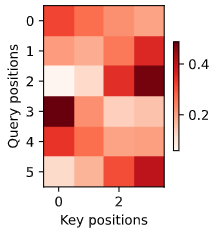
应该是加入了 <eos> 特殊词元，所以 (key positions, Query positions) = (3+1, 5+1)

多头注意力

多头注意力这一部分的视频讲解是在 Transformer 中进行的 bilibili

在实践中，当给定相同的查询、键和值的集合时， 我们希望模型可以基于相同的注意力机制学习到不同的行为，然后将不同的行为作为知识组合起来，捕获序列内各种范围的依赖关系（例如，短距离依赖和长距离依赖关系）

对于其中一个头 $i$ 的操作简述如下：是对 query, key, value 先使用全连接层进行维度转换，转换到一个相同的维度 $p_v$，然后再使用缩放点积注意力。每一个头都将进行这样的操作，假设有 $m$ 个头，那么就会得到 $m$ 个注意力汇聚输出 $h_i, i=1,…,m$，最后将所有的 $h_i$ 连接起来，使用一个全连接层进行特征组合得到最终的输出，数学形式如下：

$$\mathbf{h}_{i}=f\left(\mathbf{W}_{i}^{(q)} \mathbf{q}, \mathbf{W}_{i}^{(k)} \mathbf{k}, \mathbf{W}_{i}^{(v)} \mathbf{v}\right) \in \mathbb{R}^{p_{v}} \\ \mathbf{W}_{o}\left[\begin{array}{c} \mathbf{h}_{1} \\ \vdots \\ \mathbf{h}_{h} \end{array}\right] \in \mathbb{R}^{p_{o}}$$

这里 $W_0$ 是一个 $p_0 \times p_0$ 的矩阵，$p_0 = \text{number of heads} \times p_v$，图示如下

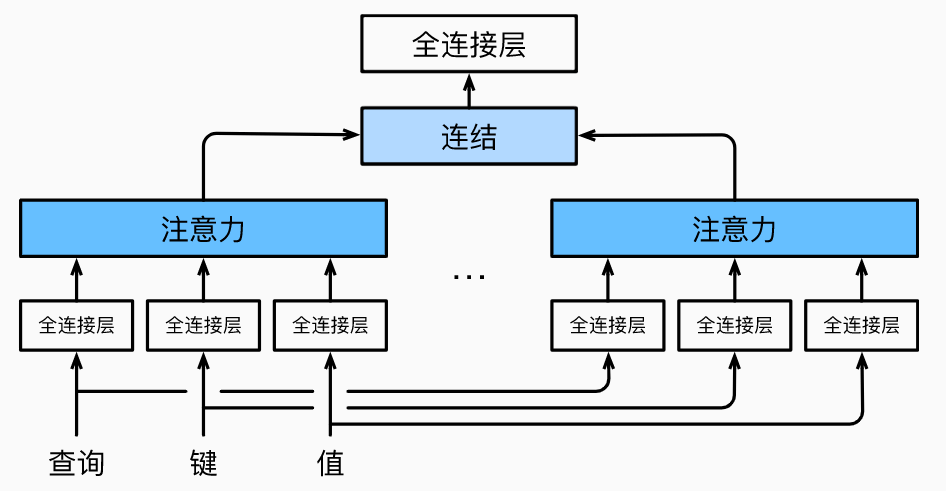
在使用代码实现的时候发现，可以把 num_heads 个 $W_{i}q$ 使用一个大的 $W_q$ 代替，然后将变换后的特征进行分割即可。其他两个矩阵同理，这样便于并行处理，并且代码更简洁

#@save
class MultiHeadAttention(nn.Module):
    """多头注意力"""
    def __init__(self, key_size, query_size, value_size, num_hiddens,
                 num_heads, dropout, bias=False, **kwargs):
        super(MultiHeadAttention, self).__init__(**kwargs)
        self.num_heads = num_heads
        self.attention = d2l.DotProductAttention(dropout)
        self.W_q = nn.Linear(query_size, num_hiddens, bias=bias)
        self.W_k = nn.Linear(key_size, num_hiddens, bias=bias)
        self.W_v = nn.Linear(value_size, num_hiddens, bias=bias)
        self.W_o = nn.Linear(num_hiddens, num_hiddens, bias=bias)

    def forward(self, queries, keys, values, valid_lens):
        queries = transpose_qkv(self.W_q(queries), self.num_heads)
        keys = transpose_qkv(self.W_k(keys), self.num_heads)
        values = transpose_qkv(self.W_v(values), self.num_heads)

        if valid_lens is not None:
            # 在轴0，将第一项（标量或者矢量）复制num_heads次
            valid_lens = torch.repeat_interleave(
                valid_lens, repeats=self.num_heads, dim=0)

        # output的形状:(batch_size*num_heads，num_query,
        # num_hiddens/num_heads)
        output = self.attention(queries, keys, values, valid_lens)

        output_concat = transpose_output(output, self.num_heads)
        return self.W_o(output_concat)

#@save
def transpose_qkv(X, num_heads):
    """为了多注意力头的并行计算而变换形状"""
    X = X.reshape(X.shape[0], X.shape[1], num_heads, -1)

    X = X.permute(0, 2, 1, 3)

    # 最终输出的形状:(batch_size*num_heads, num_query or num_keys,
    # num_hiddens/num_heads)
    return X.reshape(-1, X.shape[2], X.shape[3])


#@save
def transpose_output(X, num_heads):
    """逆转transpose_qkv函数的操作"""
    X = X.reshape(-1, num_heads, X.shape[1], X.shape[2])
    X = X.permute(0, 2, 1, 3)
    return X.reshape(X.shape[0], X.shape[1], -1)

自注意力和位置编码

终于进入自注意力部分了，离 transformer 只有一步之遥！

在深度学习中，我们经常使用卷积神经网络（CNN）或循环神经网络（RNN）对序列进行编码。想象一下，有了注意力机制之后，我们将词元序列输入注意力池化层中，同一组词元同时充当查询、键和值。每个查询都会关注所有的键－值对并生成一个注意力输出。由于查询、键和值来自同一组输入，因此被称为 自注意力（self-attention）在本节中，我们将使用自注意力进行序列编码，以及如何使用序列的顺序作为补充信息

自注意力

给定一个由词元组成的输入序列，其中任意 $x_i \in R^ d$。该序列的自注意力输出为一个长度相同的序列：

$$\mathbf{y}_{i}=f\left(\mathbf{x}_{i},\left(\mathbf{x}_{1}, \mathbf{x}_{1}\right), \ldots,\left(\mathbf{x}_{n}, \mathbf{x}_{n}\right)\right) \in \mathbb{R}^{d}$$

比较卷积神经网络、循环神经网络和自注意力

下图为三者计算的图示

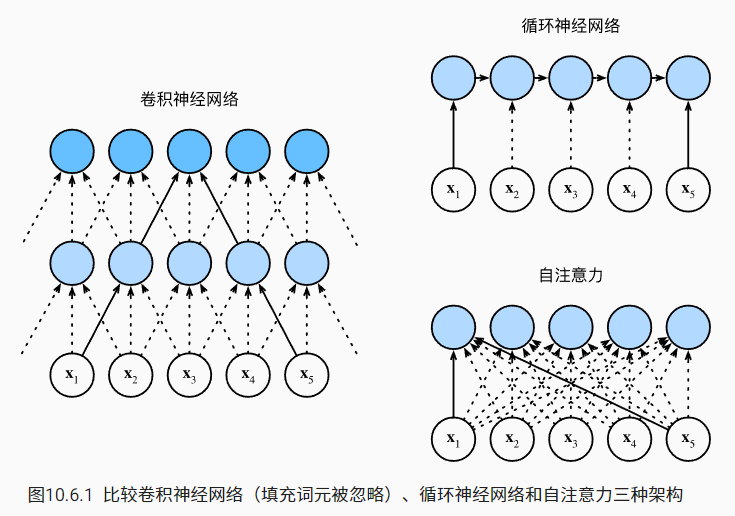
现在让我们比较这三个架构，目标都是将由 n 个词元组成的序列映射到另一个长度相等的序列，其中的每个输入词元或输出词元都由 d 维向量表示。具体来说，我们将比较的是卷积神经网络、循环神经网络和自注意力这几个架构的计算复杂性、顺序操作和最大路径长度。请注意，顺序操作会妨碍并行计算，而任意的序列位置组合之间的路径越短，则能更轻松地学习序列中的远距离依赖关系

下面这个表依然来自于沐神视频 bilibili，非常清晰地对比了三者的关系，其中 k 是一维卷积核的 kernel size

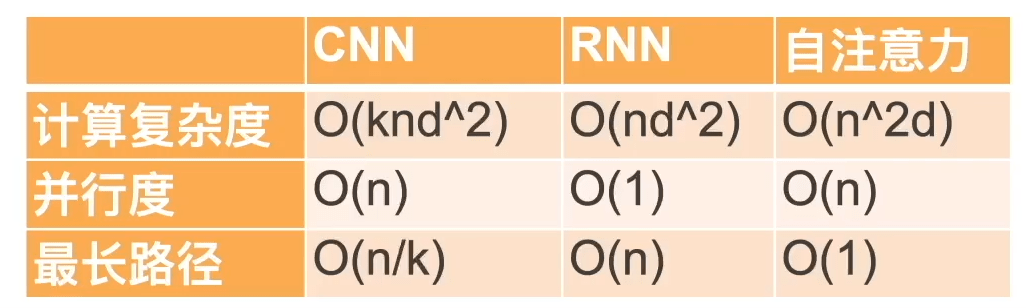
稍微解释一下：

1. 最长路径中的路径为：两个词元进行信息传递的计算次数
2. 循环神经网络的隐状态时， d×d 权重矩阵和 d 维隐状态的乘法计算复杂度为 $O(d^2)$
3. 在自注意力中，查询、键和值都是 n×d 矩阵。 并且使用缩放点积注意力，故自注意力计算复杂度为 $O(n^2d)$，并且由于使用的是矩阵乘法，而矩阵乘法的并行度为 $O(n)$

总而言之，卷积神经网络和自注意力都拥有并行计算的优势，而且自注意力的最大路径长度最短。但是因为其计算复杂度是关于序列长度的二次方，所以在很长的序列中计算会非常慢

位置编码

不同于 CNN 和 RNN，以上得到的自注意力计算结果是不包含位置（顺序）信息的。也就是说换个输入顺序，得到的结果还是那些结果，这显然不是我们想要的，接下来，我们描述的是基于正弦函数和余弦函数的固定位置编码（不得不吐槽一下这个编码真的略微抽象

以下是我的个人理解：对于一个序列 range(n)，我需要使用 d 个维度对其位置进行编码，采取如下编码形式， $p_{i,j}$ 即是第 i 个位置的第 j 个维度的编码数

$$\begin{aligned} p_{i, 2 j} &=\sin \left(\frac{i}{10000^{2 j / d}}\right) \\ p_{i, 2 j+1} &=\cos \left(\frac{i}{10000^{2 j / d}}\right) \end{aligned}$$

第一次看这个编码真的太蒙圈了，不过教材举了一个例子：绝对位置信息。也就是我们使用 d 位二进制对序列 range(n) 的位置进行编码，这样来看是不是就简单不少了

# d = 5
0的二进制是：00000
1的二进制是：00001
2的二进制是：00010
3的二进制是：00011
4的二进制是：00100
5的二进制是：00101
6的二进制是：00110
7的二进制是：00111

越高位的数字变化得越慢，一共能够编码 $2^n$ 个数。那如果我们用 d 维 (0, 1) 之间的数去对位置进行编码是不是也可以呢？教材中的位置编码就属于其中一种。还可以从平面空间的角度来进行理解，假设有 d 个维度，此时我们画出 d/2 个平面

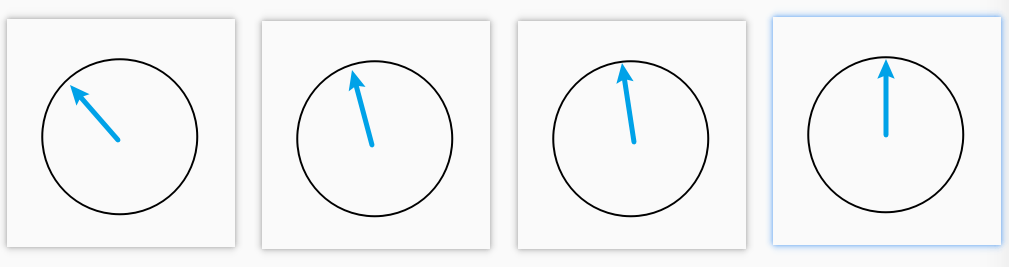
旋转角度就是对应着 (cos, sin)，随着位数越高每次 i 进一时，旋转的幅度越小。下面是 position 和 endoding dimension 的热力图

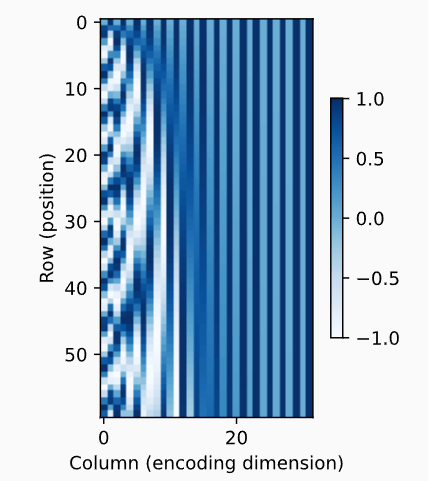
我已经尽力去理解了…但是还是有点云里雾里，不过还是先继续前行吧

Transformer

与 CNN 和 RNN 比较，自注意力同时具有并行计算和最短的最大路径长度这两个优势，因此，使用自注意力来设计深度架构是很有吸引力的。尽管 transformer 最初是应用于在文本数据上的序列到序列学习，但现在已经推广到各种现代的深度学习中，例如语言、视觉、语音和强化学习领域

我认为这里贴英文的图示比较好，第一次看这个图肯定是一头雾水，可以先看代码，了解每个模块的结构，然后再拼起来

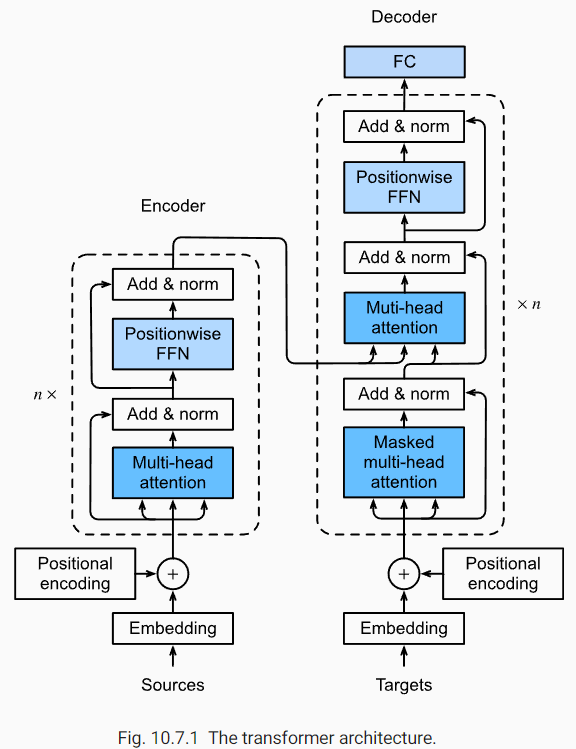
基于位置的前馈网络 （Positionwise FFN）

名字很酷，实际上是两个全连接层

#@save
class PositionWiseFFN(nn.Module):
    """基于位置的前馈网络"""
    def __init__(self, ffn_num_input, ffn_num_hiddens, ffn_num_outputs,
                 **kwargs):
        super(PositionWiseFFN, self).__init__(**kwargs)
        self.dense1 = nn.Linear(ffn_num_input, ffn_num_hiddens)
        self.relu = nn.ReLU()
        self.dense2 = nn.Linear(ffn_num_hiddens, ffn_num_outputs)

    def forward(self, X):
        return self.dense2(self.relu(self.dense1(X)))

残差连接和层规范化（add & norm）

残差连接是很常见的网络结构，这里主要讲讲规范化使用的是 LayerNorm。假设数据 $X$ 的形状为 (batch, num_steps, channels)，BatchNorm 针对的是 batch 维度，最后得到的均值和方差形状是 (num_steps, channels)

但问题来了，在计算机视觉中 num_steps 一般代表的是图片的形状 (H, W) 所以是一个固定的值，而在序列模型中，由于每个样本的时间步可能不一样

所以 LayerNorm 针对的是 num_steps 维度（更宽泛的讲可以是除了 batch 以外的其他维度），最终得到的均值和方差形状是 (batch, channels) or (batch,)，这就保证了统一性，因为 batch & channel 一般是一个固定值。

除了使用 LayerNorm 还使用了 dropout 正则化，下面来看看核心代码（LayerNorm 输入是 normalized_shape，我理解为计算单个统计值，数据所需的形状）

#@save
class AddNorm(nn.Module):
    """残差连接后进行层规范化"""
    def __init__(self, normalized_shape, dropout, **kwargs):
        super(AddNorm, self).__init__(**kwargs)
        self.dropout = nn.Dropout(dropout)
        self.ln = nn.LayerNorm(normalized_shape)

    def forward(self, X, Y):
        return self.ln(self.dropout(Y) + X)

编码器

EncoderBlock

有了以上两个模块：FFN & AddNorm，再加上之前介绍的多头注意力模块，就能够构建一个完整的 transformer 编码器模块

#@save
class EncoderBlock(nn.Module):
    """transformer编码器块"""
    def __init__(self, key_size, query_size, value_size, num_hiddens,
                 norm_shape, ffn_num_input, ffn_num_hiddens, num_heads,
                 dropout, use_bias=False, **kwargs):
        super(EncoderBlock, self).__init__(**kwargs)
        self.attention = d2l.MultiHeadAttention(
            key_size, query_size, value_size, num_hiddens, num_heads, dropout,
            use_bias)
        self.addnorm1 = AddNorm(norm_shape, dropout)
        self.ffn = PositionWiseFFN(
            ffn_num_input, ffn_num_hiddens, num_hiddens)
        self.addnorm2 = AddNorm(norm_shape, dropout)

    def forward(self, X, valid_lens):
        Y = self.addnorm1(X, self.attention(X, X, X, valid_lens))
        return self.addnorm2(Y, self.ffn(Y))

transformer 一个很好的性质是：编码器中的任何层都不会改变其输入的形状！

X = torch.ones((2, 100, 24))
valid_lens = torch.tensor([3, 2])
encoder_blk = EncoderBlock(24, 24, 24, 24, [100, 24], 24, 48, 8, 0.5)
encoder_blk.eval()
encoder_blk(X, valid_lens).shape
# torch.Size([2, 100, 24])

TransformerEncoder

有了单个模块之后，就可以将它们堆叠起来获得更强大编码器，当然这里还有两个需要注意的点：

1. Positional encoding，给每一个序列使用之前所将的三角函数位置编码
2. 由于 embedding 的数值是经过归一化的，也就是说除以了 $\sqrt{d}$，而 Positional encoding 的值是 (-1, 1) 之间的三角函数，为了让两个数相加（加入位置信息），并且让二者的数值大小相差更小，则需要将 embedding 再乘以长度 $\sqrt{d}$ 以还原

代码如下

#@save
class TransformerEncoder(d2l.Encoder):
    """transformer编码器"""
    def __init__(self, vocab_size, key_size, query_size, value_size,
                 num_hiddens, norm_shape, ffn_num_input, ffn_num_hiddens,
                 num_heads, num_layers, dropout, use_bias=False, **kwargs):
        super(TransformerEncoder, self).__init__(**kwargs)
        self.num_hiddens = num_hiddens
        self.embedding = nn.Embedding(vocab_size, num_hiddens)
        self.pos_encoding = d2l.PositionalEncoding(num_hiddens, dropout)
        self.blks = nn.Sequential()
        for i in range(num_layers):
            self.blks.add_module("block"+str(i),
                EncoderBlock(key_size, query_size, value_size, num_hiddens,
                             norm_shape, ffn_num_input, ffn_num_hiddens,
                             num_heads, dropout, use_bias))

    def forward(self, X, valid_lens, *args):
        # 因为位置编码值在-1和1之间，
        # 因此嵌入值乘以嵌入维度的平方根进行缩放，
        # 然后再与位置编码相加。
        X = self.pos_encoding(self.embedding(X) * math.sqrt(self.num_hiddens))
        self.attention_weights = [None] * len(self.blks)
        for i, blk in enumerate(self.blks):
            X = blk(X, valid_lens)
            self.attention_weights[
                i] = blk.attention.attention.attention_weights
        return X

下面我们指定了超参数来创建一个两层的 transformer 编码器。Transformer 编码器输出的形状是（批量大小，时间步数目，num_hiddens）

encoder = TransformerEncoder(
    200, 24, 24, 24, 24, [100, 24], 24, 48, 8, 2, 0.5)
encoder.eval()
encoder(torch.ones((2, 100), dtype=torch.long), valid_lens).shape
# torch.Size([2, 100, 24])

解码器

DecoderBlock

同样的，先实现单个解码器模块。其实基本的模块之前已经全部实现了，细节上的不同是：

1. 与 encoder 相比，decoder 先使用自注意力汇聚对 targets 输入进行编码。然后将该编码作为 query、将 encoder 的输出作为 key & value，输入到多头注意力汇聚中
2. 同 seq2seq 一样，在进行解码时不应该看到该时间步及其之后的信息，所以需要掩码 dec_valid_lens，以保持其自回归属性

具体代码如下

class DecoderBlock(nn.Module):
    """解码器中第 i 个块"""
    def __init__(self, key_size, query_size, value_size, num_hiddens,
                 norm_shape, ffn_num_input, ffn_num_hiddens, num_heads,
                 dropout, i, **kwargs):
        super(DecoderBlock, self).__init__(**kwargs)
        self.i = i
        self.attention1 = d2l.MultiHeadAttention(
            key_size, query_size, value_size, num_hiddens, num_heads, dropout)
        self.addnorm1 = AddNorm(norm_shape, dropout)
        self.attention2 = d2l.MultiHeadAttention(
            key_size, query_size, value_size, num_hiddens, num_heads, dropout)
        self.addnorm2 = AddNorm(norm_shape, dropout)
        self.ffn = PositionWiseFFN(ffn_num_input, ffn_num_hiddens,
                                   num_hiddens)
        self.addnorm3 = AddNorm(norm_shape, dropout)

    def forward(self, X, state):
        enc_outputs, enc_valid_lens = state[0], state[1]
        # 训练阶段，输出序列的所有词元都在同一时间处理，
        # 因此 `state[2][self.i]` 初始化为 `None`。
        # 预测阶段，输出序列是通过词元一个接着一个解码的，
        # 因此 `state[2][self.i]` 包含着直到当前时间步第 `i` 个块解码的输出表示
        if state[2][self.i] is None:
            key_values = X
        else:
            key_values = torch.cat((state[2][self.i], X), axis=1)
        state[2][self.i] = key_values
        if self.training:
            batch_size, num_steps, _ = X.shape
            # `dec_valid_lens` 的开头: (`batch_size`, `num_steps`),
            # 其中每一行是 [1, 2, ..., `num_steps`]
            dec_valid_lens = torch.arange(
                1, num_steps + 1, device=X.device).repeat(batch_size, 1)
        else:
            dec_valid_lens = None

        # 自注意力
        X2 = self.attention1(X, key_values, key_values, dec_valid_lens)
        Y = self.addnorm1(X, X2)
        # 编码器－解码器注意力。
        # `enc_outputs` 的开头: (`batch_size`, `num_steps`, `num_hiddens`)
        Y2 = self.attention2(Y, enc_outputs, enc_outputs, enc_valid_lens)
        Z = self.addnorm2(Y, Y2)
        return self.addnorm3(Z, self.ffn(Z)), state

为了便于在“编码器－解码器”注意力中进行缩放点积计算和残差连接中进行加法计算，编码器和解码器的特征维度都是 num_hiddens，所以说 decoder 也是不改变数据形状的

decoder_blk = DecoderBlock(24, 24, 24, 24, [100, 24], 24, 48, 8, 0.5, 0)
decoder_blk.eval()
X = torch.ones((2, 100, 24))
state = [encoder_blk(X, valid_lens), valid_lens, [None]]
decoder_blk(X, state)[0].shape
# torch.Size([2, 100, 24])

TransformerDecoder

下面将多个 decoder 组合起来，并保存注意力权重用于可视化

class TransformerDecoder(d2l.AttentionDecoder):
    def __init__(self, vocab_size, key_size, query_size, value_size,
                 num_hiddens, norm_shape, ffn_num_input, ffn_num_hiddens,
                 num_heads, num_layers, dropout, **kwargs):
        super(TransformerDecoder, self).__init__(**kwargs)
        self.num_hiddens = num_hiddens
        self.num_layers = num_layers
        self.embedding = nn.Embedding(vocab_size, num_hiddens)
        self.pos_encoding = d2l.PositionalEncoding(num_hiddens, dropout)
        self.blks = nn.Sequential()
        for i in range(num_layers):
            self.blks.add_module("block"+str(i),
                DecoderBlock(key_size, query_size, value_size, num_hiddens,
                             norm_shape, ffn_num_input, ffn_num_hiddens,
                             num_heads, dropout, i))
        self.dense = nn.Linear(num_hiddens, vocab_size)

    def init_state(self, enc_outputs, enc_valid_lens, *args):
        return [enc_outputs, enc_valid_lens, [None] * self.num_layers]

    def forward(self, X, state):
        X = self.pos_encoding(self.embedding(X) * math.sqrt(self.num_hiddens))
        self._attention_weights = [[None] * len(self.blks) for _ in range (2)]
        for i, blk in enumerate(self.blks):
            X, state = blk(X, state)
            # 解码器自注意力权重
            self._attention_weights[0][
                i] = blk.attention1.attention.attention_weights
            # “编码器－解码器”自注意力权重
            self._attention_weights[1][
                i] = blk.attention2.attention.attention_weights
        return self.dense(X), state

    @property
    def attention_weights(self):
        return self._attention_weights

下面来看看三个 Multi-attention 的可视化结果，主要是体会 valid_len 的效果

1. Encoder self-attention weights

   

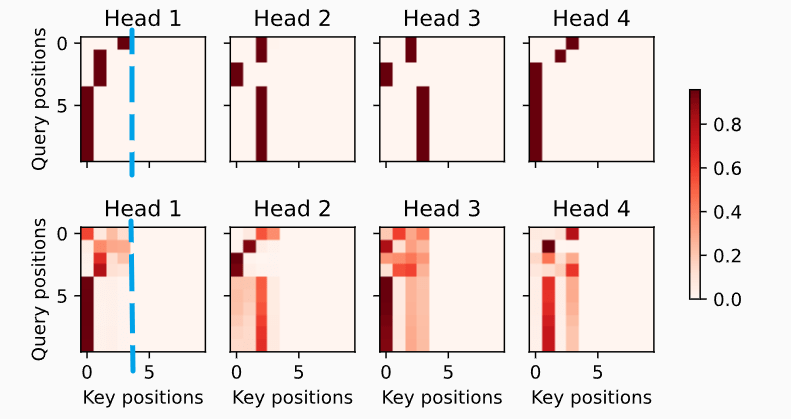
   可以看到在某个 key positions 过后是没有注意力权重的，是因为之后的 key 都是 词元，不需要进行注意力计算

2. Decoder self-attention weights

   

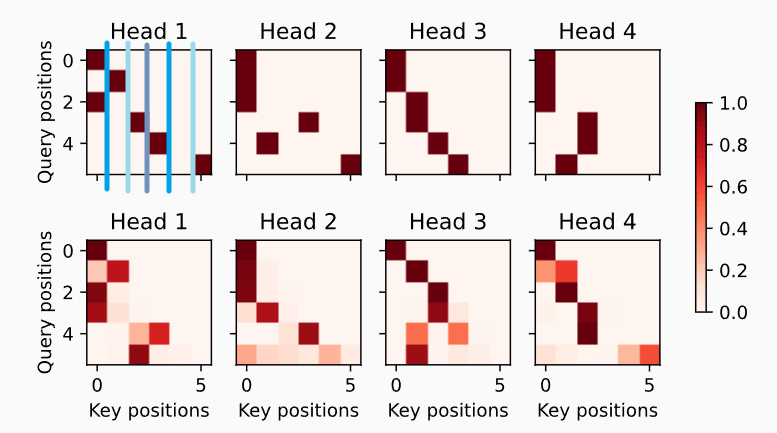
   由于 decoder 的每个 valid_len 是随着时间步逐渐增加的，所以可以看到 self-attention weights 似乎整体是呈下三角形状

3. Encoder-decoder attention weights

   

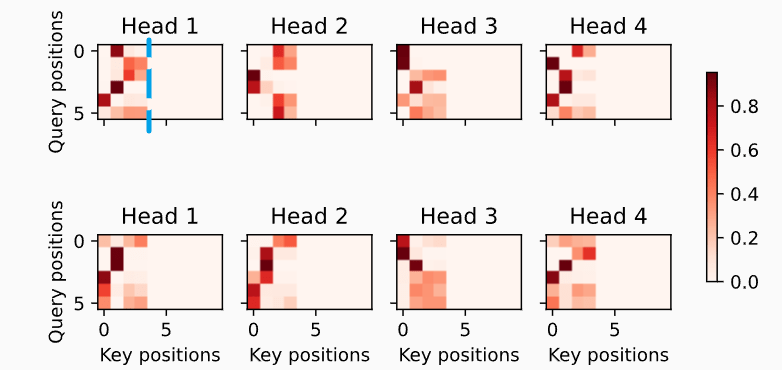
   又出现了 encoder self-attention 中的情况，超过某个 key position 就没有权重了，因为只有这么多个 key (source time step)

感言

可算是完成了总结😭😭虽然看得还是比较粗糙，但是总归是有些概念了。在沐神读论文的视频 bilibili 中讲到：虽然 transformer 论文叫做 Attention Is All You Need，但事实上各个结构都是很重要的，例如：残差连接和层规规范化在训练深度网络时是非常重要的。Transformer (attention) 整体来看仍是一个发展初期的架构，在未来或许有更多的架构出现，一起期待吧