D2L 04 多层感知机

多层感知机

线性模型的表示能力是有限的，如果加入隐藏层和非线性运算，模型的表示能力将大大增加。事实上如果隐藏层的节点足够多，模型将能够拟合任意的连续函数 $f(·)$，这就是万能/通用近似 universal approximation

参考链接：bilibili link 直观简述了为什么 hidden layer + ReLU 能够拟合任意连续函数，看完就有感觉了

Pytorch 实现

import torch
from torch import nn
import numpy as np

from torch.utils.data.dataloader import DataLoader
from torch.utils.data.sampler import SubsetRandomSampler
from torch.optim import SGD
from utils import get_dataset, train


train_dataset = get_dataset(train=True)
test_dataset = get_dataset(train=False)
data = train_dataset[0]
  
MLP = nn.Sequential(
    nn.Flatten(),
    nn.Linear(28*28, 256),
    nn.ReLU(),
    nn.Linear(256, 10)
)

batch_size, lr, num_epochs = 256, 0.1, 10
loss = nn.CrossEntropyLoss()
optim = SGD(MLP.parameters(), lr=lr)

NUM = len(train_dataset)
sampler = SubsetRandomSampler(np.arange(NUM))
train_loader = DataLoader(train_dataset, batch_size=batch_size, sampler=sampler)

train(MLP, train_loader, num_epochs, optim, loss)

其中我自己写了一个 utils 文件，包含一些常规功能，这里不贴出来了

模型选择、欠拟合和过拟合

训练误差和泛化误差

将模型在训练数据上拟合得比在潜在分布中更接近的现象称为过拟合（overfitting），用于对抗过拟合的技术称为正则化（regularization）

为了进一步讨论这一现象，我们需要了解训练误差和泛化误差。训练误差（training error）是指，我们的模型在训练数据集上计算得到的误差。泛化误差（generalization error）是指，当我们将模型应用在同样从原始样本的分布中抽取的无限多的数据样本时，我们模型误差的期望

在实际中，我们只能通过将模型应用于一个独立的测试集来估计泛化误差，该测试集由随机选取的、未曾在训练集中出现的数据样本构成

过拟合和欠拟合

欠拟合是指模型无法继续减少训练误差。过拟合是指训练误差远小于验证误差

一般来讲模型越复杂，训练集越简单，越容易过拟合。教材使用了多项式回归来简要说明了这一现象：使用更高阶的多项式，通过参数调整，很容易（过）拟合一个函数

利用验证集进行模型选择

为了确定候选模型中的最佳模型，我们通常会使用验证集。这个问题的一个流行的解决方案是采用 K 折交叉验证。通过对 K 次实验的结果取平均来估计训练和验证误差

权重衰减

L2 正则化

权重衰减（通常称为 L2 正则化）是最广泛使用的正则化的技术之一

要保证权重”范围”比较小，最常用方法是将其范数作为惩罚项加到最小化损失的问题中。原来的训练目标最小化训练标签上的预测损失，调整为最小化预测损失和惩罚项之和

我们通过正则化常数 λ 来描述这种权衡，这是一个非负超参数，下面是 L2 正则化下的损失函数

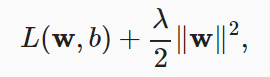
如上形式的正则化有几个好处：

1. 便于计算，没有根号

2. 使得优化算法偏向于生成在大量特征上均匀分布权重的模型，考虑下面的优化问题，可以简单理解什么是“均匀分布”

   $$min \ \sum w_i^2 \\ s.t. \sum w_i = const$$

在实例化优化器时直接通过 weight_decay 指定 weight decay 超参数。默认情况下，PyTorch 同时衰减权重和偏移。这里我们只为权重设置了 weight_decay，所以 bias 参数不会衰减

num_inputs = 784
net = nn.Sequential(nn.Linear(num_inputs, 1))
for param in net.parameters():
    param.data.normal_()
    
loss = nn.MSELoss()
num_epochs, lr = 100, 0.003
wd = 3

# 偏置参数没有衰减。
trainer = SGD([
    {"params":net[0].weight,'weight_decay': wd},
    {"params":net[0].bias}], lr=lr)

print('w的L2范数：', net[0].weight.norm().item())

学习点：

1. Pytorch 优化器可以对模型中指定参数进行权重衰减，使用一个字典组成的列表即可 torch.optim

补充：L1 正则化与稀疏参数

从凸优化的角度来看，在强对偶条件下，给定最优的正则化超参 λ*，在原函数加入惩罚项和给参数加约束是等价的

$$min\ f(x) \ s.t. \ m(x) \le 0 \\\Leftrightarrow min \ L(x, \lambda^*)$$

Dropout

这一部分的教材讲的得比较模糊…不说了直接去 bilibili 看大佬讲课！总结来说：

1. Dropout 被看作一项正则化技术，给模型加入噪声
2. Dropout 将一些输出项随机置0，常作用在 MLP 的隐藏层输出上，其中丢弃概率 p 为超参
3. 教材选择在 Dropout 输出的时候除以 (1 - p) 以保证期望不变。在 cs231n 课程中是选择在测试的时候对输出乘以 (1 - p) 以保持期望不变，二者应该是等价的

注意：Dropout 和权重衰减都是正则化技术，他们仅在训练时使用，在测试时是不使用 or 不一样的，包括之后会介绍的 batch normalization 也是一样的

dropout1, dropout2 = 0.2, 0.5

net = nn.Sequential(nn.Flatten(),
        nn.Linear(784, 256),
        nn.ReLU(),
        # 在第一个全连接层之后添加一个dropout层
        nn.Dropout(dropout1),
        nn.Linear(256, 256),
        nn.ReLU(),
        # 在第二个全连接层之后添加一个dropout层
        nn.Dropout(dropout2),
        nn.Linear(256, 10))

正向传播、反向传播和计算图

对于这一部分，我认为需要更扎实的矩阵论的知识，尤其是对于矩阵/张量求导的表示，看在之后能不能填上这部分

当然简单的结论是能够帮助我们快速前进的，下面给出矩阵乘法的反向传播结论（分子式）

$$y \in \mathbb{R}^M, x \in \mathbb{R}^N, W \in \mathbb{R}^{M\times N} \\ y=W·x, \frac{\partial{L}}{\partial y} = d_y^T\\ \text{we have } \frac{\partial L}{\partial W}=xd_y^T \\\text{and } \frac{\partial L}{\partial x}=d_y^TW$$

其实除了矩阵乘法的求导比较陌生，其他运算的求导以及链式法则应该都相对熟悉，与初高中遇到的问题是相似的

几个关于矩阵求导的参考链接：bilibili CSDN wiki Matrix calculus

这里总结几个基本法则：

1. 在求导之前一定要确定是分子式还是分母式，看个人选择，推荐分子式，更符合平时求导的直觉
2. 最重要的定律莫过于乘法求导法则 product rule 以及链式求导法则 chain rule。如果习惯按照分母式求导，那么链式求导时顺序要倒过来，并且常数在提出来时应该放在后面并且转置
3. 再来看上面得出的结论，对于 x 的求导变得相对容易，但对于 W 的求导还是有点复杂，因为是对于矩阵求导。其中会遇到 vector by matrix 的情况，这该怎么处理？事实上，这种情况需要将 upper gradient or unit 1 vector 与需要求导的 vector 相乘 $\frac{\partial (d_y^TWx)}{\partial W}$，将其转换为 scalar by matrix

之后可以结合 cs231n 中对 batch normalization 的反向传播练习以及 RNN 中的反向传播练习来加深熟练度，虽然他们都很难！

经过多次的总结，关于机器学习中常用的矩阵求导规律（依然使用分子式）：

1. 数乘法则 $$\text{vector by vector}\\ \frac{\partial \mathbf{A} \mathbf{u}}{\partial \mathbf{x}}= \mathbf A \frac{\partial \mathbf u}{\partial \mathbf x}\\ \frac{\partial u \mathbf{a}}{\partial \mathbf{x}}= \mathbf a \frac{\partial u}{\partial \mathbf x}\\ \\ \text{scalar by vector}\\ \frac{\partial \mathbf a^T \mathbf{u}}{\partial \mathbf{x}}= \mathbf a^T \frac{\partial \mathbf u}{\partial \mathbf x}$$

1. 乘法法则

   $$\text{vector by vector}\\ \frac{\partial v \mathbf{u}}{\partial \mathbf{x}}=\quad v \frac{\partial \mathbf{u}}{\partial \mathbf{x}}+\mathbf{u} \frac{\partial v}{\partial \mathbf{x}}\\ \\ \text{scalar by vector}\\ \frac{\partial \mathbf{u}^{\top} \mathbf{v}}{\partial \mathbf{x}}=\mathbf{u}^{\top} \frac{\partial \mathbf{v}}{\partial \mathbf{x}}+\mathbf{v}^{\top} \frac{\partial \mathbf{u}}{\partial \mathbf{x}}$$

1. 链式法则。 $$\text{vector by vector}\\ \frac{\partial \mathbf{f}(\mathbf{g}(\mathbf{u}))}{\partial \mathbf{x}}=\frac{\partial \mathbf{f}(\mathbf{g})}{\partial \mathbf{g}} \frac{\partial \mathbf{g}(\mathbf{u})}{\partial \mathbf{u}} \frac{\partial \mathbf{u}}{\partial \mathbf{x}}\\ \\ \text{scalar by vector}\\ \frac{\partial f(g(u))}{\partial \mathbf{x}}=\frac{\partial f(g)}{\partial g} \frac{\partial g(u)}{\partial u} \frac{\partial u}{\partial \mathbf{x}}$$

1. 向量函数为逐元素计算，求导后变为对角矩阵 $$\frac{\partial f(\mathbf x)}{\partial \mathbf x} = diag(f'(\mathbf x))$$

1. Scalar by matrix，仅给出下面一种形式，更高阶的将不再进行讨论 $$\frac{\partial \mathbf{a}^{\top} \mathbf{X} \mathbf{b}}{\partial \mathbf{X}}=\mathbf{b a}^{\top}$$

更加完善的矩阵求导体系可以参考 矩阵求导术，当然我又是在挖坑了🤣，以后再来整理吧！

数值稳定性和模型初始化

在 MLP 的模型下，加入所有隐藏变量和输入都是向量，那么求解其中任一参数 W 的梯度将面临如下的过程（注意下面表达式 $W^t$ 其实不需要转置）

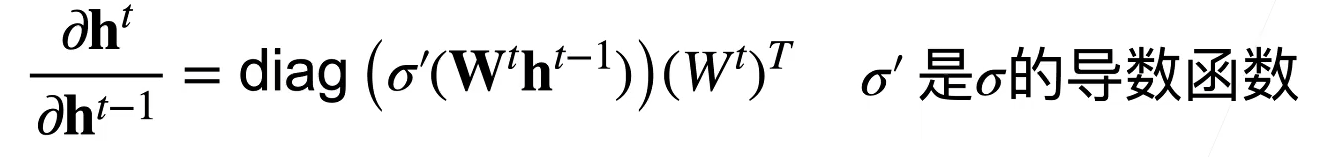
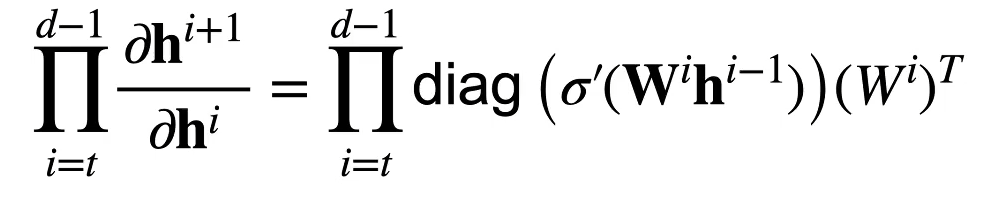
也就是说会有多个矩阵进行连续的相乘，如果没有一个很好的初始化，那么我们将会面临梯度爆炸或者梯度消失的情况。当然这也跟激活函数相关，ReLU 的设计将减缓部分梯度消失情况

参数初始化

初始参数过大、过小会引起梯度爆炸/消失，初始参数全部取相同值也会导致优化时所有参数更新的值都是一样的（MLP 模型下）

使用正态分布来初始化权重值，对于中等规模的问题通常很有效。教材还介绍了另一种初始化方法 Xavier 初始化，可以参考 知乎

环境和分布偏移

机器学习的许多应用中都存在类似的问题：通过将基于模型的决策引入环境，我们可能会破坏模型

分布偏移的类型

协变量偏移

在分布偏移的分类中，协变量偏移可能是研究的最广泛的。这里我们假设，虽然输入的分布可能随时间而改变，但标签函数，即条件分布 $P(y∣x)$ 没有改变。教材举了一个猫狗的例子

测试时的数据相比训练时发生了变化，但是标签的并没有改变

标签偏移

标签偏移描述了与协变量偏移相反的问题。标签边缘概率 $P(y)$ 可以改变，但是类别条件分布 $P(x∣y)$ 在不同的领域之间保持不变。简单的理解就是样本标签/类别不均衡的问题

概念偏移

当标签的定义发生变化时，就会出现这种问题，通俗一点说是说我们可以指猫为”狗“。从数学上来说，是输入的边缘分布相同，标签的边缘分布也相同：$p_s(x)=p_t(x),p_s(y)=p_t(y)$，但是条件分布不同：$p_s(y|x)≠p_t(y|x)$

分布偏移纠正

主要是通过纠正损失函数的偏移来解决这个问题，具体来说就是给损失函数加权，这就要使用测试集中的样本分布了。而且教材也提到：不耐烦的读者可以继续下一节，因为这些内容不是后续概念的先修内容，而我就是不耐烦的那一批😁

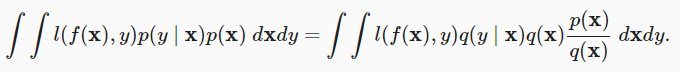
机器学习中的公平、责任和透明度

这部分讲了一些道德伦理困境。教材原文：通常，在建模纠正过程中，模型的预测与训练数据耦合的各种机制都没有得到解释。这可能导致研究人员称之为“失控反馈循环”的现象

就像一个正反馈机制一样，比如在一个推荐系统中，你会被推荐越来越多相似的内容；而在一个犯罪预警系统中，某一个社区或者某一类人将会被越来越针对