D2L 03 线性神经网络

在本章中，我们将介绍神经网络的整个训练过程，包括：定义简单的神经网络架构、数据处理、指定损失函数和如何训练模型

经典统计学习技术中的线性回归和softmax回归可以视为线性神经网络

线性回归

几个基本的概念

• 数据集 $X \in \mathbb R^{n\times d}$
• 样本，特征/协变量
• 标签/目标 $y \in R^n$

线性模型

使用仿射变换得到预测值 $\hat{\bold y}$

$$\hat{\bold y} = \bold X\bold w+b$$

$\bold w\in R^d$，$b$ 是一个标量

损失函数

MSE（Mean Square Error）

$$L(\mathbf{w}, b)=\frac{1}{n} \sum_{i=1}^{n} l^{(i)}(\mathbf{w}, b)=\frac{1}{n} \sum_{i=1}^{n} \frac{1}{2}\left(\mathbf{w}^{\top} \mathbf{x}^{(i)}+b-y^{(i)}\right)^{2}$$

希望寻找一组参数使得损失函数最小

$$\mathbf{w}^{*}, b^{*}=\underset{\mathbf{w}, b}{\operatorname{argmin}} L(\mathbf{w}, b)$$

简单的线性问题可以有解析解，但一般深度学习的问题中很难找到解析解

梯度下降

小批量随机梯度下降

学到这里，我已经感受到大部分深度学习教材的数学都没有进行深入的挖掘，其核心在于”动手”，通过简单的叙述和代码，让人们入门深度学习，有一个整体的认识，知道深度学习能够干什么

但是真正的深入：概率论，信息论，线性代数（矩阵求导），机器学习等所有的核心知识，都有所欠缺，所以现在改变策略，将不进行细致的整理，仅记录我认为有用的部分，并进行适当扩充。主要目的为编程练习

正态分布与平方损失

在高斯噪声的假设下，最小化均方误差等价于对线性模型的最大似然估计

线性回归 pytorch 实现

import numpy as np
import torch
from torch.utils import data

# 定义随机种子
np.random.seed(1)
torch.manual_seed(1)

def synthetic_data(w, b, num_examples):
    X = np.random.normal(0, 1, (num_examples, len(w)))
    y = np.dot(X, w) + b
    y += np.random.normal(0, 0.01, y.shape)
    X, y = torch.from_numpy(X).float(), torch.from_numpy(y).to(torch.float32)
    return X, y.reshape((-1, 1))

true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = synthetic_data(true_w, true_b, 1000)

# 读取数据集
def load_array(data_arrays, batch_size, is_train=True):  #@save
    """构造一个PyTorch数据迭代器。"""
    dataset = data.TensorDataset(*data_arrays)
    return data.DataLoader(dataset, batch_size, shuffle=is_train)

batch_size = 10
data_iter = load_array((features, labels), batch_size)

# 定义模型
from torch import nn

net = nn.Sequential(nn.Linear(2, 1))

# 初始化参数
net[0].weight.data.normal_(0, 0.01)
net[0].bias.data.fill_(0)

# 定义损失函数
loss = nn.MSELoss()

# 定义优化算法
trainer = torch.optim.SGD(net.parameters(), lr=0.03)

# 训练
num_epochs = 3
for epoch in range(num_epochs):
    for X, y in data_iter:
        l = loss(net(X) ,y)
        trainer.zero_grad()
        l.backward()
        trainer.step()
    l = loss(net(features), labels)
    print(f'epoch {epoch + 1}, loss {l:f}')

学习点：

1. torch.Tensor.to(torch.float32) doc 既可以转换类型，又可以转换 cpu/gpu 设备

2. 可以通过序号 net[idx].weight 访问 nn.Sequential 中指定网络层的参数

3. 关于 torch.nn

Softmax 回归

One-hot 编码

编码是一个向量，它的分量和类别一样多。类别对应的分量设置为1，其他所有分量设置为0

Softmax 运算

假设有一个样本，输入为 o，分类数量为 q，预测值为 y

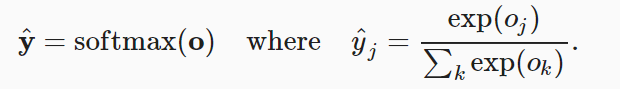
尽管 softmax 是一个非线性函数，但 softmax 回归的输出仍然由输入特征的仿射变换决定。因此，softmax 回归是一个线性模型

损失函数

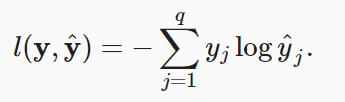
以上为似然函数，也被常称为（多分类）交叉熵损失。交叉熵是一个衡量两个概率分布之间差异的很好的度量。它测量给定模型编码数据所需的比特数

Softmax 及其导数

将 softmax 的公式带入到损失函数中并求导

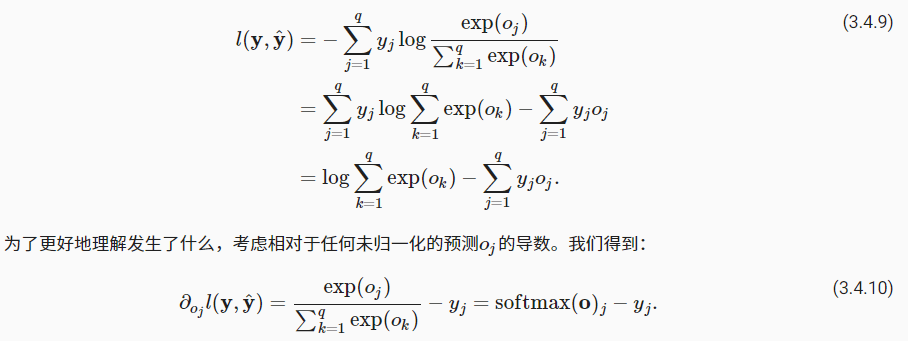
导数是我们模型分配的概率（由 softmax 得到）与实际发生的情况（由独热标签向量表示）之间的差异。从这个意义上讲，与我们在回归中看到的非常相似

Fashion-MNIST 数据集

这一小节介绍了如何从 pytorch api 加载该数据集

Softmax Pytorch 实现

上溢下溢问题

如何解决 exp 上溢和 log 下溢问题？

1. softmax 上下同时除以 exp(max(x)) 可以解决上溢问题。但当 exp(max(x)) 比较大 (>1000) 时，softmax 会直接返回 0，再进入 log 函数就会产生下溢
2. 解决方法是直接输入 logits 输出交叉熵，即不经过 softmax 运算。因为 log 和 exp 是一对反函数，它们可以相互抵消，log(exp(x)) = x

import torch
from torch import nn
from torch.utils.data.dataloader import DataLoader
from torch.utils.data.sampler import SubsetRandomSampler
from  torchvision import datasets
from torch.optim import SGD

from torchvision.transforms import ToTensor
import time

training_data = datasets.FashionMNIST(
    root="./data",
    train=True,
    download=True,
    transform=ToTensor()
)

test_data = datasets.FashionMNIST(
    root="./data",
    train=False,
    download=True,
    transform=ToTensor()
)

device = torch.device('cuda')
batch_size = 256
NUM_TRAIN = 1000
sampler = SubsetRandomSampler(range(NUM_TRAIN))

# 暂时先不用 sampler
train_loader = DataLoader(training_data, batch_size=batch_size)

# PyTorch不会隐式地调整输入的形状。因此，
# 我们在线性层前定义了展平层（flatten），来调整网络输入的形状
net = nn.Sequential(nn.Flatten(), nn.Linear(784, 10))
net.to(device)

def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, std=0.01)

net.apply(init_weights);

# 损失函数并移动到 GPU
# input is logits, i.e. raw scores
loss = nn.CrossEntropyLoss()
loss.to(device)

optim = SGD(net.parameters(), lr=0.01)


def eval(output: torch.Tensor, label: torch.Tensor):
    pred = output.argmax(dim=-1)
    acc_num = (pred.to(label.dtype) == label).sum()
    return acc_num 


def train(model: nn.Module, train_loader, epochs, optim: SGD, loss_fn):
    model.train()
    for epoch in range(epochs):
        start = time.time()
        loss = 0
        acc_num = 0
        for data, label in train_loader:
            # 将 data 移入 GPU
            data = data.to(device)
            label = label.to(device)
            output = model(data)
            loss = loss_fn(output, label)
            optim.zero_grad()
            loss.backward()
            optim.step()
            acc_num += eval(output, label)
        print(f'epoch: {epoch}, loss: {loss:.4f}, train_acc: {acc_num / len(training_data):.2f}, time:{time.time() -start:.2f}')

train(net, train_loader, epochs=80, optim=optim, loss_fn=loss)

自己写一个 softmax 实现，最终结果与官方差不多，以下结果来自自己，图像来自官方

epoch: 0, loss: 0.983296, train_acc: 0.64, time:4.58
epoch: 1, loss: 0.797371, train_acc: 0.72, time:4.47
epoch: 2, loss: 0.712272, train_acc: 0.75, time:4.44
epoch: 3, loss: 0.660301, train_acc: 0.77, time:4.40
epoch: 4, loss: 0.624506, train_acc: 0.78, time:4.49
epoch: 5, loss: 0.598148, train_acc: 0.79, time:4.52
epoch: 6, loss: 0.577858, train_acc: 0.80, time:4.58
epoch: 7, loss: 0.561719, train_acc: 0.80, time:4.59
epoch: 8, loss: 0.548546, train_acc: 0.80, time:4.45
epoch: 9, loss: 0.537567, train_acc: 0.81, time:4.43
epoch: 10, loss: 0.528253, train_acc: 0.81, time:4.50

学习点：

1. 在实现过程中发现了 add_module 的作用，相当于在 __init__ 中使用了 self.module_name = nn.xxx，即把一个模块注册到当前模型中，成为该模型的 children / 子模块。在之后的训练中将会更新这个模块的参数，并且该模块也能作为属性被模型访问 model.module_name
2. 通过 nn.init 模块可以对模型参数进行初始化
3. 通过 nn.apply(fn) 循环地对所有子模型 model.children() 进行操作
4. 需要将模型和数据都转移到相同的设备上才能进行运算，如果损失函数也是 nn.Module 的子类，则也需要转移

补充：为什么使用 CE 进行分类而不使用 MSE

1. 从梯度角度来看。分类问题的输出通常经过 sigmoid or softmax 函数，以 sigmoid 函数为例，函数的两端会非常非常的平缓，这就会导致梯度消失，网络无法进一步优化

2. 交叉熵就是用于衡量两个分布之间的相似度。这里又要提一句 KL 散度和交叉熵之间的关系与区别：KL 散度可以被用于计算两个分布的差异，而在特定情况下最小化 KL 散度等价于最小化交叉熵。而交叉熵的运算更简单，所以用交叉熵来当做代价。再贴几个公式

   $$S(v)=-\sum_{i} p\left(v_{i}\right) \log p\left(v_{i}\right) \\ D_{K L}(A \| B)=\sum_{i} p_{A}\left(v_{i}\right) \log p_{A}\left(v_{i}\right)-p_{A}\left(v_{i}\right) \log p_{B}\left(v_{i}\right) \\ H(A, B)=-\sum_{i} p_{A}\left(v_{i}\right) \log p_{B}\left(v_{i}\right) \\ H(A, B)=D_{K L}(A \| B)+S_{A}$$

   当 $S_A$ 为常数时，优化交叉熵等价于优化 KL 散度。最后提一句通过 Jensen 不等式可证明 KL 散度大于0