PointNet & PointNet++
Qi, Charles R., Hao Su, Kaichun Mo, and Leonidas J. Guibas. “PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation.” ArXiv:1612.00593 [Cs], April 10, 2017. http://arxiv.org/abs/1612.00593.
Comment: CVPR 2017
Qi, Charles R., Li Yi, Hao Su, and Leonidas J. Guibas. “PointNet++: Deep Hierarchical Feature Learning on Point Sets in a Metric Space.” ArXiv:1706.02413 [Cs], June 7, 2017. http://arxiv.org/abs/1706.02413.
From zotero
PointNet 算是利用深度学习处理点云数据的开山之作。由于点云数据对比图片数据更加混乱和复杂,原有的二维处理方法面对点云数据并没有起到好的效果,但在 PointNet 提出后,处理三维点云数据有了新的思路,并且实验结果有了显著的提升。该笔记主要为了总结 PointNet 和 PointNet++ 中心思想,参考链接:CSDN
PointNet
三维表示

三维数据的表述形式一般分为四种:
点云:由 N 个 D 维的点组成,当这个 D = 3 的时候一般代表着 $(x, y, z)$ 的坐标,当然也可以包括一些法向量、强度等别的特征
Mesh:由三角面片和正方形面片组成
体素:由三维栅格将物体用0和1表征
多角度的RGB图像或者RGB-D图像
为什么使用点云数据?
- 点云更接近于设备的原始表征(即雷达扫描物体直接产生点云)
- 点云的表达方式更加简单,一个物体仅用一个 N × D 的矩阵表示
Properties of Point Sets
- Unordered,无序性
- Interaction among points,点与点之间的作用
- Invariance under transformations,空间不变性
以上性质的前两点是区别于二维图像数据的,也是处理点云数据的难点。PointNet 核心的贡献有两点,一个是解决无序的点云输入,一个是解决空间不变性。但是对于处理空间不变性的结构,在现在看来似乎没有必要性。而且对于点与点之间的作用 PointNet 也没有深入考虑,但在之后的 PointNet++ 中提出了解决方法
PointNet Architecture
先看下图有个整体感受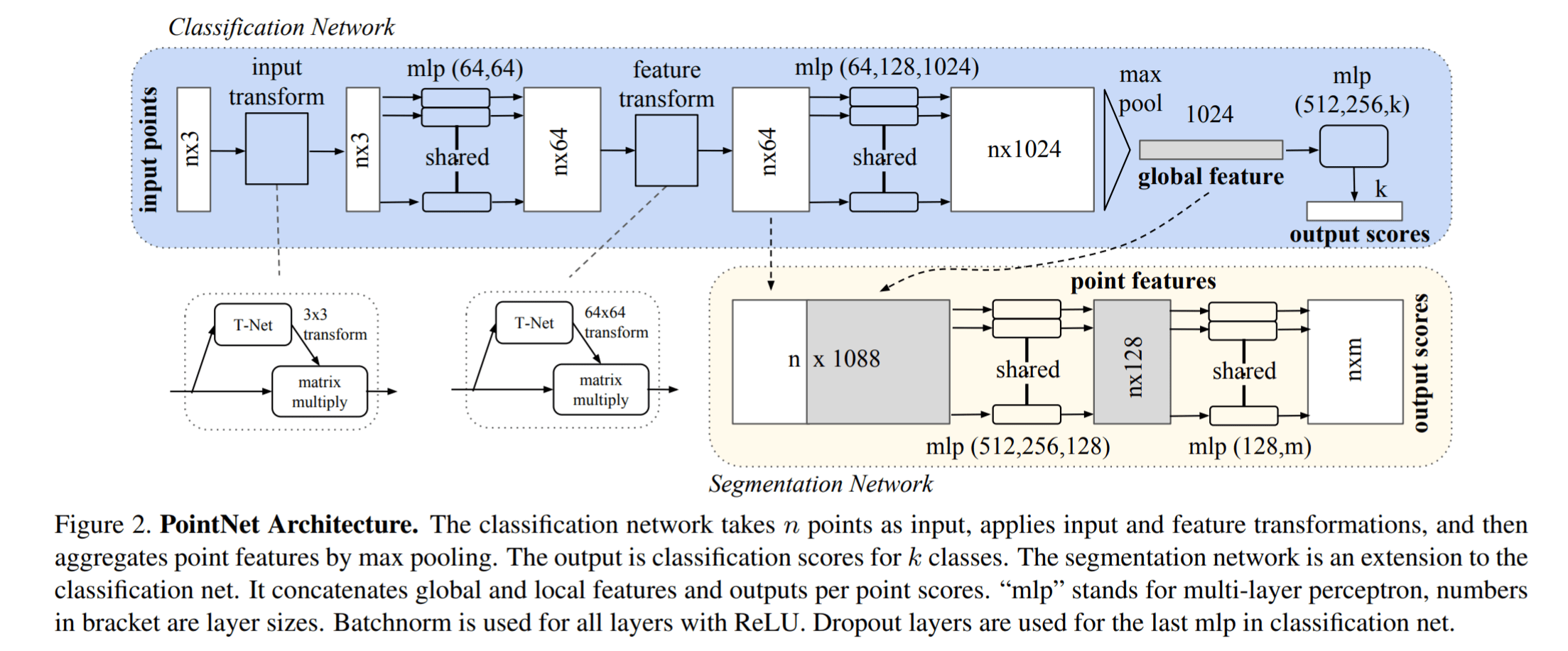
PointNet 能够处理分类任务和分割任务,分别对应着流程图的上下两个部分
input transform 和 feature transform 的设计初衷是为了让网络面对空间的旋转、缩放等有一定的鲁棒性,在论文中的方法是新引入了一个 T-Net 网络去学习点云的旋转,将物体校准,具体的结构在该笔记中不会详细介绍
Shared MLP 本质为一维的卷积 Conv1d,可以参考链接 CSDN 进一步学习。Shared MLP + Max Pooling 操作实现了对无序性点云数据的对称处理,即当点云输入顺序改变时,输出结果不会因为输入顺序的改变而改变。注意 Max Pooling 是对不同的点而言的,而不是对于同一个点的特征向量操作的。下面我们将重点讨论为何使用 Shared MLP + Max Pooling
Symmetry Function for Unordered Input
点云实际上拥有置换不变性的特点,那么什么是置换不变性呢,简单地说就是点的排序不影响物体的性质。因此针对点云的置换不变性,其设计的网络必须是一个对称的函数,我们经常看到的 sum 和 max 等函数其实都是对称函数
文章的具体做法为:将点云数据使用 Shared MLP 升维(从3维最终升至1024维),然后使用 max pooling 操作,得到一个全局的特征向量 global feature。使用该 global feature 就可以进行点云的分类任务了,而如果是进行点云分割任务,则需要和每个点的局部特征结合起来,再进行计算
Q:升维(或者说多卷积核)在深度学习当中是非常常见的,该操作的本质意义是什么?个人猜测:对高维度的空间进行分割更简单,并对数据保留足够的特征
Shared MLP + Max Pooling 的合理性
该论文提出了如下的定理,该定理基于万能近似定理(Universal Approximate Theorem)

对于文章证明理解,有2个概念需要进一步了解,一个是 Hausdorff_distance 一个是 Power set,前者表示了两个集合的距离,后者表示了一个集合的所有子集
该定理的结论是,论文提出的结构,能够拟合任意的连续集合函数。这个定理的结论,并没有什么特殊意义,因为万能近似定理告诉我们,足够多节点的 MLP 能够近似任何连续函数。重点在于论文的证明过程,给出了 Shared MLP + Max Pooling 的合理性,该合理性总结为如下
The proof to this theorem can be found in our supplementary material. The key idea is that in the worst case the network can learn to convert a point cloud into a volumetric representation, by partitioning the space into equal-sized voxels. In practice, however, the network learns a much smarter strategy to probe the space, as we shall see in point function visualizations.
这里的 worst case 的“最差”体现在何处我并不理解,但是证明过程中指出了网络的一条可能的学习路径。该学习路径描述为如下:
- 将所有的点映射到其“附近”的栅格点中,这样得到一个新的点集,可以证明使用该栅格点集作为输入去替换原点集,并不会对输出造成太大的影响,所以该栅格点集就是对原点集的一个很好的近似。而这个映射就是由 Shared MLP + Max Pooling + MLP 完成
- 此时还需要使用新的 MLP 完成对原连续集函数的拟合。该 MLP 和第一步中的 MLP 可以叠加起来,作为一个整体的 MLP,在公式中即表示为 γ 函数
通过人为设置的学习路径,解释了该结构的合理性。但通过网络自身的学习,能够获得更好的效果,剩下的就交给优化算法吧!
更新:从升维的角度来看待 PointNet
为什么要将每一个点的位置使用全连接网络进行升维度?BTW,因为每一个点都共用一个全连接网络所以叫 shared MLP
这样的升维操作我在 one-hot 编码中看到过,即用一个多维的,由 {0,1} 组成的向量来表示属于某一个类,这里会不会是相同的道理?MLP 的权重实际上是空间中的多个向量,这些向量将空间分割成多个子空间,如果输入向量落在该子空间中,则输入向量与分隔向量的点积数值就会较大,此时可以把则该子空间看作为某种特征。之后使用 maxpooling 堆所有输入向量进行全局的特征提取,最后使用 MLP 进行各种下游任务
这个思想(可能)起源于传统的滤波,也可能来自于看了马毅教授的一些说法:把滤波/卷积核看作是一个高维度向量,而卷积操作实际上是该部分数据与该向量的点积,也就是在该方向上的投影,寻找卷积核就是在寻找不同的高维向量,对高维空间进行分割,原始特征落在高维空间的不同区域,它们与高维向量的点积代表了它们在这些方向上的投影,如果方向相同那么投影值肯定会打,如果方向垂直或者相反投影值则会变小,这样落在不同区域的特征将会被识别出来(通过 ReLU or maxpooling),这些投影值可能就是我们常说的提取得到的“特征”
PointNet++
PointNet++ 的提出源于 PointNet 的缺点——缺失局部特征。PointNet对于场景的分割效果十分一般,由于其网络直接暴力地将所有的点最大池化为了一个全局特征,因此局部点与点之间的联系并没有被网络学习到。PointNet++ 中主要借鉴了 CNN 的多层感受野的思想,增强了网络对于局部特征的提取能力
具体来讲就是:对于点云数据,将点云数据进行采样和分组,使用原 PointNet 对这些分组后的点云子集进行特征提取(而非之前的全局特征提取),得到了新的特征集合,对于新的特征集合,可以重复之前的采样、分组、提取过程,不断地迭代。随着迭代次数的增加,PointNet 的感受野也越来越大,下图为 PointNet++ (single scale grouping) 的结构图,能够有一个更加直观的感受
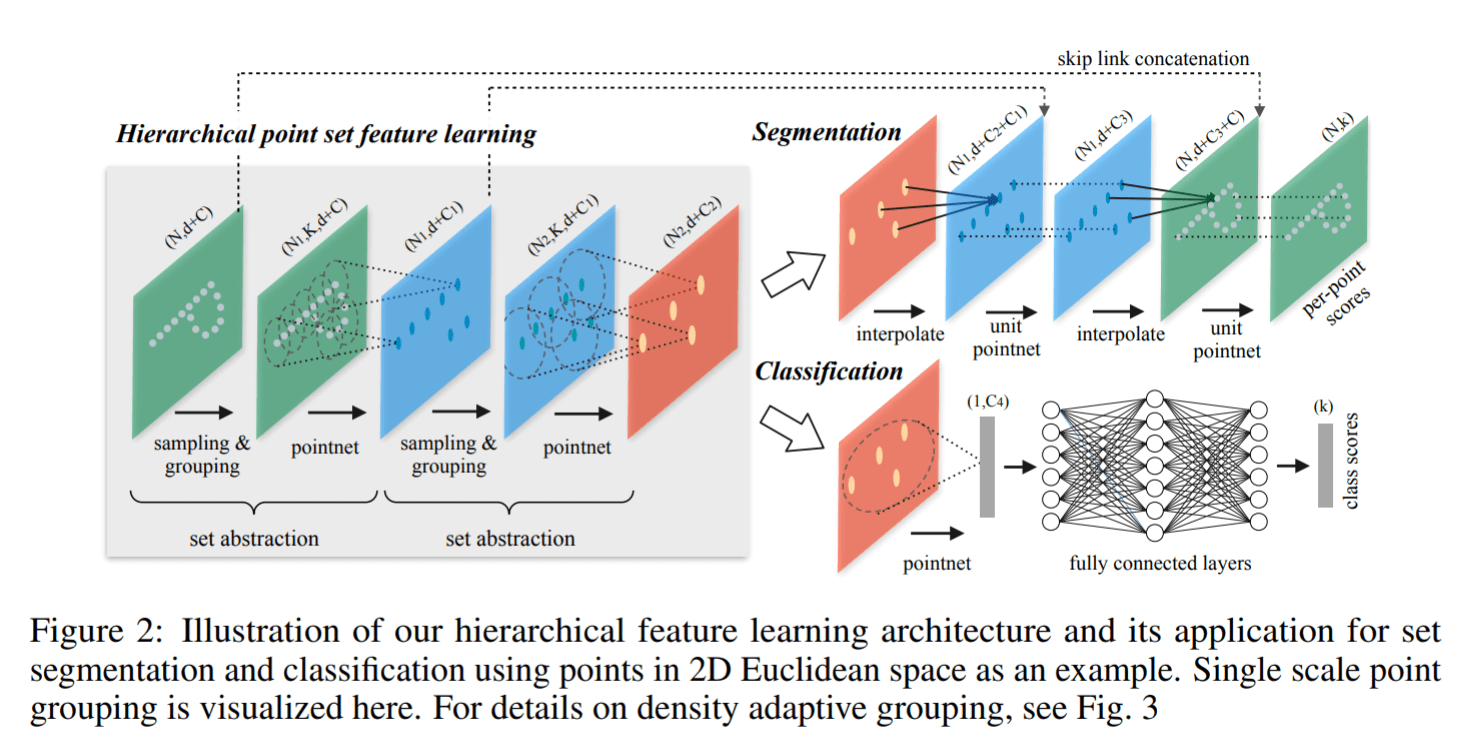
PointNet++ Architecture
和 PointNet 类似,整体依旧是 encoder-decoder 模式,可以处理分割任务和分类任务,但两个任务的 decoder 不相同
Encoder
Encoder 由多个 set abstraction 结构组成,其中 set abstraction 由3个重要部分组成:sampling 采样,grouping 分组,PointNet 使用 PointNet 采集特征,接下来进一步了解这三个部分
- Sampling:使用利用 FPS(最远点采样)随机采样点,参考链接 CSDN
- Grouping:利用 Ball Query 划一个 R 为半径的圈,将每个圈里面的点云作为一簇
- PointNet: 对 Sampling + Grouping 以后的点云进行特征提取,注意这里的 PointNet 和原 PointNet 相比,去掉了其中的 T-Net transform 的部分
数据的形状变化为:
Input (N, d) -> sampling (n, d) -> grouping (n, K, d) -> PointNet (n, C + d) -> …
其中 d 应该为点的原始信息,会一直跟随着点存在,因为 sampling + grouping 将会使用
Decoder
分类任务的 decoder 也是比较简单,直接使用 PointNet 提取全局特征,然后送入 MLP 中进行分类
分割任务的 decoder 需要得到每一个点的特征向量,但是经过 encoder 我们只有少数一些点的特征,应该怎么办呢?论文采取的结构为 Point Feature Propagation,将少数点的特征逐层传播到每一个点,其本质为插值 interpolation。公式如下,由 latexlive 从图片生成
简单来说,就是将该点周围的点的特征值进行加权平均,作为该点自己的特征,论文取 k = 3, p = 2,即 neighbor 有3个,距离为欧氏距离
除了对点进行插值,进行特征传播外,论文还将插值得到特征与 encoder 中对应层的相同点的特征连接起来 concatenate,使得特征的信息保留更多
多尺度 MSG & MRG
为了继续增加网络对于多尺度信息的提取,论文也提出了两种多尺度 grouping 方法,MSG & MRG 如下图所示
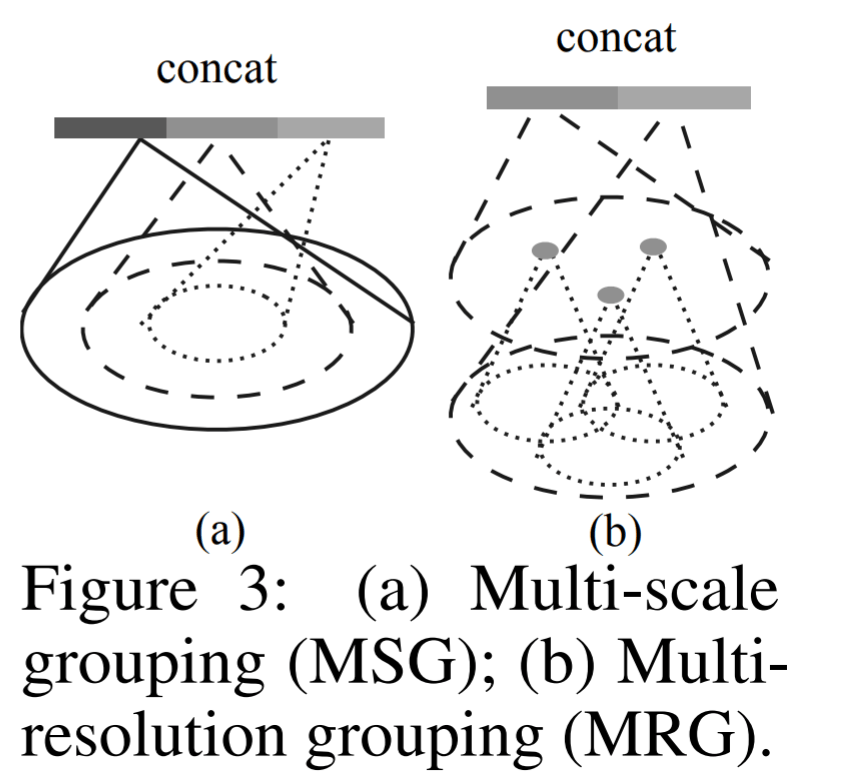
- MSG:比较好理解,就是使用多个半径,去获取多个尺度的特征,然后将这些特征连接起来
- MRG:MSG 的计算量相对比较大,尤其是在点比较多的时候。论文提出了 MRG,MRG 分为两个部分,左边特征为一般的 grouping 得到的特征,右边特征为该 grouping 范围在原始点云中的位置,对该位置范围内的原始点云做特征提取。由于 MRG 作者并为将其代码开源,所以可能理解并不深刻,所以请参考原文及其附录
数据预处理 Dropout
多尺度训练的目的之一是为了更好应对点云密度的变化,对于密度低的点云,选取更大尺度范围的特征效果会更好。同时论文也采用了 dropout 操作,对训练数据点以 dropout ratio θ 进行随机剔除,而 θ 是从 0-0.95 中均匀采样得到,这样就能创建不同密度的点云数据了
总结
PointNet 系列是点云分割网络最初的 baseline,一些网络也是通过以这两个网络为基础构造出来的。其优点非常的明显,就是参数量小;但其缺点就是对于局部的特征的抓取还不是特别的完善,这也是未来可以改进的地方